Accepted: November 17, 2018 | Published Online: November 19, 2018

Citation: Zakrzhevskii A (2018) Feed-forward Control Based on a Neural Network Technology for an Optimal Slewing of the Flexible Spacecraft. Int J Astronaut Aeronautical Eng 3:018.

Copyright: © 2018 Zakrzhevskii A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Abstract

The problem of construction of optimal program slewing of spacecraft with attached flexible elements in the class of slewing around Eulerian axis is considered. The mathematical model is developed, allowing considering a finite number of natural modes of flexible vibrations. The problem of optimal reorientation of spacecraft with nontraditional objective of control, reducing to a minimum dynamic overload of flexible elements in a relative motion is formulated. The algorithm of numerical solving of the corresponding nonlinear boundary problem, realized in the form of a package of applied programs in FORTRAN is developed. The network whose training can be made during of preflight preparation is created in space of the slewing parameters. Simulation of fast calculation of the parameters of the optimal slewing program in flight is made on the basis of use of known radial basic functions.

Introduction

Recently interest to motion control of flexible spacecraft (SC) round the mass center, in particular, to a mode of their optimal reorientation, has been increased. It is caused by necessity of creation of a new generation of lightweight flexible SC of different function, capable to expedite reorientation modes, without exciting at that flexible oscillations of their structures. Within the last decade, development of the new concept in the modeling, analysis, and control for such SC goes in two main directions. On the one hand, in their constructions the distributed actuators of a control system and the smart composite materials are more widely used expanding possibilities of the distributed actuators [1]. On the other hand, extend researches in the field of creation of so-called neural networks, allowing accumulating the information in nodes of such networks during the preflight period and with split-hair accuracy to recover control laws in an orbit for current terminal conditions [2,3]. In practice, control of such systems uses a combination of feedforward and feedback control. Some measurements of the deformation of flexible appendages are possible only when distributed sensors are used. The performance of the feedback is limited, if a spacecraft has not such sensors. As a result, the feedforward control, which takes proper account of the object's dynamic properties, is of great importance for this problem.

At that, it is not necessary to resort to the solution of a problem of the optimal control in an orbit demanding sometimes enough durable calculations even on the modern computers. Approximation of the vectorial fields determining program (feedforward) laws of control based on a method of neural networks demands essentially less of mathematical operations and can be realized on more simple on-board computers.

Both for absolutely rigid, and for flexible SC the reorientation mode can be carried out by:

• Three serial rotations on certain angles round the axes fixed in a unstrained main module;

• Two serial rotations, if the antenna is guided with SC main module and it is not used for radiation or reception of a polarized signal, and when the antenna is oriented separately;

• One rotation about an axis of the equivalent rotation (Euler's axis), fixed in the inertial space and fixed in the SC;

• Process optimization of a flexible SC slewing can have the various objectives;

• For durably existing SC with the weak installed power per employee, functioning with breaks, objective is more often to minimize energy expenses to the detriment of high-speed performance;

• For SC, related to astronomical observations (EINSTEIN, GAMMA, HUBBLE, SAX, etc.), fulfilling a considerable number of maneuvers during their functioning when they cannot fulfill observation, remains important convergence of duration of the maneuver to a minimum [4,5];

• For the SC having very large flexible structures it is very important to minimize flexible deformations during the whole maneuver [6];

For the active suppression of excited flexible oscillations the additional actuators of a control system creating both internal and external control actions are needed. When they are absent, the problem demands the setting of new problems of the maneuver optimization.

The first attempts to formulate the objective function, which takes into account design elastic properties, were made in the seventies. The author [6-8] used a quadratic objective function, the physical meaning of which was to minimize the relative acceleration of the flexible elements during the controlled motion. Farrenkopf [9] used a quadratic criterion including in the cost function formally the terminal values and the mean values of the generalized elastic coordinates and their first and second derivatives on the control time interval. Other older investigations in this area included a number of approaches developed for linear flexible systems, which shape the feedforward input such that it does not contain spectral components at system eigenfrequencies [10]. Modifications of such methods have been applied to nonlinear flexible systems [11], but they may yield a significant level of residual vibrations [12].

Here the problem of creation of the optimal program slewing of SC with attached flexible elements is considered in a class of slewing around Euler's axis with unconventional objective function.

The mathematical model is developed, allowing considering the finite amount of natural modes of flexible oscillations. The problem of the optimal SC reorientation with unconventional objective function, reducing dynamic overloads of flexible elements to minimum in the relative motion is formulated. The algorithm of the numerical solving of the appropriate non-linear boundary value problem (BVP), implemented in the application program package in language FORTRAN is developed. The neural network is created in the space of slewing parameters, whose training can be led in the preflight period. Process of simulation of fast calculations in flight of the parameters of the program of optimal reorientation is led based on known radial basis functions.

Problem Formulation

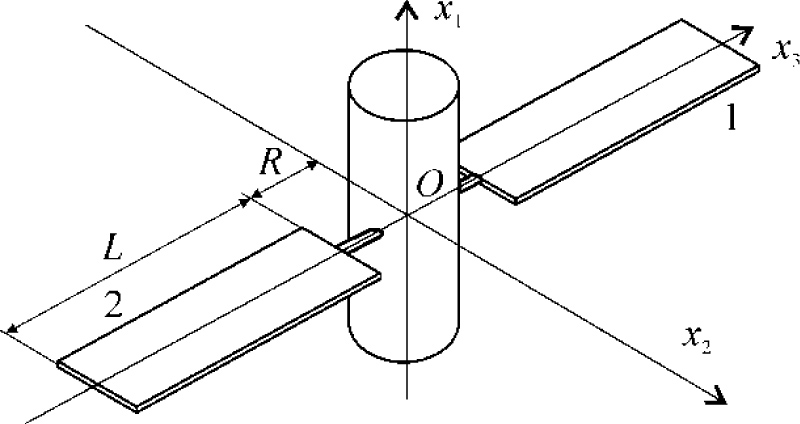
We consider SC (Figure 1), consisting of the rigid main module and two flexible panels of solar batteries symmetrically attached to it. Assume presence of sensors of angles of orientation and angular velocities at the main module, the on-board computer, capable to form control laws according to the given algorithms, and control system actuators, such as three flywheels with axes of rotation directed along the principal axes of inertia $O{x}_1{x}_2{x}_3$ of the strainless object (connected frame of reference).

Let us introduce fixed in the inertial space the frames of reference $O{x}_1^0{x}_2^0{x}_3^0$ and $O{x}_1^f{x}_2^f{x}_3^f$, coinciding with $O{x}_1{x}_2{x}_3$ in the beginning and in the end of a slewing accordingly. We introduce also the frame of reference $O{\xi }_1{\xi }_2{\xi }_3$, fixed in the main module and coinciding in the beginning of a slewing with the reference frame $O{\xi }_1^0{\xi }_2^0{\xi }_3^0$, in such a way that axes $O{\xi }_1$ and $O{\xi }_1^0$ coincide with Euler's axis. For this frame of reference, we introduce the system of basis unit vectors. Basis vectors $i_k$ correspond to axes $O{x}_k$, $i_k^f-O{x}_k^f$, $e_k-O{\xi }_k$, $e_k^0-O{\xi }_k^0$, $i_k^f-O{x}_k^f$, $\left(k=1,2,3\right)$. Transfer from one frame of reference to another we define as

$i_k={\displaystyle \sum _{j=1}^3{c}_{kj}}{i}_j^0$, $e_k^0={\displaystyle \sum _{m=1}^3{\gamma }_{km}}{i}_m^0$, $e_k={\displaystyle \sum _{m=1}^3{\gamma }_{km}}{i}_k={\displaystyle \sum _{m=1}^3{b}_{km}}{e}_m^0$, $i_k^j={\displaystyle \sum _{m=1}^3{a}_{km}}{i}_m^0$

Matrix $\Vert a\Vert$ is defined by the given angles of rotations around the connected axes and allows to define value of an angle of a finite rotation $\Psi$ round $O{\xi }_1$ axis and directing cosines ${\gamma }_{1i}$ of $O{\xi }_1$ axis in the frame of reference $\text{O}{x}_i^0\left(i\text{ = 1,2,3}\right)$. Remaining components of the matrix $\Vert \gamma \Vert$ can be selected arbitrarily, proceeding from a condition that $e_i\left(i=1,2,3\right)$ form the right hand triple of mutually orthogonal vectors. The matrix

$\Vert b\Vert$ has a form: $\Vert b\Vert =\Vert \begin{array}{ccc}1& 0& 0\\ 0& \cos \psi & \sin \psi \\ 0& -\sin \psi & \cos \psi \end{array}\Vert$,

where $\psi \left(t\right)$ is the angle of rotation of the reference frame $O{\xi }_k$ about $O{\xi }_1$ axis. As a result:

$$c_{ki}={\displaystyle \sum _{p=1}^3{\displaystyle \sum _{q=1}^3{\gamma }_{pk}{b}_{pq}}}{\gamma }_{ql},\left(k,l=1,2,3\right)\text{ (1)}$$

I.e. the directing cosines of the connected frame of reference can be defined in the basis (1) as functions of the angle $\psi \left(t\right)$. The vector of the angular velocity of a main module coincides with $O{\xi }_1$ axis, i.e.

$${\omega }_i\text{ = }\dot{\psi }(t){\gamma }_{1i}\left(i\text{ = 1,2,3}\right)\text{ (2)}$$

For description of motion of flexible elements we use the discrete finite-dimensional model [2]. The questions related to creation of such models for continual systems are widely illuminated in the literature. We select such a model enough simple for the mathematical description and at the same time allowing us to show possibilities of optimization of control of a three-dimensional slewing as active protection of flexible elements from dynamic overloads.

Let us assume that the pattern of deformations of flexible elements is axisymmetric with respect to Ox₂ axis. Then the instant position of the mass center of all system coincides with a pole O.

The equations of motion of flexible elements of the object can be written in a form:

$${\ddot{q}}_{\alpha }+2n_{\alpha }{\dot{q}}_{\alpha }+\left({\Omega }_{\alpha }{}^2-{\omega }_2^2-{\omega }_3^2\right)q_{\alpha }\text{ = }{R}_{\alpha }\left({\dot{\omega }}_2+{\omega }_1{\omega }_3\right)\text{ (3)}$$

Where $R_{\alpha }=2{{\displaystyle \underset{m}{\int }\overrightarrow{U}}}^{\alpha }\times \overrightarrow{\rho }dm/{{\displaystyle \underset{m}{\int }\overrightarrow{U}}}^{\alpha }\times {\overrightarrow{U}}^{\alpha }dm$, ${\overrightarrow{U}}^{\alpha }={\overrightarrow{i}}_1{\phi }_{\alpha }\left(x_3\right)$, $\left(\alpha \text{ = 1,}\mathrm{...}\text{,}N\right)$, ${\phi }_{\alpha }\left(x_3\right)$ are natural modes of the flexible console.

Here:

$q_{\alpha }$ is the generalized coordinates corresponding to axisymmetric deviation of flexible elements 1 and 2 (Figure 1);

$n_{\alpha }$ are the generalized coefficients of structural damping;

${\Omega }_{\alpha }$ are natural frequencies of flexible oscillations;

N is a number of considered modes of oscillations.

The remaining ODEs defining the SC dynamics can be omitted, since the attitude of the main body is defined completely by the law $\psi \left(t\right)$ of its rotations around Eulerian axis and three directing cosines of $O{\xi }_1$ axis in the frame of reference $O{x}_1^0{x}_2^0{x}_3^0$.

The Optimal Control Objective Function

We consider the following objective of optimal control: To find the law of control for a slew of the SC around an Eulerian axis on the prescribed angle $\Psi$ during given time at which the boundary conditions for phase variables are satisfied and the relative dynamic overloads of flexible elements are minimized during the slewing.

Let us present a vector of flexible displacement in the form:

$\overrightarrow{\text{w}}\text{ = }{\displaystyle \sum _{\text{α = 1}}^{\text{N}}{\text{q}}_{\text{α}}\text{(t)}}{\overrightarrow{\text{W}}}_{\text{α}}{\text{(x}}_{\text{3}}\text{)}$

Here ${\overrightarrow{W}}_{\alpha }=-{\overrightarrow{U}}^{\alpha }$ in the area occupied by element 1 and ${\overrightarrow{W}}_{\alpha }={\overrightarrow{U}}^{\alpha }$ for an element 2. Then for minimization of the specified dynamic overloads the objective function of the control can be selected in the form:

$$\text{J = }\frac{\text{1}}{\text{2}}{\displaystyle \underset{\text{0}}{\overset{\text{T}}{\int }}{\displaystyle \underset{\text{m}}{\int }{\text{(}\stackrel{\mathrm{..}}{\text{w}}\text{)}}^{\text{2}}\text{dm}\text{dt }}\text{= }\frac{\text{1}}{\text{2}}}{\displaystyle \underset{\text{0}}{\overset{\text{T}}{\int }}{\displaystyle \underset{\text{m}}{\int }\text{(}{\displaystyle \sum _{\text{α = 1}}^{\text{N}}{\stackrel{\mathrm{..}}{\text{q}}}_{\text{α}}}}}{\overrightarrow{\text{W}}}_{\text{α}}{\text{)}}^{\text{2}}\text{dm dt}$$

In the assumption of mutual orthogonality ${\overrightarrow{W}}_{\alpha }$ and ${\overrightarrow{W}}_{\beta }$ at $\alpha \ne \beta$ :

$$J=\frac{1}{2}{\displaystyle \underset{0}{\overset{T}{\int }}{\displaystyle \sum _{\alpha =1}^N{\left({\ddot{q}}_{\alpha }\right)}^2}{\displaystyle \underset{m}{\int }{W}_{\alpha }{}^{2}dmdt}=\frac{1}{2}{\displaystyle \underset{0}{\overset{T}{\int }}{\displaystyle \sum _{\alpha =1}^N{\left({\ddot{q}}_{\alpha }\right)}^2}}{W}_{\alpha \alpha }dt}\text{ (4)}$$

Here $W_{\alpha \alpha }\text{ = }{\displaystyle \underset{m}{\int }{W}_{\alpha }^{2}dm}$ For bending oscillations of homogeneous beams, $W_{\alpha \alpha }\equiv m$, where m is mass of one flexible element. As a result, $W_{\alpha \alpha }$ in (4) can be omitted.

We present the equations of motion (3), which take into account (2), as the constraints that are imposed on the phase variables $q_{\alpha }$, as follows:

$${\ddot{q}}_{\alpha }+2n_{\alpha }{\dot{q}}_{\alpha }+\left[{\Omega }^2-{\dot{\psi }}^2\left({\gamma }_{12}^2+{\gamma }_{13}^2\right)\right]q_{\alpha }\text{ = }{R}_{\alpha }\left[\ddot{\psi }{\gamma }_{12}+{\dot{\psi }}^2{\gamma }_{11}{\gamma }_3\right]\text{ (5)}$$

Practice shows that taking into account of structural damping in problems of control of SC reorientation has no essential meaning as a number of the periods of oscillations under the lowest modes considered in the mathematical model of a large flexible SC, during maneuver does not exceed 1-3. Therefore, with a good accuracy it is possible to suppose ${\text{n}}_{\text{α}}\text{ = 0}$.

Choosing as a control $u=\ddot{\psi }$, we came to the integral constraint ${\displaystyle \underset{0}{\overset{T}{\int }}{\displaystyle \underset{0}{\overset{t}{\int }}u\left(\tau \right)}}d\tau dt=\Psi$.

Let us introduce new variables

$z_1={\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{\tau }{\int }}u\left(t\right)}}dtd\tau$, $a_k\text{ = }{R}_k{\gamma }_{12}$  ${\text{z}}_{\text{2}}\text{ = }{\displaystyle \underset{0}{\overset{t}{\int }}u\left(\text{τ}\right)}\text{dτ}$, $z_{2k+1}=q_k$, $z_{2k+2}\text{ = }{\dot{q}}_k$ and notations $a_k\text{ = }{R}_k{\gamma }_{12}$, $b={\gamma }_{12}^2+{\gamma }_{13}^2$. For a case of a slewing of the SC "from rest to rest" we come to the following variation problem with the fixed boundaries:

$${\dot{z}}_1=z_2,{\dot{z}}_2=u,{\dot{z}}_{2k+1}=z_{2k+2}$$,

$${\dot{z}}_{2k+2}=-{\Omega }_k^2{z}_{2k+1}+b{z}_2^2+d{z}_2^2{z}_{2k+1}+a_{k}u,\left(k=1,\mathrm{...},N\right)\text{ (6)}$$

$$J\text{ = }\frac{1}{2}{\displaystyle \underset{0}{\overset{T}{\int }}{\displaystyle \sum _{k\text{ = 1}}^N{\left(-{\Omega }_k^2{z}_{2k+1}+b{z}_2^2+d{z}_2^2{z}_{2k+1}+a_{k}u\right)}^2}}dt\text{ (7)}$$

$$z_i\left(0\right)=0,\left(i=1,\mathrm{...},2N+2\right),\left(T\right)=\Psi ,z_j\left(T\right)=0,\left(j=2,\dots ,2N+2\right)\text{ (8)}$$

It is Lagrange problem on conditional extremum of the functional with the constraints (2.3). In the general case, the solution of the problem can be obtained only using the numerical methods.

Let us mark here a special case which take place when ${\text{γ}}_{\text{12}}\text{ =}{\text{γ}}_{\text{13}}\text{= 0}$ or ${\text{γ}}_{\text{11}}\text{ =}{\text{γ}}_{\text{12}}\text{= 0}$. Euler's axis in such a case coincides either with $O{x}_1$ or with $O{x}_3$. The equation (5) becomes homogeneous (control disappears) and the problem in the specified setting loses meaning.

Let us consider further ${\gamma }_{11}\ne 1$.

Questions of controllability and observability of considered object are in details researched earlier [13].

The Program of the Optimal Slewing

Using the Principle of maximum, we reduce the problem of the optimal control to the two-point boundary problem for a non-linear system of $\text{2M = 4}\left(\text{N + 1}\right)$ ordinary differential equations (ODE) of the first order.

$$J\text{ = }\frac{1}{2}{\displaystyle \underset{0}{\overset{T}{\int }}{\displaystyle \sum _{k\text{ = 1}}^N{\left(-{\Omega }_k^2{z}_{2k+1}+b{z}_2^2+d{z}_2^2{z}_{2k+1}+a_{k}u\right)}^2}}dt\text{ (9)}$$

The boundary conditions of the problem are

$x_1\left(0\right)=\Psi ;x_i\left(0\right)=0\left(i=2,\mathrm{...},M\right)$   $x_j\left(T\right)=0\left(j=1,\mathrm{...},M\right)\text{ (10)}$

For solution of such a boundary problem it is expedient to use Newton's method (the method of quasilinearization).

We select the solution of the boundary problem obtained from (9) by rejection of non-linear terms as an initial approach x⁰(t). The linearized equations for all subsequent approximations can be obtained by a standard expansion of the right parts of the equations (10) into Taylor series in a neighborhood of the solution obtained from the previous approach, saving all linear terms. It is possible to present the recurrence relations for the appropriate equations as follows:

$${\dot{x}}_s^{\left(n\right)}={\phi }_s\left(x^{\left(n-1\right)}\right)+{\displaystyle \sum }_{P=1}^{2M}{g}_{sp}^{\left(n-1\right)}\left(x_p^{\left(n\right)}-x_p^{n-1}\right),\left(s=1,\mathrm{...},2M;p=1,\mathrm{...},2M\right);$$

$${\text{g}}_{\text{sp}}^{\left(n-1\right)}\text{ = }\partial {\text{φ}}_{\text{s}}\text{/}\partial {\text{x}}_{\text{p}}|{}_{{\text{x = x}}_{\text{S}}^{\left(n-1\right)}}\text{ (11)}$$

As a result, the system of the equations for all approximations, except initial, turns to inhomogeneous one with variable coefficients. The boundary conditions (10) are the same in all iterations.

From the ODE theory it is known that the general solution of the inhomogeneous ODE can be built as the sum of any partial solution of the inhomogeneous equation and the general solution of the appropriate homogeneous equation. The arbitrary partial solution of inhomogeneous ODE can be obtained from the Cauchy problem for this equation with the arbitrary initial conditions. It is possible to take them to be homogeneous.

Let

$$x_s\text{ = }{y}_s+z_s\left(s\text{ = 1,}\mathrm{....}\text{,2}M\right)\text{ (12)}$$

Here $z_s$ is the partial solution of the inhomogeneous Cauchy problem with homogeneous initial conditions:

$${\dot{z}}_s^{\left(n\right)}\text{ = }{\displaystyle \sum _{p\text{ = 1}}^{2M}{g}_{sp}^{\left(n-1\right)}}{z}_p^{\left(n\right)}+L_s\left(t\right),\left(s\text{ = 1,}\mathrm{....}\text{,2}M;p\text{ = 1,}\mathrm{...}\text{,}M\right)\text{ (13)}$$

With initial conditions:

$$z_i\left(0\right)\text{ = 0}\left(i\text{ = 1,}\mathrm{...}\text{,2}M\right)\text{ (14)}$$

Here y_s is the solution of the boundary problem for homogeneous system (the additional equation):

$${\dot{y}}_s^{\left(n\right)}-{\displaystyle \sum _{p\text{ = 1}}^{2M}{g}_{sp}^{\left(n-1\right)}}{y}_p^{\left(n\right)},\left(s\text{ = 1,}\mathrm{...}\text{,2}M,p\text{ = 1,}\mathrm{...}\text{,}M\right)\text{ (15)}$$

With original boundary conditions:

$${\text{1}}^{\left(n\right)}\left(0\right)\text{ = -}\psi \text{,}{y}_i^{\left(n\right)}\left(0\right)\text{ = 0, }\left(i\text{ = 2,}\mathrm{...}\text{,}M\right)\text{ (16)}$$

$$y_i^{\left(n\right)}\left(T\right)\text{ = }{x}_i^{\left(n\right)}\left(T\right)-z_i^{\left(n\right)}\left(T\right),\left(i\text{ = 1,}\mathrm{...}\text{,}M\right)\text{ (17)}$$

Such an algorithm provides fast convergence in a region far from a resonance $\left(T\gg 2\pi /{\omega }_1\right)$. If duration of the maneuver is close to the period of oscillations of the system on the lowest frequency, the algorithm needs to be improved.

For example, [14] suggests building the solution of the inhomogeneous linear two-point boundary problem in a following form (notations are changed):

$$x_s^{\left(n+1\right)}\text{ = }{x}_s^{\left(n\right)}+\delta x_s^{\left(n\right)},\left(s\text{ = 1,}\mathrm{....}\text{,2}M\right)\text{ (18)}$$

I.e. some perturbation $\delta x_s^{(n)}$ is added to $x_s^{(n)}$, obtained on the previous iteration from the following linear inhomogeneous boundary problem:

$\delta {\dot{x}}_s^{\left(n\right)}\text{ = }{\displaystyle \sum _{p\text{ = 1}}^M{g}_{sp}^{\left(n\right)}}\delta x_p^{\left(n\right)}-\epsilon \left({\dot{x}}_s^{\left(n\right)}-{\phi }_s\left(x_p^{\left(n\right)}\right)\right),\left(s\text{ = 1,}\mathrm{...}\text{,2}M;p\text{ = 1,}\mathrm{...}\text{,}M\right)\text{ (19)}$

$$\delta x_i^{\left(n\right)}\left(0\right)\text{ = -}\epsilon \left(x_i^{\left(n\right)}\left(0\right)-x_i\left(0\right)\right),\left(i\text{ = 1,}\mathrm{...}\text{,}M\right)\text{ (20)}$$

$$\text{δ}{x}_i^{\left(n\right)}\left(T\right)\text{ = -}\epsilon \left(x_i^{\left(n\right)}\left(T\right)-x_i\left(T\right)\right),\left(i\text{ = 1,}\mathrm{...}\text{,}M\right)\text{ (21)}$$

The sequence of steps is such:

• To find $x_s^{(0)}$ from the linear part of the problems ;

• To build the boundary problem for the inhomogeneous equation with respect to $\delta x_s^{(0)}$;

• To find $\delta x_s^{(0)}$ as sums ${\text{δx}}_{\text{s}}^{\text{(0)}}{\text{ = y}}_{\text{s}}^{\text{(0)}}{\text{ + z}}_{\text{s}}^{\text{(0)}}\text{ (s = 1,…,2M)}$, for which we solve BVP and Cauchy problem such as it was explained above ;

• To find $x_s^{\left(1\right)}\text{ = }{x}_s^{\left(0\right)}+\text{δ}{x}_s^{\left(0\right)}\left(s\text{ = 1,}\mathrm{....}\text{,2}M\right)$;

• Further iterative process is continued;

The parameter ε is introduced from the following reasons: If the changes $\delta x_s^{(n)}$ on each step of iterations are selected too large, iterative procedure cannot converge. Therefore it is expediently to reduce artificially the error of current iteration. In process of fulfillment of serial approximations, value ε should increase gradually, aspiring to unit.

To the solution of such a boundary problem it is possible to apply the same algorithm, as the linear inhomogeneous boundary problem described above.

In the problem under consideration there are six phase variables, if to take into account two first modes of flexible oscillations. They are determined in initial and in terminal points. Values of the costate variables on boundaries are unknown. The problem is linear, therefore the principle of superposition of solutions is valid. Knowing six values of terminal conditions of the phase variables during the terminal instant, we present them as functions of solutions of Cauchy problems with known initial conditions for phase variables and with unknown in advance initial conditions for the costate variables. We designate last variables as ${\text{α}}_{\text{i}}\text{,}\left(i\text{ = 1,}\mathrm{...}\text{,6}\right)$. Now we solve numerically following Cauchy problems for the considered linear equation:

• One problem with the given initial conditions for phase variables. In our case it is $x_i\left(0\right)\text{ = 0,}\left(i\text{ = 1,}\mathrm{...}\text{,M}\right)$;

• Six problems with serial unit values of the costate variables at the initial instant;

As a result, it is possible to consider known values of terminal conditions as superposition of the obtained solutions with unknown coefficients ${\text{α}}_{\text{i}}\text{,}\left(i\text{ = 1,}\mathrm{...}\text{,6}\right)$ for the solutions obtained with unit initial conditions for each of the costate variables, namely:

$$x_i\left(T\right)\text{ = }{x}_i^{\left(1\right)}\left(T\right)+{\alpha }_1{x}_i^{\left(2\right)}\left(T\right)+{\text{α}}_{\text{2}}{x}_i^{\left(3\right)}\left(T\right)+{\text{α}}_{\text{3}}{x}_i^{\left(4\right)}\left(T\right)+{\text{α}}_{\text{4}}{x}_i^{\left(5\right)}\left(T\right)+{\text{α}}_{\text{5}}{x}_i^{\left(6\right)}\left(T\right)+{\text{α}}_{\text{6}}{x}_i^{\left(7\right)}\left(T\right)\text{ (22)}$$

If to denote the column vector with elements $x_i\left(T\right)-x_i^{\left(1\right)}\left(T\right)$, $\left(i\text{ = 1,}\mathrm{...}\text{,6}\right)$ by X(T), the matrix with elements $x_i^{\left(j\right)},\left(i\text{ = 1,}\mathrm{...}\text{,6;}j\text{ = 2,}\mathrm{...}\text{,7}\right)$ by $\widehat{X}\left(T\right)$, and the column vector with element ${\text{α}}_{\text{i}}\text{,}\left(i\text{ = 1,}\mathrm{...}\text{,6}\right)$ by A, it is possible to calculate unknown initial conditions for the costate variables in a form $\text{A = }{\left(\hat{\text{X}}\left(T\right)\right)}^{-1}\text{X}\left(T\right)$

In such a way the linear boundary problem is reduced to a series of Cauchy problems, which allow transferring terminal boundary conditions to the initial instant.

Numerical Example

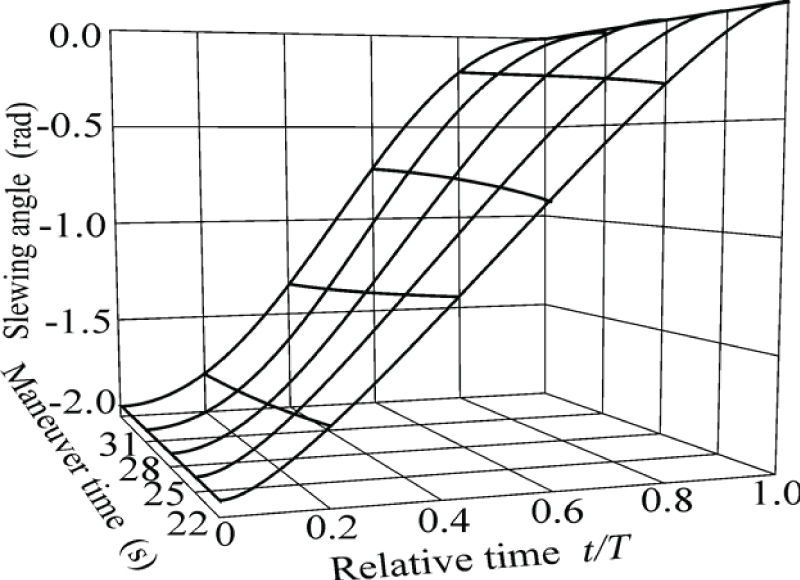
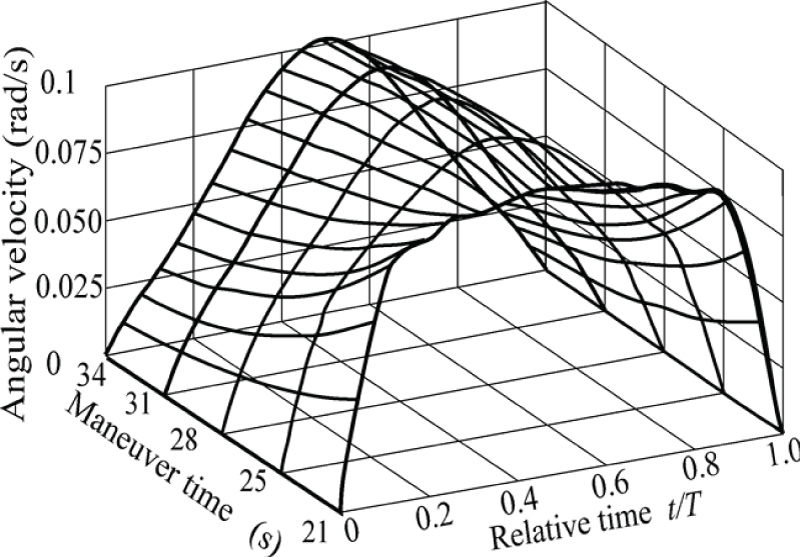
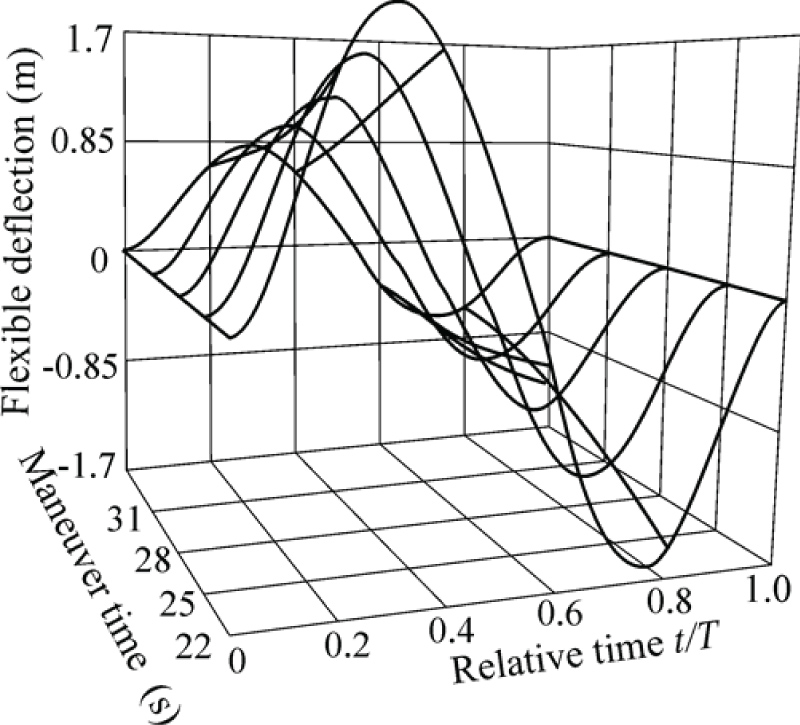
As an example we consider SC with the values of parameters accepted in [2]: Length of panels L = 30 m, linear density of panels μ = 0.2 kg/m, distance to edge of the panels r = 1 m, bending stiffness EJ = 1500 N/m², nominal time of the slewing T = 25 s. It is a case, when duration of the slewing is close to the period of system oscillations on the lowest frequency. For the solution of the non-linear boundary problem the great number of iterations and the special receptions providing convergence of iterative process in this case is required. 20 iterations were needed for creation of the program of the SC slewing corresponding to three serial rotations on angles of the order ${\phi }_i=1,2$ rad at T = 25 s. For T = 22 s, good accuracy of fulfillment of terminal boundary conditions (the order 1. Е-10 for all variables) and functional stationarity (difference of its values on adjacent iterations of the same order) have been reached only after 30 iterations. At a smaller T values, computing process diverges. For Т = 21 s, it was not possible to construct converging computing process.

Results of creation of the program of the slewing for various times of its duration ( $T\in [22,34]$ s) are shown in Figures 2, Figure 3, Figure 4 and Figure 5. From Figures it is visible that in the process of approach of duration values of the slewing to value of the period of oscillations on the first frequency, complexity of program control increases.

Behavior in time of angular velocity of the main body becomes complicated accordingly and deflections of the ends of panels of solar batteries increase (at Т = 22 s the maximum deflection reaches 1.7 m).

The solving of the considered non-linear boundary problem in each specific case can demand the big resources of the on-board computer. Besides, creation of the program of control admits certain errors since the real control of a slewing will provide the mandatory stabilizing torques. In this connection, creation of the program of the slewing using more simple algorithms based on the theory of approximation of vectorial fields or as it is accepted to speak in the literature, on the basis of technology of neural networks is admissible.

At creation of laws of control by maneuvers of the large flexible space structures developers often face necessity of carrying out of bulky and durable calculations on on-board computers. In this connection there is a necessity for creation of the controllers, allowing to minimize expenses of machine time and to be restricted by probably simpler on-board computer.

The last years, algorithms of creation of neural networks are developed for creation of control laws for a row of the characteristic modes of space systems. As the first, it is possible to specify creation of the program law of control by an optimal slewing on the arbitrary angle of the large flexible spacecraft such as a telecommunication spacecraft with objective to make maneuver without excitation of undesirable flexible oscillations of a construction after its end. Development of the neural network is supposed also, allowing accumulating the information for creation of control by a liquidation of the mode of librational (pendulum) oscillations in a plane of an orbit of a large flexible space tether. During deployment in an orbit, the tether is led in the end of deployment to a local vertical without excitation of longitudinal oscillations of its cable. The similar problem can be formulated for process of deployment of a flexible tether of two bodies with delivery one of bodies in the prescribed neighborhood of an object of a space debris, which must be removed from an orbit.

Creation and Training of the Neural Network

For implementation of such an approach it is expediently usage of neural networks, successfully developed at the last years. Such networks allow us to accumulate the information in their nodes during the preflight period, using powerful terrestrial computers (training of neural networks) and with split-hair accuracy to recover control laws in an orbit for current terminal conditions. Approximation of the vectorial fields defining laws of control based on the method of neural networks, demands essentially smaller amount of mathematical operations and can be fulfilled on more simple on-board computers.

Creation of the controller of direct communication (program or feedforward control) for the big angular maneuver of reorientation of the spacecraft with flexible panels, such as the telecommunication spacecraft is represented expedient. The controller is capable to calculate quickly the optimal input shape of the program control for a non-linear flexible system. It is reached by approximation of the dependences of the program control on the maneuver parameters in a network of radial basis functions (RBF). There is an algorithm of process of approximation of network RBF. The controller provides compensating of residual flexible oscillations for non-linear system and computing simplicity.

Such an approach assumes, first of all, parameterization of the required program of motion on the basis as a rule of spline approximation of any order, normally from 0 to 3 orders. Having set the enough dense network of nodal points in the space of parameters of a slew (in our case possible values in practice of the of serial rotations are ${\phi }_i,\left(i=1,2,3\right)$, it is possible in advance, during preflight preparation to solve the necessary amount of boundary problems, to parameterize each of the obtained solutions and to construct a vectorial field of these parameters over a space of possible values of slew parameters [2].

Handling or training of a neural network is produced in advance. In flight, it is necessary to recover values of parameters of control for the next point of space of parameters of a slew, as a rule, not coinciding with nodal points. The task is reduced to the solution of a system of the linear algebraic equations whose order is equal to number of nodes of the neural network. For recovery of the necessary information, various types of radial basis functions are used. Much attention to this direction of researches is given in [12].

Some authors tried to use neural networks for control of flexible systems. However, many of the offered network architecture use only a referential path, speed, and acceleration as inputs and, thus, can approximate and compensate only dynamics of a rigid part of system, for example, see [8]. To compensate dynamics of flexible elements, the neural network should have much more inputs corresponding to the state variables of the flexible system. It is difficult generally for carrying out, as complexity of a neural network normally quickly grows with dimensionality of its input.

Operation with the full control of a flexible system on the basis of the neural network, nevertheless, is fulfilled by [5]. They successfully controlled the experimental flexible pointing device at usage of the partial information on the dynamics of a system. Here we also result a case of control of flexible system, but suppression of flexible oscillations defines the selected objective function of the control.

In control of a maneuver of flexible system from rest to rest, using described approach, parameters of the task which are an input to a neural network, are defined by initial and desirable finite position of the main module of the system. Therefore at this approach, smaller complexity of the performance, the raised speed of convergence, accuracy, and simplicity of performance in comparison with approach of a neural network for problems of the inverse dynamics.

Further we consider algorithm of creation and training of a neural network with the subsequent recovery of values of the required program of a slew on the basis of a simple algorithm. For simplicity we will consider a case when the Euler slewing of the flexible spacecraft can be constructed as a result of its rotation around two axes on angles $\psi$ and $\vartheta$. Values of angles are not restricted. Setting and solving numerically the optimal control problem, we obtain the numerically the program control law u(t). Let us break a control time interval into 25 subintervals.

We select values of angles $\psi$ and $\vartheta$ that are equivalent to an Eulerian slew as parameters of control p for a mode of SC slewing from rest to rest. Let they have values in area $\psi \in \left[-1.05,\text{ 1}\text{.05}\right]$, $\vartheta \in \left[-1.05,1.05\right]$ with a step 0.3 rad. As a result we obtain 64 of pairs values of angles $\psi$ and $\vartheta$. To each pair we deliver in correspondence a network node. Passing to correspondent values of the angle of Eulerian finite rotation, we will have 64 feedforward control laws.

For each node, we solve the initial boundary problem of optimal control. Each obtained law of the control we approximate by cubic splines on 25 intervals and we save this information in the memory. This process is training of a neural network.

The problem is to find for each point in the parameter space feedforward control $\hat{\text{U}}\text{ = }\hat{\text{f}}\left(p\right)$ and to approximate it using the technology of the neural networks. The approximation parameters can be found off-line and the optimal feed-forward control can be found then using an on-board computer [12].

For approximation of the mapping $\hat{\text{U}}\text{ = }\hat{\text{f}}\left(p\right)$, RBF interpolation is used. It has the form:

$$\hat{\text{U}}\text{ = }\hat{\text{f}}\left(p\right)\text{ = }{\displaystyle \sum _{\text{j = 1}}^{{\text{N}}_{\text{a}}}{\text{V}}^{\left(j\right)}\text{h}\left({\text{p - p}}_{\text{j}}\right)}\text{ (23)}$$

For obtaining this mapping according to [13] as radial basis functions it is possible to use values $\text{h}\left(p\right)\text{ = }{\left(1+{\Vert p\Vert }^2/d^2\right)}^{-1/2}$ (Reverse Hardy Multiquadrics), where p is the vector of parameters of the slew, $\Vert \cdot \Vert$ designates Euclidean norm of a vector, d is the parameter of width of the radial function, which normally to select of the order of average distance between adjacent nodes of the network.

Thus, in the calculation program it is necessary to calculate the matrix elements H(16,16)

$$H\left(i,j\right)\text{ = h}\left(p_i-p_j\right)\text{ = }{\left(1+{\left(p_{i1}-p_{j1}\right)}^2+\left({\left(p{i}_2-p_{j2}\right)}^2\right)/d^2\right)}^{-1/2}\text{ (24)}$$

Calculating for each node of a network control in the form of a Table 1 valued function u (0:25) (at the integration step h = 0.01 s it is saved each 100-th point), we obtain the matrix $\Vert U^{\left(1\right)},\mathrm{...},U^{\left(64\right)}\Vert$ 64 × 26, composed of input vectors for each a node. Further, it is necessary to construct a matrix consisting of weight vectors V (64) of type:

$\text{VV}\left(i,j\right)\text{ = }\left[V^{\left(1\right)},\mathrm{...},V^{\left(64\right)}\right]{\text{ = H}}^{\text{ - 1}}\left[U^{\left(1\right)},\mathrm{...},U^{\left(64\right)}\right]\text{, }\left(i\text{ = 1,}\mathrm{...}\text{,26; j = 1,}\mathrm{...}\text{,64}\right)\text{ (25)}$

Now, selecting values of parameters of a slew, namely, ${\text{φ}}_{\text{1}}\text{ = 0}\text{.3}$, ${\text{φ}}_{\text{2}}\text{ = 0}\text{.3}$, which do not coincide with network nodes, we calculate a control vector for such a slewing using the neural network:

$$\hat{\text{U}}\text{ = }\hat{\text{f}}\left(p\right)\text{ = }{\displaystyle \sum _{\text{j = 1}}^{{\text{N}}_{\text{a}}}{\text{V}}^{\left(j\right)}\text{h}\left({\text{p - p}}_{\text{j}}\right)}\text{ (26)}$$

Parallel, for this point, the boundary problem has been solved, and spline approximation of the obtained solution is passed. Further comparative numerical simulation of the slew of the flexible SC for these three cases of creation of controlling function has been led. As a result, following values of phase variables at the instant of the rotation termination have been obtained:

In case of need to obtain more accurate satisfaction of the terminal boundary conditions, it is necessary to specify on the one hand the parametric representation of solutions of the boundary problem, and with another - to reduce the distances between nodes of the neural network.

Conclusion

This paper describes the problem of construction in orbit of the optimal feedforward control law for slewing of the spacecraft with attached flexible appendages in the class of slewing around the Eulerian axis. The problem of optimal reorientation of spacecraft with nontraditional objective of control, reducing to a minimum the dynamic overload of flexible elements in a relative motion is formulated. Use of the obtained control law allows one to make the behavior of elastic appendages as close as possible to the quasi-static motion during the slewing maneuver. For on-ground calculation, the numerical solution is obtained using the developed effective algorithm for solving the non-linear boundary-value problem. The solution of a problem of the optimal control in an orbit demands sometimes enough durable calculations even on the modern computers. Approximation of the vectorial fields determining program (feedforward) laws of control based on a method of neural networks demands essentially less of mathematical operations and can be realized on more simple on-board computers. The network whose training can be made during of preflight preparation is created in space of the slewing parameters. Simulation of fast calculations of the parameters of the optimal slewing program in flight is made on the basis of use of known radial basic functions. Comparison of accuracy of boundary condition satisfaction for considered methods of feedforward control building is shown at the end.

---