International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 4, Issue 1
Research Article
DOI: 10.35840/2631-5068/6512
Power-Invariant Magnetic System Modeling
Guadalupe G González1* and Mehrdad Ehsani
Table of Content
Figures
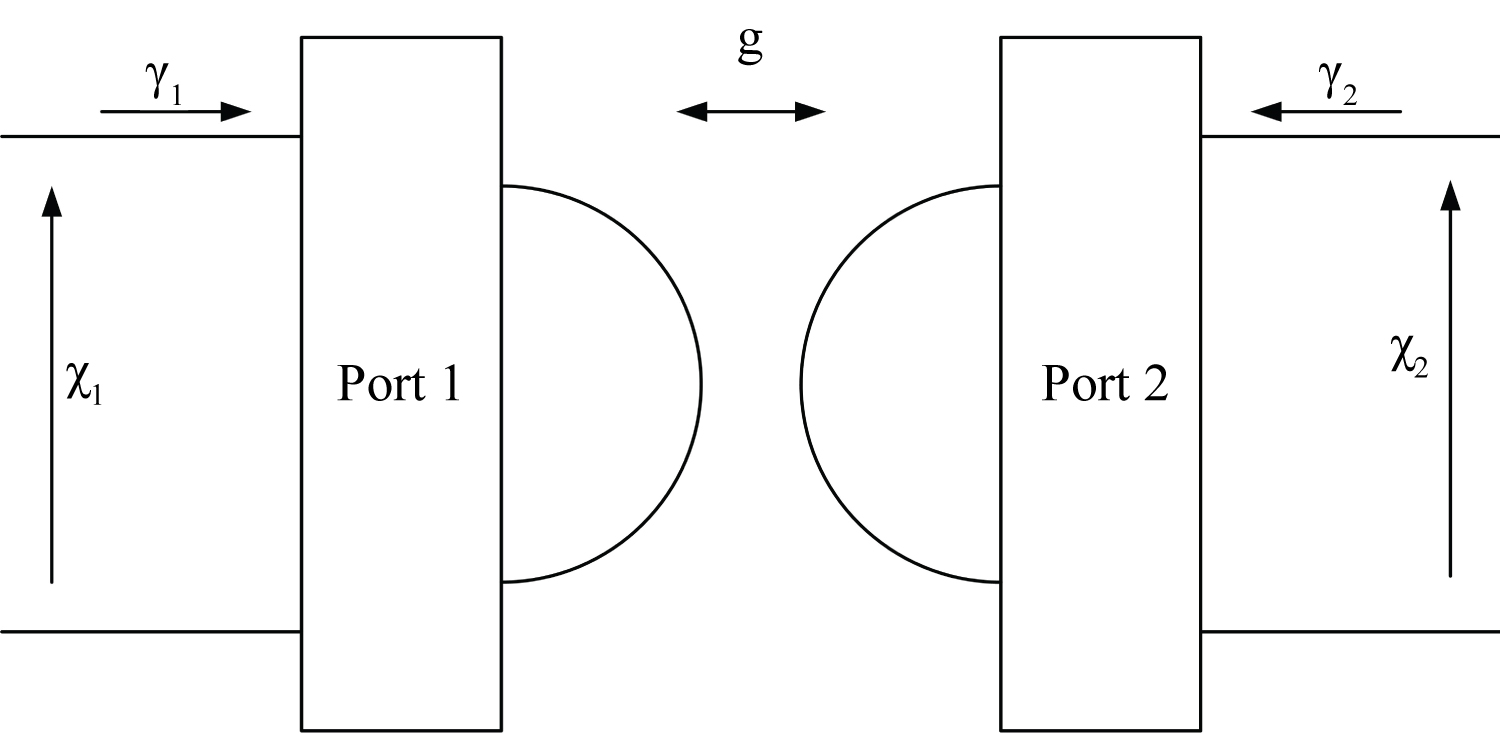
Figure 1: Symbolic representation of a two-port gyrator...
Symbolic representation of a two-port gyrator.
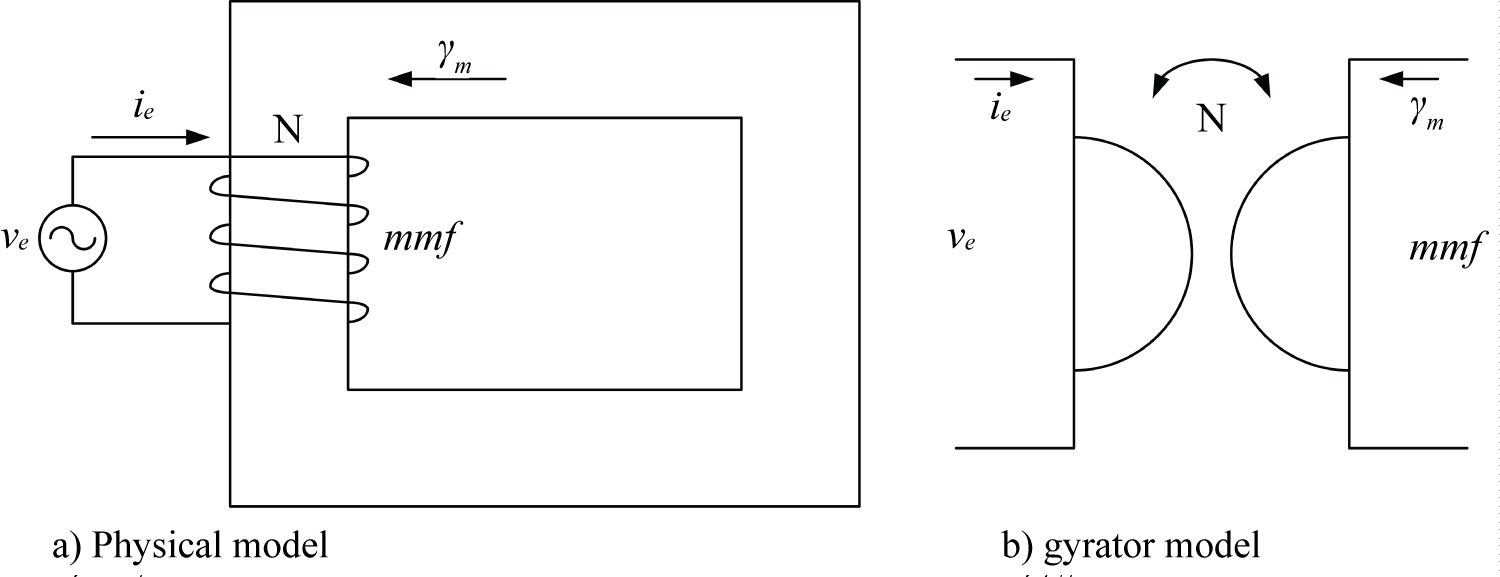
Figure 2: Representation of an iron core coil as a) Physical; b) Gyrator models...
Representation of an iron core coil as a) Physical; b) Gyrator models.
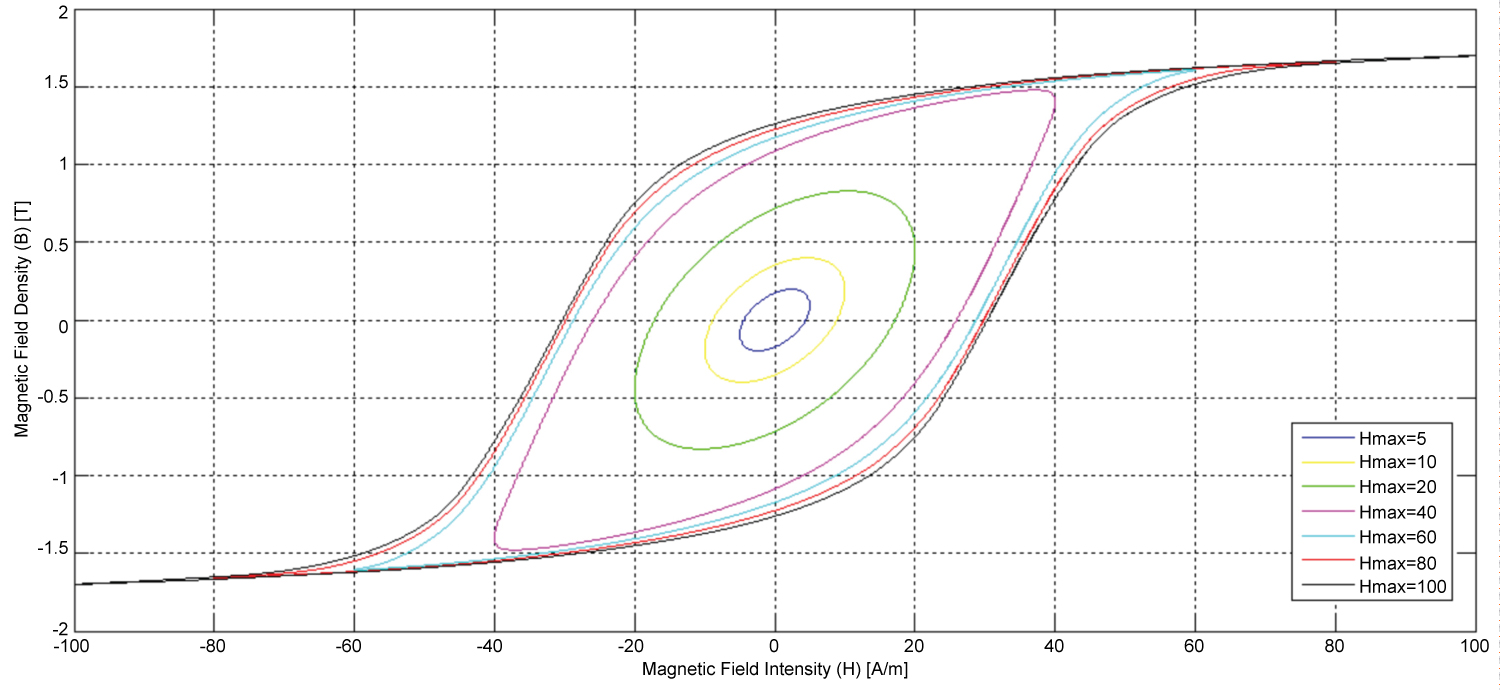
Figure 4: Family of hysteresis loops at different amplitudes at 60 Hz...
Family of hysteresis loops at different amplitudes at 60 Hz.
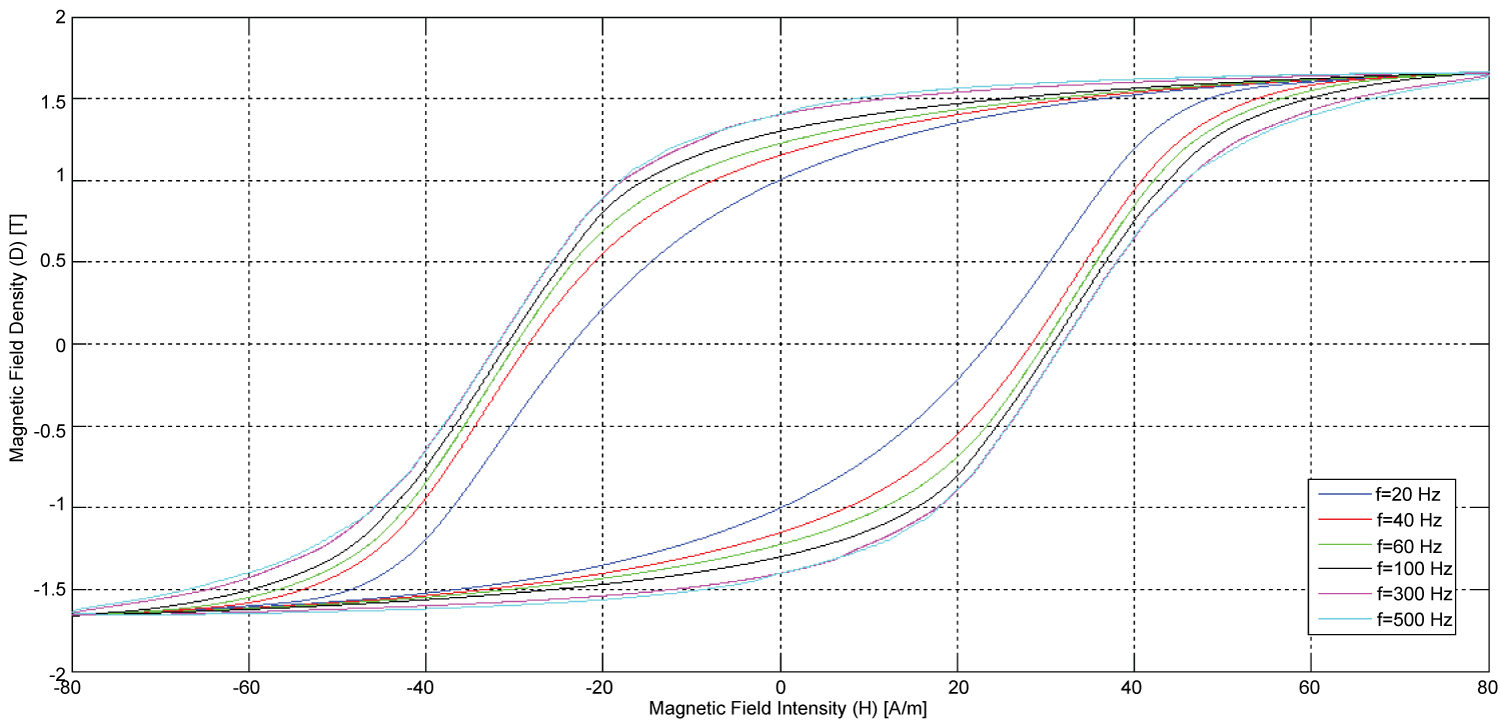
Figure 5: Family of hysteresis loops at different frequencies...
Family of hysteresis loops at different frequencies.
Tables
Table 1: Calculation of power in different media.
Table 2: Different media analogs.
Table 3: Comparison of the Power-Invariant and reluctance models.
References
- RW Buntenbach (1969) Analogs between magnetic and electrical circuits. Electronic Products 12: 108-113.
- VP Popov (1845) The principles of theory of circuits. Higher School, Russia, Moscow, 496.
- DC Hamill (1994) Gyrator-capacitor modeling: A better way of understanding magnetic components. In: Proc 9th Annu Applied Power Electronics and Conference and Exposition, Orlando, Florida, 1: 326-332.
- DC Hamill (1993) Lumped equivalent circuits of magnetic components: The gyrator-capacitor approach. IEEE
- RY Barazarte, GG González, M Ehsani (2010) Generalized gyrator theory. IEEE Trans Power Electron 25: 1832-1837.
- SS Attwood (1956) Electric and magnetic fields. In: Electric current. (3rd edn), John Wiley & Sons, New York, 116-118.
- GG González (2011) Power-invariant magnetic system modeling. Ph.D. dissertation, Texas A&M University, College Station, TX.
Author Details
Guadalupe G González1* and Mehrdad Ehsani
Department of Electrical and Computer Engineering, Texas A&M University, USA
Corresponding author
Guadalupe G González, Department of Electrical and Computer Engineering, Texas A&M University, College Station, TX 77840, USA.
Accepted: March 10, 2018 | Published Online: March 12, 2018
Citation: González GG, Ehsani M (2018) Power-Invariant Magnetic System Modeling. Int J Magnetics Electromagnetism 4:012.
Copyright: © 2018 González GG, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper, we present an alternative to modeling magnetic systems using a more consistent approach to lumped parameters. The model we introduce is consistent with other energy system models and allows the engineer to draw analogies from other energy systems to gather insights and a clearer understanding of magnetic systems which up to now has not been available. First, the justification for our new approach and a literature review of other models based on lumped parameters is presented in order to highlight the differences between those and our model. Then, the fundamentals of electromagnetism and magnetic materials that are the underpinnings of the proposed magnetic model are presented. Finally, theoretical verifications are performed in a case study system for magnetic network identification to validate our model.
Keywords
Electromagnetic modeling, Magnetic analysis, Magnetic circuits, Magnetic hysteresis, Magnetic losses
Introduction
In all energy systems the parameters necessary to transmit power are similar in functionality, an effort or force (χ) is needed to create a flow in a medium and a flow or rate of change results (γ). Consequently, the power equation can be generalized as,
The previous statement can be supported by analyzing Table 1 where the generalized power equation holds true in at least three media, electrical, mechanical and hydraulic. However, this general power relationship does not hold true in the reluctance model, which is the conventional model of magnetics systems. Furthermore, by studying the electrical and mechanical models we realize that there are six recurrent quantities that describe the macroscopic behavior of any of these media (see Table 2). We generalized these quantities as the conserved quantity, flow, effort and three passive elements that establish the amount of energy that is either stored in a media or dissipated as heat.
It is noted that the conventional magnetic model does not follow the same pattern as the other media. First, the generalized power equation is not satisfied, second, three of the six quantities that standardize the models have not being defined and finally, there is a well-known reluctance/resistance analogy misconception [1].
Based on conservation of energy and related principles, we assumed that all media follow a similar power transmission pattern. Therefore, the inconsistency seen in the power equation at the magnetic regime suggests that modifications could be made to be consistent with the other energy regime models.
In this paper, we present a consistent model for magnetic media using lumped parameters. First, we will present a literature review of the three magnetic models based on lumped parameters in order to establish the differences between these models and the one we are proposing, which we called the power-invariant magnetic model. Then, we will introduce the fundamental justification of our model based on electromagnetism and magnetic materials. Finally, we will conceptually illustrate our theory by modeling a simple but relevant magnetic system: an iron core coil.
Literature Review
Several lumped parameter models have been developed for magnetic systems. The reluctance model is the oldest and most widely used in magnetic analysis therefore we consider it as the conventional magnetic model. In this section, we present a brief description of the reluctance model as well as other lumped parameter models that have been developed in order to provide a solution to the deficiencies of the reluctance model.
The reluctance model
This model is based on Hopkinson's law, which is analogous to Ohm's law for electric circuits.
In electrical circuits, Ohm's law is an empirical relation between the electromotive force (emf), potential (U) or voltage (ve) needed in order to produce a flow of current (I) through a conductor. It can be expressed as,
Where R is the resistance [Ω].
In magnetic circuits, Hopkinson's law is an empirical relation betweesn the magnetomotive force (mmf) and the magnetic flux (φ) given by,
Where is the reluctance [H-1].
When the reluctance model was defined, it was considered equivalent to the electric model in both form and functionality, but through the years it has been well established that this is not the case. The main difference between these expressions is that in electrical circuits, the resistance is a measure of how much energy can be dissipated as heat while current flows in the material. However, in magnetic circuits the reluctance is a measure of magnetic energy storage rather than a measure of magnetic energy dissipation. In other words, magnetic losses (Pm) cannot be calculated using an analogue of Joules law as done for electric losses (Pe) in the electric regime. That is,
One of the reasons why the reluctance model has been successfully used for so long is that it is a quasi-static model. At low frequencies, the magnetic material shows almost zero heat losses and the reluctance model represents quite accurately the material's behavior under this condition. However, when alternating currents at medium or high frequency excite the magnetic material, heat losses are more relevant and the reluctance model becomes inconsistent. Consequently, other methods are applied in order to calculate the magnetic losses. For instance, hysteresis losses which are heat losses resulting from the tendency of the material to oppose a change in magnetism can be calculated using the area of the hysteresis loops. These hysteresis power losses (Ph) are given by,
Where V is the volume of the specimen [m3], f is the frequency of operation [Hz] and Aloop is the area of the hysteresis loop.
The permeance-capacitor model
In 1969, R.W. Buntenbach from the University of California stated that there are several stumbling blocks that inhibit the progress of magnetic circuit theory [1].
In an effort to correct the conventional model, Buntenbach proposed a different one also based on an analogy between electrical and magnetic quantities. In his model, the flux is analogous to electric charge, contrary to the reluctance model where flux was analogous to electric current. Also, the terms flux rate, magnetic resistance, magnetic inductance and magnetic impedance were introduced. However, the main contribution of this model is that it presents the Permeance-Capacitor analogy.
Buntenbach's model suggests that the magnetic circuit is better represented as an analogue to an electric capacitance rather than an electric resistance, which is true in functionality and can be validated by examining energy relations.
Assuming energy in the magnetic regime (Em) is calculated as the energy an electric capacitor (Ee) the dimensions are consistent,
Where C represents the electric capacitance [F], V the electric voltage [V], the permeance [H] which is and mmf is the magnetomotive force [t•A].
The gyrator-capacitor model
In 1993, Dr. Hamill applied gyrator theory in order to redefine the quantities of the reluctance model. In the Gyrator-Capacitor model, the permeance is also used analogous to the electric capacitance, however, it is the only circuit quantity of the model, contrary to the Permeance-Capacitor model which includes expressions for magnetic resistance and inductance. However, in later publications appear extensions to the original gyrator-capacitor model where a magnetic resistance and magnetic inductance are defined but there is neither a comprehensive description nor an application of them [2].
Hamill applied the gyrator-capacitor approach to model: A gapped-core inductor, a two-winding transformer and a Ćuk converter in quasi-static conditions with satisfactory results [3,4].
Power-Invariant Magnetic Model
As mentioned earlier, in the conventional magnetic model the power equation is not satisfied. This means that either the effort or flow quantity is not properly defined. We will use gyrator theory in order to identify the ill-defined quantity and redefine it.
Gyrator theory
The gyrator is a power-invariant, multiport network that converts the effort (χ) or flow (γ) quantity of one of the networks into its dual with respect to its gyration constant (g) [5], this is
A symbolic representation of a conventional two-port gyrator is presented in Figure 1. It can be shown that an iron core coil is a gyrator where the primary network is the electric side and the secondary network is the magnetic side and the two networks are coupled through the gyrator constant which is the number of turns (N) as shown in Figure 2. We can identify the effort and flow quantities of each regime by comparing the gyrator equations (9, 10) with the system's performance equations, Faraday's and Ampere's laws, given by (11) and (12) respectively.
It is evident that these set of equations are similar in form and functionality. Equations (9) and (11) suggest that the electric voltage (ve) is the effort quantity of the electric network while the rate of change of flux (dφ/dt) is the flow quantity of the magnetic network. Similarly, (10) and (12) suggest that the magnetomotive force (mmf) and the electric current (ie) are the effort and flow quantities of the magnetic and electric regimes, respectively.
In order to verify that these quantities satisfy the power equation we perform a dimensional analysis in (13) and (14) obtaining watts units in both cases.
Using the rate of change of magnetic flux (dφ/dt) as flow is the fundamental modification to the magnetic model. It is the key to defining the rest of the parameters (magnetic resistance, inductance and capacitance) needed to standardize the magnetic model.
Magnetic fundamental quantities
In this section, we will define the six scalar quantities we consider standard to fully model energy transfer process specifically for the magnetic regime. We will use an electric analogy as the basis to derive the magnetic model because there is an intrinsic coupling between the two systems.
Conserved quantity
In the electric regime, the conserved quantity is the free charge (qe). Its iteration with an electromagnetic field or with other charged particles is the main cause of many electric phenomena. For instance, when charge carriers move in different media, such as metallic conductors and free space, an electric current is produced.
In dielectric materials, on the other hand, due to the tight atom-electron bonds there are no free charges. The electric phenomenon is the result of the interaction of electric fields and the polarization charges of the dielectric material. These charges, which are basically electric dipoles, are known as bound charges to distinguish them from the free charges.
The scalar quantity that represents the polarization of the bound charges (P) due to an electric field intensity (E) is the electric flux (ψ) and it is expressed as,
Where represents the permittivity of air.
According to Gauss's law, the free charge contained in a volume (V) is equivalent to the electric flux density (D) through a surface (S) which encloses a volume (V). Therefore, we will assume the electric flux as a representation of the conserved quantity in dielectric materials.
Fundamentally, the magnetic phenomenon is the result of the magnetization of the magnetic dipole moments, similar to the electric phenomenon being the result of the polarization of the electric-bound charges in dielectric materials. We will use this analogy to define the magnetic conserved quantity.
The scalar quantity that represents the magnetization (M) of the magnetic material due to a magnetic field intensity (H) is the magnetic flux (φ) and it is expressed as,
Where μ0 represents the permeability of air.
Similar to the electric flux, we will use the magnetic flux (φ), which is the magnetic flux density (B) through a surface (S), as the magnetic conserved quantity. In order to be consistent with the electric analogy, we will refer to the magnetic conserved quantity as the flux (φ) or as a magnetic- bound charge (qm).
Flow
The flow can be defined as the movement of a conserved quantity through certain cross-sectional area per unit of time. In the electric regime, the flow or currents are divided into two classes, conduction currents and displacement currents. Conduction currents result from the movement of free charged particles in a conductive medium . The motion of these particles generates heat and therefore, it is usually associated with energy losses.
Mathematically it is given by,
Displacement currents were introduced by James Clerk Maxwell in 1861 in order to satisfy Amp�re's circuital law which establishes that currents always flow in a closed path. It satisfies the current through capacitors as there are no free charges moving inside the dielectric medium. Mathematically it is given by
Where ψ is used to denominate the electric flux [C].
Displacement currents play little role in metallic conduction. In metals, they are dwarf into insignificance by the magnitude of the conductive current; but in insulators where the conduction currents are weak, the displacement current may well play a role even at low frequencies and most certainly when the frequencies are elevated [6].
In magnetic systems, we propose to define the magnetic current as a displacement current similar to a dielectric material. This is based in the fact that both materials need to be polarized in order to react. Furthermore, the expression of flow obtained from the iron core coil as a gyrator suggests that
Which is similar in form, functionality and origin to (18) as both are based on flux. In this case φ is used to specify the magnetic flux.
Similar to electric displacement currents, the magnetic displacement currents are not based on the movement of magnetic free charged particles as the existence of such charges have not been discovered. Instead, they are based in the rate of change of magnetic fields. However, the displacement currents can be recognized as a moving-charge current related to the movement of the magnetic dipoles during the magnetization of the magnetic material. It is given by (19) or in terms of its current density as,
Since , the magnetic displacement current can also be expressed in terms of the magnetization as,
Effort
In general terms, the effort can be defined as the force needed to generate a flow or as the force needed to produce work. In electrical systems, the effort quantity is most commonly known as voltage (V), electric potential (Ue) or electromotive force (emf). It is the force needed to move a charged particle from one point to another in the presence of an electric field. Mathematically it can be expressed as,
Where E is the electric field intensity and dl is a differential element of a path.
In magnetic systems, the effort quantity has been specified as the magnetic potential (Um) or magnetomotive force (mmf), analogous to the electromotive force. In this paper, we will also refer to it as magnetic voltage analogous to electric voltage. Mathematically it can be expressed as,
Where H is the magnetic field intensity and dl is a differential element of a closed path.
In order to satisfy the analogy, the mmf must also be defined as the force needed to generate a magnetic current. This statement contradicts the popular notion that there is no flow of anything in a magnetic circuit corresponding to the flow of charge in an electric circuit. However, we have already established that the magnetic current is a displacement current and can be considered as the result of magnetization of the magnetic dipoles in magnetic materials, similar to the displacement current related to the bound or polarized charge of an electric insulator. In both cases, an effort is needed to create the polarization of the bound charges.
Resistance
As a standard model element, resistance can be generalized as the parameter that causes energy to be released as heat due to the flow of current in a material. Its generalized definition in terms of flow (γ) and effort (χ) is as follows,
In electric circuits, the resistance relates the electric voltage (ve) and current (ie) flowing through a conductive material,
Also, its value can be expressed in terms of the intrinsic property of the material (resistivity, ρe [Ω•m] or conductivity, σe [Ω-1/m]) and the geometry (length, l [m] and area, S [m2]) of the specimen. This is given as
Similarly, in magnetic circuits we can define a magnetic equivalent resistance based on the general definition. It is the quantity that measures the amount of magnetic current the material allows to flow when certain voltage is applied. It also causes energy to be lost as heat.
We can relate the magnetic current (im) and the magnetic voltage (vm) using,
Or in terms of the intrinsic property of the magnetic material (magnetic resistivity, ρm [Ω-1•m] or magnetic conductivity, σm [Ω/m]) and the geometry (length, l [m] and area, S [m2]) of the specimen as,
It is important to point out that there is a fundamental difference between the electric and magnetic resistance and this has its origins in the mechanism that produces the flow of currents. The electric resistance describes the opposition that the conductive media presents to the flow of free charges. Therefore, it reflects the heat losses due to the kinetic energy released by the movement of these free charges. However, as we established earlier, the magnetic currents result from the polarization or magnetization of the magnetic dipoles in the magnetic material, similar to the displacement electric currents. The power dissipated as heat is the result of the resistance of the magnetic material to being magnetized.
The power dissipated by the magnetic resistance can also be expressed in terms of an analogy to the Joule's law when the resistance is a constant value. That is,
Which is the average of the instantaneous power [W].
If the resistance is nonlinear, the power dissipated by the resistance can be calculated directly by calculating the average of the instantaneous power,
Capacitance
The capacitance can be generalized as the parameter that determines the amount of energy stored in the medium due to an applied effort (χ) in that medium. Mathematically it is expressed as,
Where qrw stands for conserved quantity in the medium.
In the electrical regime, the capacitance measures the ability of the medium to hold a charge (qe) due to a given potential (ve). For example, in an air capacitor it describes the amount of energy stored in the electric field. Electrical capacitance is expressed as,
For a dielectric capacitor with its intrinsic dielectric property and the geometry, capacitance can be expressed as,
Where l [m] and S [m2] represent the depth and area of the dielectric, respectively and ε [F/m] represents the permittivity of the dielectric material, which determines the ability of a material to polarize in response to an electric field.
The energy stored by a capacitor can be expressed as
In magnetic media, the capacitance determines the ability of the media to store energy due to a given magnetic potential or effort (vCm). The amount of energy stored in the magnetic medium can be expressed as,
Similar to the resistance, the capacitance depends on a property of the material medium. Its numerical value depends on the intrinsic property of the magnetic material (permeability, μ [H/m]) and the geometry of the material (length, l [m] and area, S [m2]). This is expressed as,
At this point, it is evident that our magnetic capacitance plays the same role as the permeance in the conventional reluctance model. Therefore, we have verified that the permeance and its inverse, the reluctance, are in fact energy storage elements and not the perceived dissipative elements.
Energy stored by a capacitance can be generally expressed as
If the capacitance is a constant value, then the energy stored can be expressed using a more familiar expression,
Inductance
In order to explain the inductance as a generalized element we need to remember the first law of thermodynamics, energy is neither created nor destroyed only transformed. This is important because energy can either be kept in the same medium of work or transformed into another medium in order to be stored.
The most common example of this process occurs in the electric regime when energy is stored in the magnetic medium due to the flow of electric current. The element that describes this process is known as electric inductance (Le) and is expressed as,
Where is the magnetic flux and is the electric current. The number of turns (N) appears in (39) because a gyration from the magnetic to electric regime is taking place.
Equation (39) can also be expressed in terms of the intrinsic property of the magnetic material (permeability, μ [H/m]) and the geometry of the material (length, l [m] and area, S [m2]) as,
The energy stored by the inductance can be expressed as,
Similarly, in magnetic systems the inductance determines the amount of energy stored in a dual medium due to the flow of magnetic current (im). As the electric and magnetic regimes are coupled, we consider the electric medium as the dual of the magnetic regime; therefore, the magnetic inductance (Lm) can be expressed as,
The magnetic inductance can also be expressed in terms of the geometry of the material, length (l) and area (S), and its permittivity (ε) as,
The energy stored by a magnetic inductance (WLm) can be expressed either by,
Or in the case that the inductance is a constant value by,
Finally, the inductance can be generalized as the element that stores energy in a dual regime or medium due to a flow (γ) and it can be expressed as,
Where qrw stands for conserved quantity in the dual medium.
To summarize, Table 3 presents a comparison of the power-invariant magnetic parameters proposed in this paper and those presented in the conventional reluctance model. Due to its completeness, the power-invariant magnetic model will be helpful in more accurately modeling the magnetic phenomena.
Case Study: Iron Core Coil
To illustrate the elements described in the power-invariant magnetic model we will use an iron core coil for a case study (see Figure 2). We use this case for several reasons. First, it is a simple structure, second, we are familiar with its physical behavior, and third, we want to represent the magnetic medium using the known material characteristics (B-H Loops, permeability curves, etc.).
According to [7], in quasi-static conditions the magnetic material can be characterized as a magnetic capacitor, as suggested by Hamill's gyrator-capacitor modeling technique [4]. However, the capacitance element alone does not represent the real behavior of an iron core coil. Hysteresis and magnetic losses, among other factors, need to be taken into consideration when modeling the magnetic medium. According to our theory, in order to represent the real behavior of the magnetic material we should model the medium using the magnetic resistance, inductance and capacitance. We understand that the effect of some of those elements is more dominant than others in the model. However, for completeness we will represent the medium based on all the three elements.
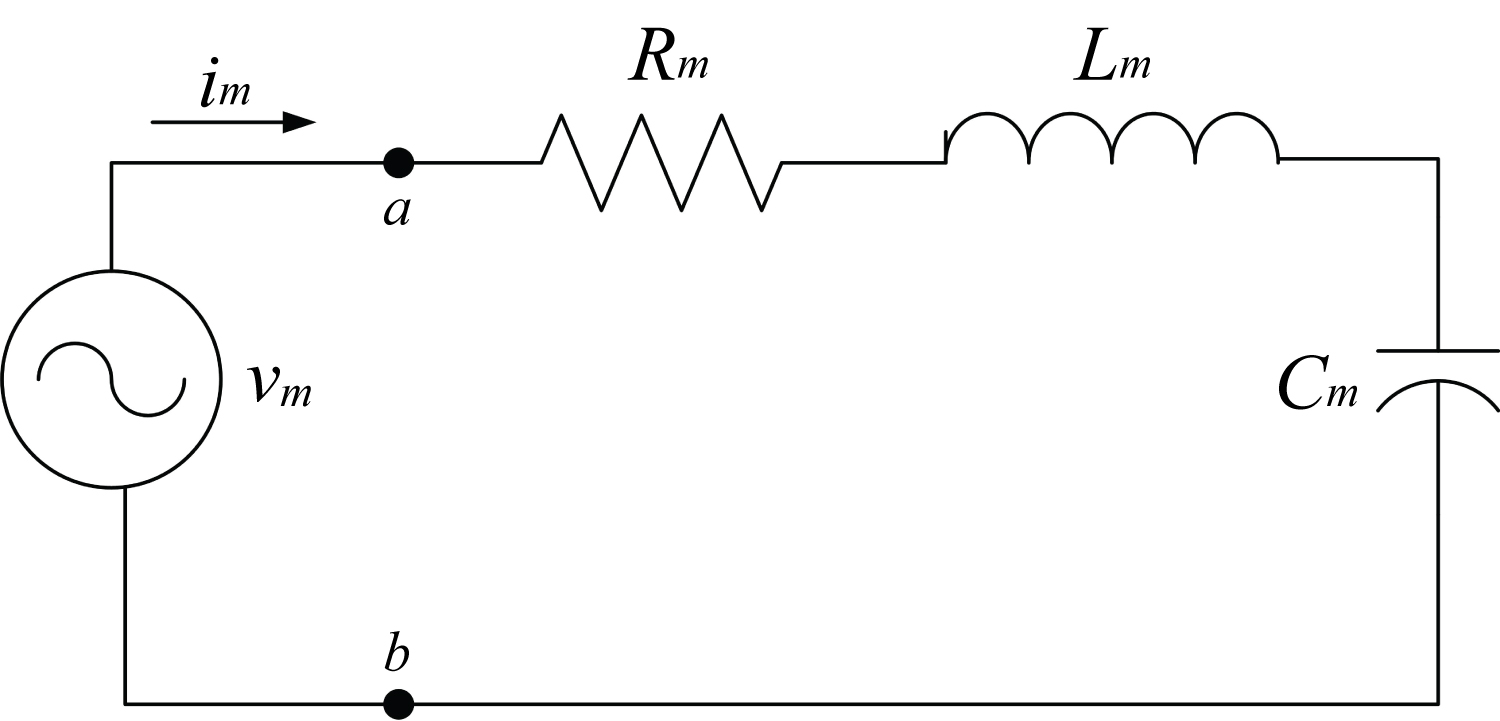
To develop an equivalent circuit model of the magnetic medium from scratch, there are eight possible configurations by which the magnetic elements could be arranged. However, after studying the system's response to different magnitude, frequency and waveform excitations, it is realized that there is only one configuration that satisfied the observed behavior of a magnetic material. Further, to produce the observed hysteresis behavior under ac excitation conditions, a nonlinear RLC series configuration is the suitable model (Figure 3).
The equation that represents this circuits is
Being the magnetic resistance, inductance and capacitance modeled as non-linear elements.
Figure 4 and Figure 5 show the B-H loops that result from modeling the magnetic medium as a nonlinear RLC series configuration, excited at different amplitudes and frequencies. It is important to point out that the study done in this section was based on a hypothetical magnetic material and a simulation experiment was done to validate that the general behavior of the magnetic iron-core model as we know it to the proposed power-invariant model. The magnetic voltage is related to the magnetic field intensity and the magnetic current is related to the magnetic flux density, both considering the geometry of the core.
Conclusion
In this paper, we have developed a unified magnetics model that is power-invariant under transformation of power from across electrical media. This model is consistent with other standard models used for other energy and power transfer media, such as electrical, mechanical, and hydraulic. This is useful for many reasons. First, following the principle of conservation of energy, all energy systems are expected to behave in a similar pattern during an energy transfer process (some energy is dissipated and some energy is reactively stored). Therefore, new insights and a different prospective can be attained for understanding magnetic system behavior by symmetry with other regimes. Second, the same analytical and numerical techniques can be applied across coupled power media in order to analytically compose and solve system differential equations. For instance, when working in the linear region of the characteristics of the magnetic material we could use phasors or Laplace transformations in order to solve the system's equations. This practice is not common in magnetic system analysis. Finally, we have now created a model where we are able to calculate power and energy for magnetic systems in a simpler and more traditional way, using the power equations.
The above theory can facilitate the development of better computer models of complex magnetic systems. It can also be instrumental in developing better design tools for magnetic devices and materials.
Acknowledgment
This work was partially supported by the government of the Republic of Panama through SENACyT-IFARHU's Professional Excellency Scholarship Program. Also, the generous gifts of the Industrial Affiliates of the Power Electronics and Motor Drives Laboratory at Texas A&M University are gratefully acknowledged.