International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 2, Issue 2
Research Article
DOI: 10.35840/2631-5009/7510
Studies on Two-Mode Spray Combustion
Lixing Zhou1* and Fang Wang2
Table of Content
- Abstract
- Keywords
- Nomenclature
- Greek Alphabets
- Subscripts
- Introduction
- A Simplified 1-D Model of Two-Mode Spray Combustion
- A Preliminary LES of Spray Combustion Accounting for Some Ignited Droplets
- A Droplet Ignition Model
- Results and Discussion
- The Suggested Model Equations of Two-Mode Spray Combustion
- The Suggested Solution
- Conclusions
- Acknowledgements
Figures
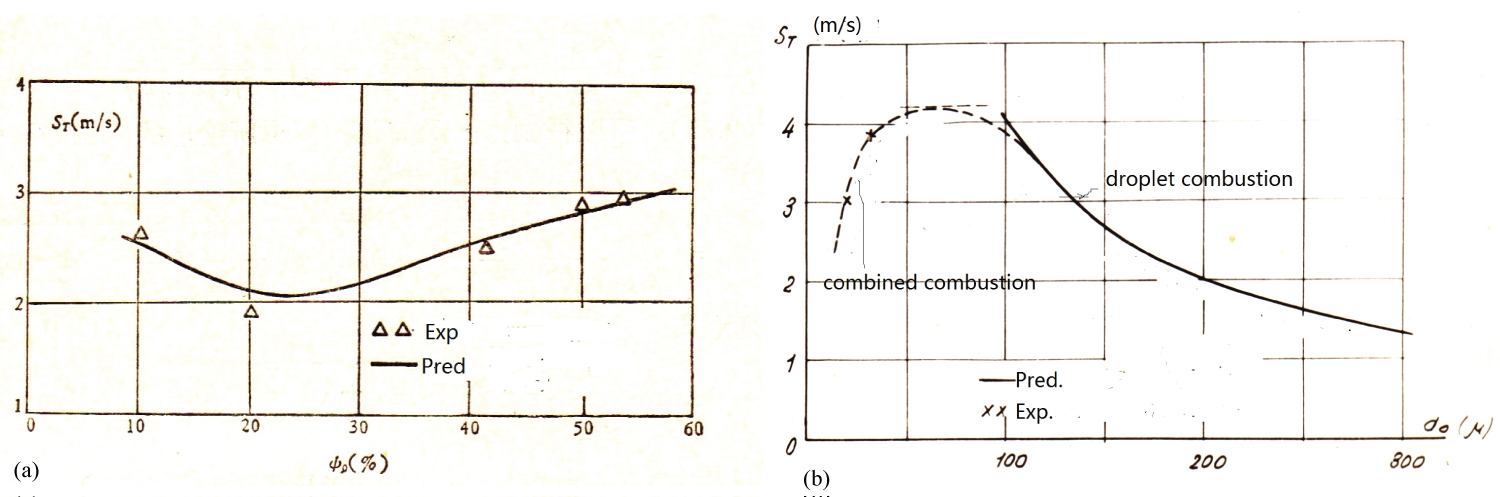
Figure 2: Spray flame propagation...
Spray flame propagation velocity. (Figure 2a vs. as pre-vaporization fraction; Figure 2b vs. as droplet size).
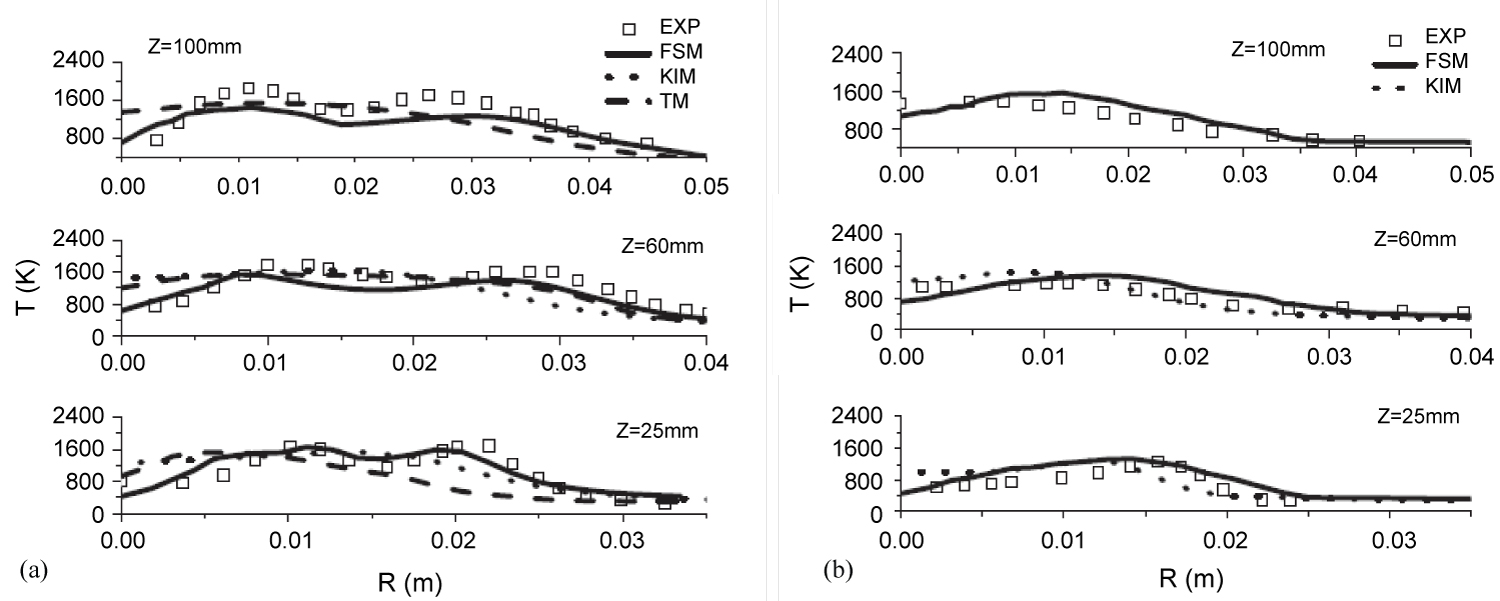
Figure 4: Temperature distribution for a...
Temperature distribution for a methanol-air spray flame. (Figure 2a-annular air flow rate 0 L/s; Figure 2b- 4.77 L/s).
References
- JH Burgoyne, L Cohen (1954) The effect of droplet size on flame propagation in liquid aerosols. Proceedings of Royal Society 225: 375-392.
- S Russo, A Gomez (2006) Physical characterization of laminar spray flames in the pressure range 0.1-0.9 MPa. Combustion and Flame 145: 339-356.
- LX Zhou, K Li (2015) Analytical and numerical studies on a single-droplet evaporation and combustion under forced convection. Acta Mechanica Sinica 31: 523-530.
- RJ Priem, MF Heidman (1959) Vaporization of propellants in rocket engines. ARS Journal 29: 836-842.
- YX Gu (1966) The effect of droplet size on the flame length and completeness of spray combustion. Science Bulletin 275-278.
- CC Miesse (1958) A theory of spray combustion. Industrial and Engineering Chemistry 50: 1303-1304.
- CK Law (1975) Asymptotic theory for ignition and extinction in droplet burning. Combustion and Flame 24: 89-98.
- CK Law (1978) Theory of thermal ignition in fuel droplet burning. Combustion and Flame 31: 285-296.
- SC Wong, XX Liao, JR Yang (1997) A simplified theory of the ignition of single droplets under forced convection. Combustion and Flame 110: 319-334.
- S Schnaubelt, O Moriue, T Coordes, C Eigenbrod, HJ Rath Zarm (2000) Detailed numerical simulations of the multistage self-ignition process of n-heptane isolated droplets with their verification by comparison with microgravity experiments. Proceedings of the Combustion Institute 28: 953-960.
- R Stauch, U Maas (2008) The ignition of methanol droplets in a laminar convective environment. Combustion and Flame 153: 45-57.
- Inkant Awasthi, Daniel N Popeb, George Gogos (2014) Effects of the ambient temperature and initial diameter in droplet combustion. Combustion and Flame 161: 1883-1899.
- SK Aggarwal (2014) Single droplet ignition: Theoretical analysis and experimental findings. Progress in Energy and Combustion Science 45: 79-107.
- DA Frank Kamenetsky (1955) Diffusion and Heat Exchange in Chemical Kinetics. Princeton University Press.
- EK Chekalin (1960) Spray Flame Propagation. Journal of Technical Physics 3.
- LX Zhou (1961) Evaporation and Combustion of Single-Droplets and Liquid Spray. Department of Physics and Mechanics, Leningrad Polytechnic University, Russia.
- LN Khitrin (1962) Physics of Combustion and Explosion. National Science Foundation.
- LA Kliachko, ZV Istratova (1960) On the theory of lower limits of flame propagation in two-phase mixtures. Proceedings of the Third All-Union Conference on Combustion Theory 2: 48-57.
- FA Agafonova, MA Gurevich, EF Tarasova (1960) Conditions for the stable combustion of single liquid-fuel droplets. Proceedings of the Third All-Union Conference on Combustion Theory 2: 29-39.
- F Wang, M Li (2016) The ignition of a mixed-fuel droplet in high-temperature stagnant air. The Chinese Symposium on Combustion.
Author Details
Lixing Zhou1* and Fang Wang2
1Department of Engineering Mechanics, Tsinghua University, Beijing, China
2School of Energy and Power Engineering, Beihang University, Beijing, China
Corresponding author
Lixing Zhou, Department of Engineering Mechanics, Tsinghua University, Tsinghua Garden, Haidian District, Beijing 100084, China, Tel: 86-10-62782231, E-mail: [email protected]
Accepted: August 22, 2017 | Published Online: August 25, 2017
Citation: Zhou L, Wang F (2017) Studies on Two-Mode Spray Combustion. Int J Astronaut Aeronautical Eng 2:010.
Copyright: © 2017 Zhou L, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Up to now the mechanism of spray combustion is considered as the un-ignited droplets evaporating in continuous gas flames, both in RANS modeling, LES and point-particle DNS. However, still in the 50's of the last century, experiments indicated that the spray combustion has different modes; it may be brush-like droplet diffusion flame-lets or cold droplets evaporating in blue gas flames. In this paper preliminary studies are made for two-mode spray combustion. At first a simplified analytical 1-D model for two-mode spray flame propagation is presented. The predictions are in agreement with the experimental results. The results indicate that different pre-vaporization fraction and different droplet sizes produce different flame modes. Secondly, a preliminary LES of spray combustion accounting for some ignited droplet is made with the assumption that some droplets will be ignited if their life time is greater than the ignition delay of a premixed gas-fuel-air mixture and the assumption of a same gas temperature for the evaporation of ignited and un-ignited droplets. The results show that the predictions accounting for the effect of ignited droplets is in better agreement with the experimental results, but the agreement is not always good due to lack of an appropriate droplet ignition model. In order to more accurately simulate the two-mode spray combustion, a simplified droplet ignition model is proposed using Frank-Kamenetsky's approximation for treating the highly nonlinear reaction term. The result gives the droplet ignition limits as a function of the gas relative velocity, droplet size and ambient gas temperature. To validate the proposed droplet ignition model, experimental studies on droplet ignition of a suspension droplet are carried out. The results show that the proposed model is in agreement with experiments. Finally, more accurate modeling equations of two-mode spray combustion are suggested for future RANS modeling, LES and point-particle DNS.
Keywords
Spray combustion, Combustion modes, Numerical modeling
Nomenclature
A: Empirical factor; B: Pre-exponential factor; cp: Specific heat; d: Diameter; D: Diffusivity; E: Activation energy; g: Gravitational acceleration; h: Enthalpy; k: Reaction-rate coefficient; m Mass; mass flow rate; : Evaporation rate; N: Total particle number flux; Particle number density; n: Particle number density; Nu: Nusselt number; p: Pressure; Pr: Prandtl number; Q: Heat; Heating effect; q: Heat of evaporation; S: Flame propagation velocity; source term; R: Universal gas constant; r: Radius; Radial coordinate; Re: Reynolds number; Sc: Schmidt number; Sh: Sherwood number; T: Temperature; t: Time; u,v,w: Velocity components; w: Reaction rate; x,y,z: Space coordinates; Y: Mass fraction
Greek Alphabets
α: Coefficient of excess air; β: Stoicheometric coefficient; δij: Kronic delta; µ: Dynamic viscosity; ν: Kinematic viscosity; λ: Heat conductivity; ρ: Density; τij: Shear stress; τrk: Particle relaxation time; e: Evaporation; F, fu: Fuel; f: Flame; g: Gas; i, j, k: Coordinate directions; components; ox: Oxygen; Oxides; p: Particle; r: Radiation; s: s species; sgs: Sub-grid scale; T: Turbulent; w: Wall; ∞: Oncoming flow
Subscripts
b: Boiling point; d: Droplet
Introduction
Turbulent spray combustion is a complex process. It includes droplet evaporation, gas-droplet turbulence fluctuations and their interaction, heat and mass transfer, gas chemical kinetics and turbulence-chemistry interaction in the gas phase. In most present simulations, including RANS modeling, LES and point-particle DNS, the mechanism of spray combustion is considered as un-ignited droplets evaporating in continuous gas flames. However, still in the 50's of the last century, it was found by high-speed photography that the spray flames have different modes. Burgoyne and Cohen [1] reported that for small-size droplets the flames look like blue transparent gas flames, but for lager-size droplets there are yellow brush-like flames. Recent high-speed photography [2] confirms these phenomena. These experimental results tell us that the spray flame may take different modes: unignited droplets evaporating in gas flames or a group of ignited droplets with diffusion flames, which is also in agreement with different combustion modes of a single droplet under different relative gas velocities [3], this is because the droplets of different sizes may be ignited (form enveloped flames) or un-ignited (form non-enveloped flames) under different gas temperatures, relative gas velocities. However, up to now in the simulation of spray combustion, including RANS modeling, LES and point-particle DNS, only the mode of unignited droplets evaporating in hot gas flames is taken into account. Hence the present simulation of spray combustion could not give the real physics of spray flames. Of course, the real pictures can be given by the fully-resolved DNS, but the problem of treating the interface with fast evaporation and the huge computation requirement remain to be solved. A more practical way is to simulate the multi-mode spray combustion in the scope of point-particle approach. In most practical cases there are droplet with different sizes, different gas relative velocities and under different gas temperatures, some of droplets may be ignited and others of them may not be ignited. The judgment should be the droplet ignition condition. The spray combustion includes at least two modes: ignited-droplet diffusion flames and un-ignited droplets evaporating in the gas flame.
In the 50's to 60's of the last century, some 1-D models of spray combustion are based on the pure droplet diffusion combustion, such as the models proposed by Priem [4], and Gu [5], who studied the effect of droplet size on the completeness of spray combustion. Alternatively, a 1-D model proposed by Miesse [6] is based on the assumption of only unignited droplet evaporating in the gas flame with no droplet diffusion flames. Till now no models on two-mode spray combustion were reported.
For multi-dimensional CFD modeling of two-mode spray combustion, the combustion mode should be determined by the droplet ignition condition. Many years ago, Law [7,8] gave an asymptotic theoretical analysis for the droplet ignition criterion; the critical Damkohler number was obtained. His analysis is for the case of droplet burning in stagnant air without convection. The mathematical treatment is rather complex, including some numerical procedure. Subsequently, Wong, et al. [9] numerically studied the droplet ignition under forced convection based on a given gas flow field, assuming that the ignition at first occurs in the droplet wake. The ignition time lag and ignition distance were obtained. However, no ignition criterion was reported. Recently, Schnaubelt, et al. [10] did a detailed numerical simulation of droplet ignition with detailed reaction kinetics and no natural and forced convection, equivalent to microgravity condition. The ignition delay as a function of the ambient temperature was obtained. Stauch and Maas [11] also did detailed numerical simulation of a methanol droplet ignition under forced convection. The dependence of the ignition delay time on the droplet Reynolds number and the dependence of the location of the ignition point on the convective velocity of gas flow were obtained. Awasthi, et al. [12] studied the ignition delay times of heptane droplets using a 3-D full numerical simulation. No ignition limits were reported. A recent detailed review of theoretical and experimental studies on droplet ignition was given by Aggarwal [13], in which a comparison of theoretically predicted droplet ignition limits with measurement results is reported. For more accurate modeling two-mode spray combustion, it is necessary to find a simple droplet ignition model, which can be more conveniently incorporated into the numerical model of two-mode spray combustion.
In this paper at first a simplified 1-D model is given to explore the physics of the two-mode spray combustion. Secondly, a preliminary LES of spray combustion is made to learn the effect of some combusting droplets. Furthermore, a simplified droplet ignition model under forced convection using Frank-Kamenetsky's approximation for treating the highly nonlinear reaction term is proposed. Then, experimental studies on droplet ignition were reported to validate the droplet ignition model. Finally, more accurate modeling equations are suggested for future LES or RANS modeling two-mode spray combustion.
A Simplified 1-D Model of Two-Mode Spray Combustion
A simplified analysis using a 1-D model for the propagation of a two-mode spray flame is presented with a two-zone approximation. The schematic picture of a 1-D spray flame is given in Figure 1. It is assumed that the spray flame consists of five zones. At first the cold droplets enter the high-temperature gas zone, and then are preheated. Subsequently, the smaller droplets evaporate in high-temperature air to form combustible mixture with a pre-evaporation fraction Ψ1 and produce the gas flame, the larger droplets are ignited and produce the droplet diffusion flamelets, the pre-evaporated gas and the larger droplets are assumed to be simultaneously ignited, and produce a combined combustion zone, and later there are only droplet diffusion flamelets. Finally, there are combustion products. Neglecting the effect of droplet evaporation on the gas flow, the gas continuity equation is
The gas energy equations in the preheating zone and reaction zone are
The adiabatic boundary conditions at the cold and hot boundaries are
Where nd1 and nd2 are the number densities of ignited and un-ignited droplets. Pay attention that Equation (3) takes into account the heat release due to gas-phase premixed combustion and also the heat release due to droplet diffusion combustion, that is, for the case of two-mode spray combustion. Using the two-zone approximation method similar to that for single-phase laminar flame propagation by Frank-Kamenetsky [14], the propagation velocity of a two-phase turbulent flame is obtained as:
where Ψ1 is the pre-vaporization fraction ahead of the combustion zone, m is an experimental exponent, λT1 is the turbulent heat conductivity, ws* is the fictitious reaction rate for the case of full evaporation, τsf is the ignited-droplet life time, α is the coefficient of excess air, L0 is the stoicheometric ratio of air to fuel. The predicted two-phase flame propagation velocity is in agreement with the experimental results [15], as shown in Figure 2. This simplified analysis shows the physical mechanism of the two-mode spray combustion. It is seen that there is a minimum flame velocity at about the 20% of the pre-vaporization fraction (Figure 2a). For droplet sizes smaller than 100 µm, there is combined combustion of premixed gas-air flame and droplet diffusion flame, and for droplet sizes lager than 100 µm, there is only droplet diffusion combustion (Figure 2b).
A Preliminary LES of Spray Combustion Accounting for Some Ignited Droplets
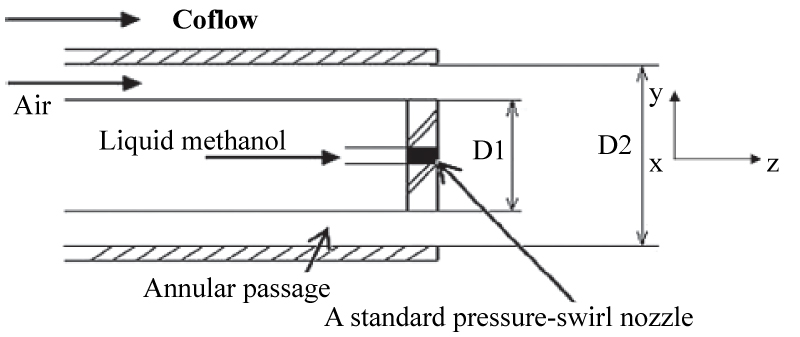
A preliminary LES of spray combustion was conducted to study the effect of ignited droplets on spray combustion. The controlling equations for Eulerian-Lagrangian LES are given like those for one-mode spray combustion. The filtered gas continuity and momentum equations for LES of two-phase combustion are
Where
The Smagorinsky SGS stress model and gradient modeling of SGS mass flux and heat flux, and the second-order moment SGS gas combustion model are adopted. In the source terms of these equations, the source terms due to the ignited droplets are taken into account. It is assumed that the droplets are ignited, if their lifetimes are greater than the ignition delay of the single-phase gas mixture, and the evaporation rate of both ignited and un-ignited droplets is under the same local gas temperature. The simulation was done for a methanol-air spray flame, as shown in Figure 3. For the numerical procedure, a third order MUSCL (Monotonic Up-Stream-Centered Scheme for Conservation Laws) scheme was applied for the species and energy equations, second-order scheme for pressure solution, bounded central differencing scheme for momentum equations and second-order scheme for temporal terms. The PISO algorithm for pressure-velocity coupling was adopted. The Lagrangian Discrete-Phase Model (DPM) was applied in the liquid-phase simulation with a pressure-swirl atomizer model for the methanol spray, the O'Rourke method for droplet collision, and the Taylor Analogy Breakup model for the droplets secondary breakup. The P1 radiation model was employed for radiative heat transfer. For boundary conditions, uniform gas inlet velocity, droplet inlet velocity with a spray angle and concentration are given according to experiments. No-slip condition for the gas phase is given at the boundary, and fully-developed flow condition is given at the exit. Random fluctuations are superposed to the inlet velocity. The predicted temperature distribution is shown in Figure 4, where the curves "FSM" denote the predictions accounting for the effect of ignited droplets, and the curves "KIM" denote the predictions not accounting for the effect of ignited droplets, and the curves "TM" denote the FLUENT prediction results. It is seen that the FSM predictions are somewhat better than other predictions; in particular it can give the two peaks of temperature observed in experiments (Figure 4a), whereas other predictions cannot do. The agreement between the FSM predictions and experiments is not very good, or sometimes its merits are not obvious (Figure 4b), because the assumption of a same gas temperature for the evaporation of both ignited and un-ignited droplets and the lack of an appropriate droplet ignition model caused obvious error.
A Droplet Ignition Model
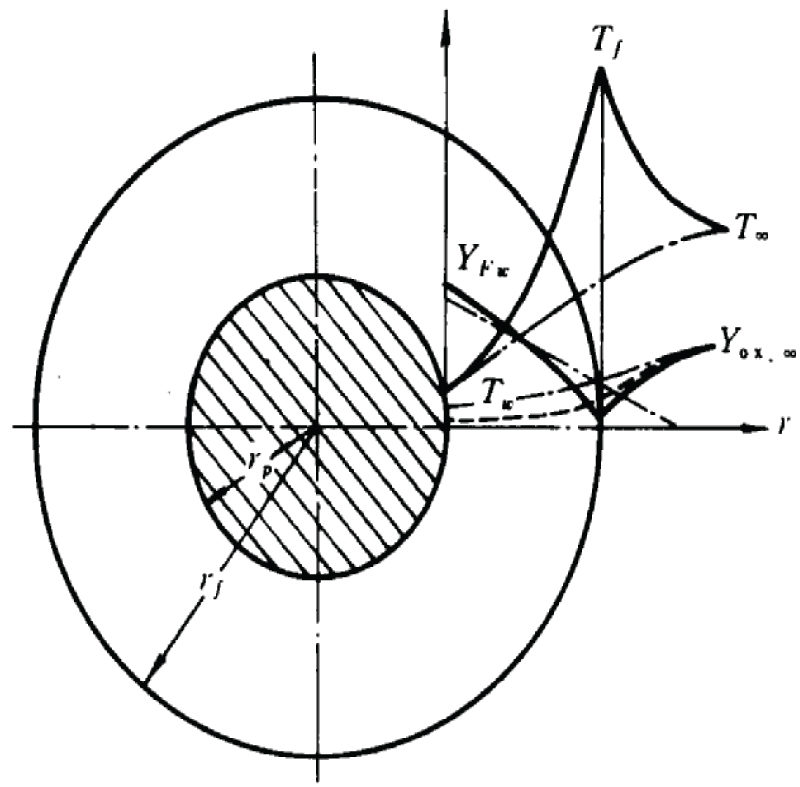
For more accurate CFD modeling of two-mode spray combustion, it is necessary to develop a droplet ignition model. A droplet ignition model under forced convection is proposed here. The initial state of the temperature and concentration distributions in the gas layer (stagnant gas film) surrounding the droplet under forced convection before ignition is shown as the dot-dashed lines in Figure 5. Consider the quasi-steady state of droplet evaporation. The effect of forced convection in the one-dimensional spherical model is taken into account by using the "stagnant film" approximation [16]. At first, it is assumed that the heat conduction in the stagnant film is equivalent to the droplet convective heat transfer (without evaporation and combustion) by setting
Then, we have
Here Nu* is the Nussult number for the droplet convective heat transfer without evaporation and combustion, known as the Ranz-Marshell formula
The continuity, species and energy equations in the stagnant film (the gas layer surrounding the droplet) are
Where cp denotes specific heat capacity, D denotes gas diffusivity, denotes evaporation rate, r denotes radial distance, v denotes gas velocity, ρ denotes gas density, p denotes pressure, Y denotes mass fraction, T denotes gas temperature, Q denotes reaction heat release, q denotes heat of evaporation, w denotes reaction rate respectively. The subscripts e, F, g, iner, ox, p, pr, w denote the values of evaporation, fuel, gas, inert species, oxygen, particle, products and wall respectively. The left-hand side terms of the species and energy equations are convection terms, and the right-hand side terms of these equations are diffusion terms and reaction terms.
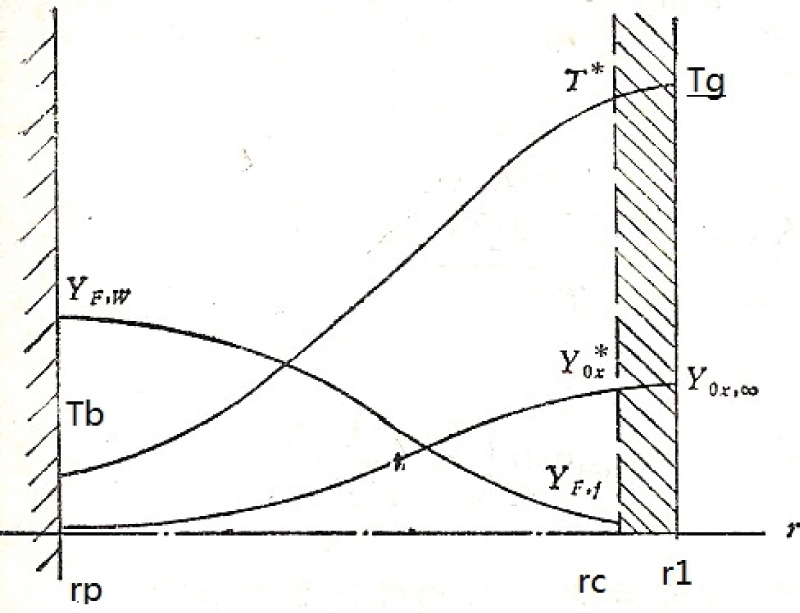
Using the Frank-Kamenetsky's approximation for treating the nonlinear reaction term [14], the gas layer (stagnant film) can be approximately divided into two parts: a very thin reaction layer and a pure heat transfer layer (Figure 6), and the thickness of the reaction layer is much smaller than that of the heat transfer layer. In the reaction layer rc < r < r1c adjacent to the hot boundary (Zone 1), where r1 is the radius of the stagnant film, rc is the inner radius of the reaction layer, the convection term in the energy equation in comparison with the reaction term can be neglected. In the heat transfer layer rp < r < rc (Zone 2), where rp is the droplet radius, the reaction term can be neglected. So, we have the following approximate energy equations in these two zones
for Zone1
Assume that ignition at first occurs at the hot boundary, use the Zeldovich criterion for thermal ignition at the hot surface [17]
Based on the information from the gas ignition experience, at the ignition moment the temperature at the inner boundary of the reaction zone can be approximately taken as
The averaged oxygen and fuel concentration in the reaction zone can be approximately taken as
Neglecting the change in the curvature of the very thin reaction zone, the energy equation is reduced to
Hence, integration of this energy equation in Zone 1 from rc to r1 gives
where the reaction rate is taken as a global one-step and second-order kinetics
The integral of the reaction term is approximately given by
Furthermore, integration the energy equation in Zone 2 from rp to rc gives
where the evaporation rate is
Therefore, we have
The coupling condition is the heat release due to reaction is equal to the heat transfer to the droplet surface, that is
Hence the droplet ignition criterion is obtained as
Finally, it can simply be expressed as
where A is an experimental factor, including the pre-exponential factor, the fuel concentration at the droplet surface and the oxygen concentration in the gas space outside the stagnant film. Considering the error of the simplified model, the pre-exponential factor A and the exponential factor n can be determined by experiments.
When
So, the droplet ignition model can be finally expressed by
Results and Discussion
Looking at the above-obtained theoretical results, it is seen that for unchanged for unchanged
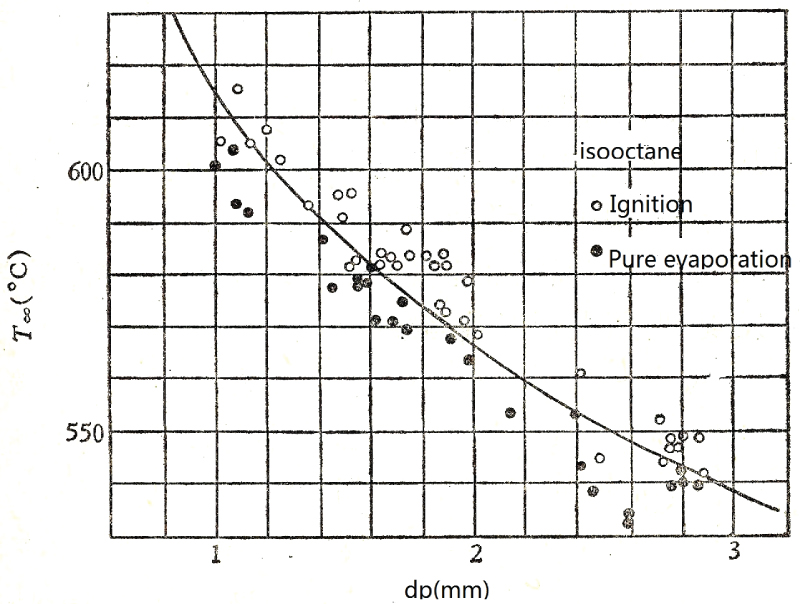
According to these theoretical results, the droplet ignition velocity is proportional to the droplet size, the droplet ignition temperature decreases with the increase of droplet size. These theoretical results are at first qualitatively compared with the experimental results reported in Ref. [13,18,19], as shown in Figure 7, Figure 8 and Figure 9. Figure 7 shows the ignition temperature decreases with the increase of the droplet size . Figure 8 indicates that the ignition temperature T∞ decreases with the increase of the droplet size dp. Figure 9 shows that the droplet ignition velocity v is proportional to the droplet size d. Hence the theoretical results give a right tendency. Recently, to validate the droplet ignition model, experiments were conducted in a combustion equipment of a suspended droplet [20]. The gas temperature was measured by a thermo-couple, the droplet size and ignition were recorded using a high-speed camera. The results give the comparison between the measured and modeled droplet ignition temperature vs. as the droplet size, and indicate that the agreement between model predictions and measurements is good. It implies that the proposed ignition model is quantitatively validated by experiments. These results will be published in the future.
The Suggested Model Equations of Two-Mode Spray Combustion
It is possible to more accurately study the two-mode spray combustion by LES or RANS modeling. For most cases, there exist simultaneous two modes of spray combustion: a mode of droplet diffusion combustion and a mode of unignited droplets evaporating in gas flames. For the first mode, the droplet burning will cause a sink in the oxygen concentration equation and a heat source in the gas energy equation. For the second mode, the droplet evaporation will cause a mass source in the fuel vapor concentration equation and an energy sink in the gas energy equation. The droplet ignition model is used to judge the spray combustion mode, and different evaporation models will be used for ignited and un-ignited droplets. The gas-phase continuity, momentum, energy and species equations for the two-mode spray combustion should be taken as
Where
Where
where nd1 and nd2 are the number densities of ignited and un-ignited or extinguished droplets respectively, and are the evaporation rates of burning and un-burning droplets respectively, β is the stoichiometric coefficient of oxygen to fuel, ws is the gas reaction rate relative to species s, Qd is the convective heat transfer between the gas and droplets, Qf, Qs are the reaction heat release relative to species f and s respectively, qe is the evaporation latent heat, and qr is the gas radiative heat transfer. The number densities nd1 and nd2 are judged by the droplet ignition model, given in the following text.
In the frame of Eulerian-Lagrangian approach, the droplet equations should be taken as
Continuity
Momentum
Energy
Mass Change
As above indicated, for the unchanged fuel properties and oxygen concentration, the droplet ignition condition can be given as:
For most cases Nu* ≫ 2, and the droplet ignition condition reduces to
where A is an experimental constant, including the pre-exponential factor, fuel heating value and oxygen concentration in chemical kinetics. So, the droplets with larger sizes and smaller relative gas velocities will be ignited and have the number density nd1, and droplets with smaller sizes and larger relative gas velocities will not be ignited or extinguished and have the number density of nd2. The judgment is
When Droplets will be ignited, and are included in the part of nd1, the spray combustion is in the mode of droplet diffusion flame.
When Droplets will not be ignited or be extinguished, and are included in the part of nd2 , the spray combustion is in the mode of cold droplets evaporating in the gas flame.
The Suggested Solution Procedure
The solution procedure should be as follows:
(1) At first account for only cold droplets evaporating in gas flames, neglect droplet ignition, put nd1 = 0 in the two-phase equations, do the computation of two-phase flows and combustion to give local gas temperature, droplet sizes and relative velocities.
(2) Based on the local gas temperature, droplet sizes and relative velocities obtained in the first step and using the droplet ignition condition, determine the number densities and the positions of burning and un-burning droplets.
(3) Then, put the source terms due to droplet burning into the two-phase equations to compute the two-phase flows and combustion once again.
(4) Repeat the computation for several times to get the final results.
Conclusions
(1) A 1-D model of spray flame propagation is presented to show the physics of two-mode spray combustion.
(2) A preliminary LES of spray combustion was made to show the effect of ignited droplets on the spray combustion.
(3) A droplet ignition model was developed for its application in modeling of two-mode spray combustion, and is validated by recent experiments done by the authors.
(4) More accurate model equations of two-mode spray combustion are suggested for future RANS modeling, LES and point-particle DNS of two-mode spray combustion.
Acknowledgement
This study was sponsored by the National Natural Science Foundation of China under the Grants 51390493, 51106006 and 51266008.