International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 2, Issue 2
Review Article
DOI: 10.35840/2631-5009/7509
Analysis of Accelerating Devices for Enclosure Wind Turbines
Ahmad Sedaghat1*, Rafat Al Waked2, M El Haj Assad3, Khalil Khanafer1 and Muath NA Bani Salim1
Figures

Figure 3: The four sided (left) and...
The four sided (left) and eight sided (right) wind catchers in Dowlat-Abad house and garden in the city of Yazd [34/a>].
Figure 5: Hollow circular devices tested...
Hollow circular devices tested in wind tunnel by Ohya, et al. [13].
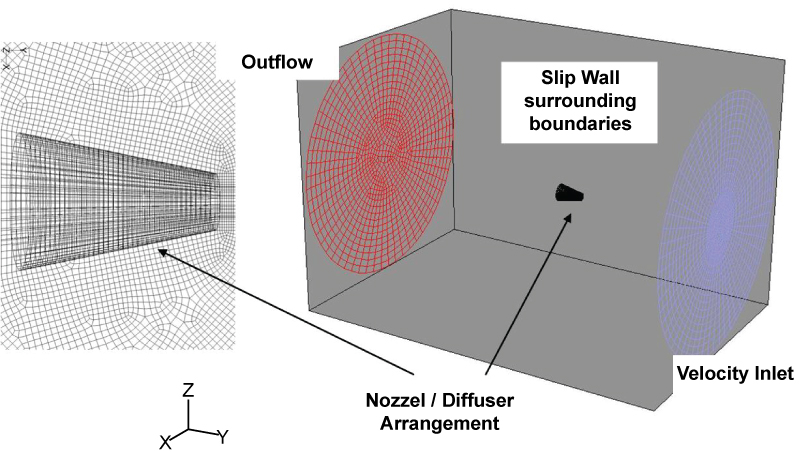
Figure 6: General view of the utilised CFD...
General view of the utilised CFD model showing boundary types and mesh elements.
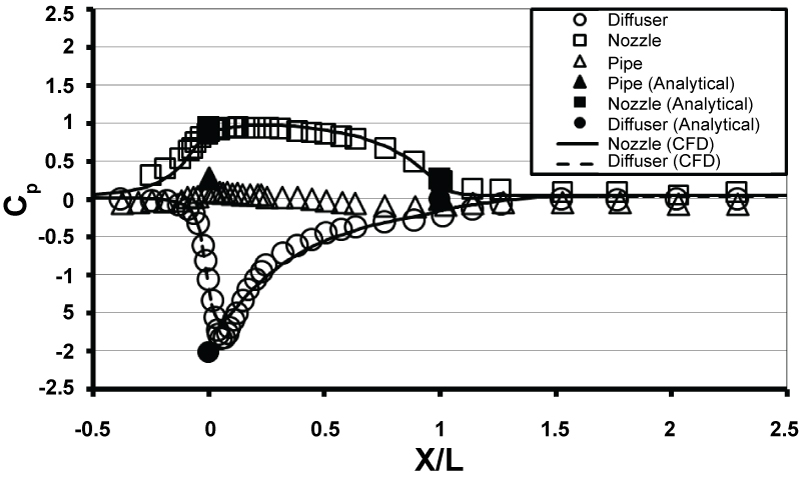
Figure 8: Comparison of CFD, analytical...
Comparison of CFD, analytical and experimental centre line pressure coefficient along hollow circular pipe, nozzle, and diffuser with L/D = 7.7 and area ratio of 1, 4, and 1/4, respectively (nonsolid symbols from experiments by Ohya, et al. [13]).
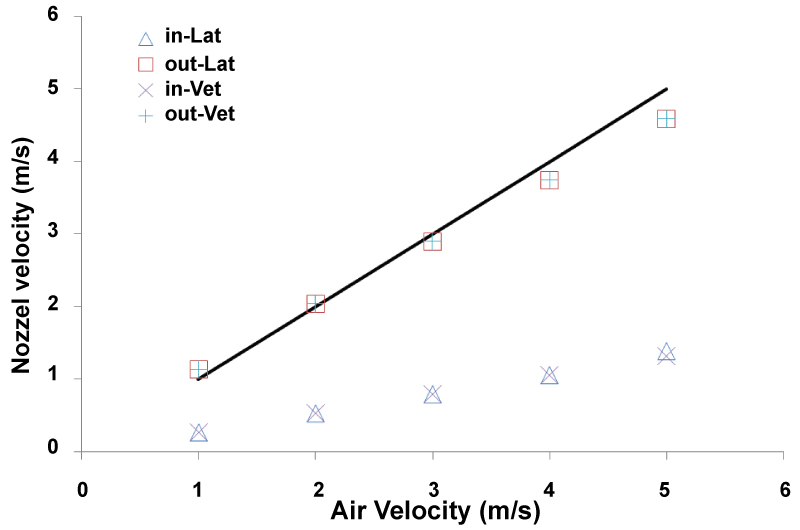
Figure 9: Wind velocity in lateral...
Wind velocity in lateral and vertical directions at inlet and outlet of the nozzle with L/D = 3.4 and area ratio of 6.
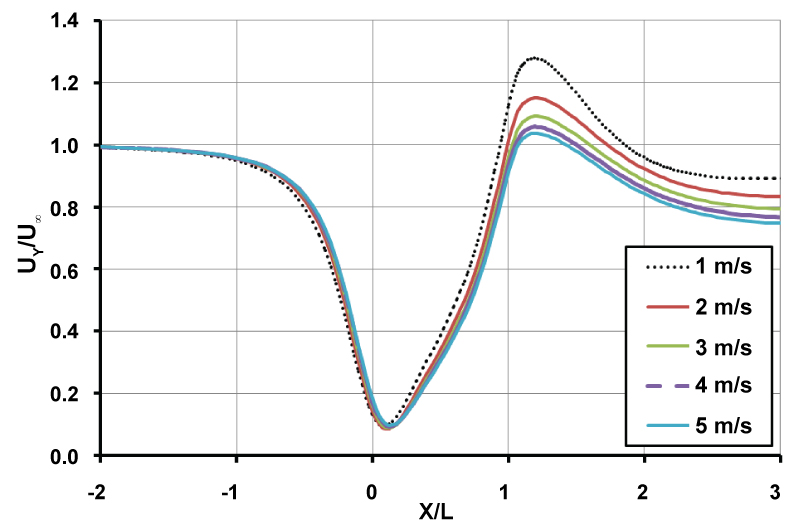
Figure 10: Centre line wind velocity in...
Centre line wind velocity in the vertical nozzle with L/D = 3.4 and area ratio of 6 at different free stream velocities.
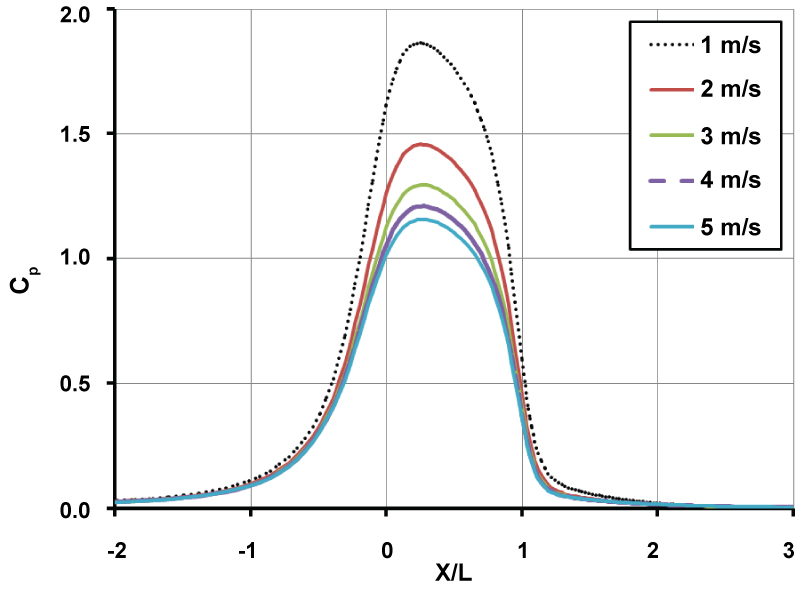
Figure 11: Centre line pressure coefficient...
Centre line pressure coefficient distribution in the vertical nozzle with L/D = 3.4 and area ratio of 6 at different free stream velocities.
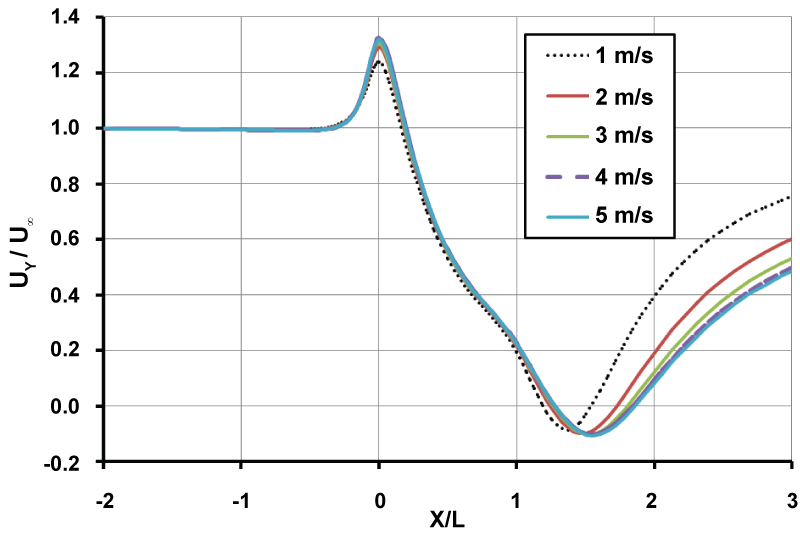
Figure 12: Centre line wind velocity in the...
Centre line wind velocity in the vertical nozzle with L/D = 3.4 and area ratio of 6 at different free stream velocities.
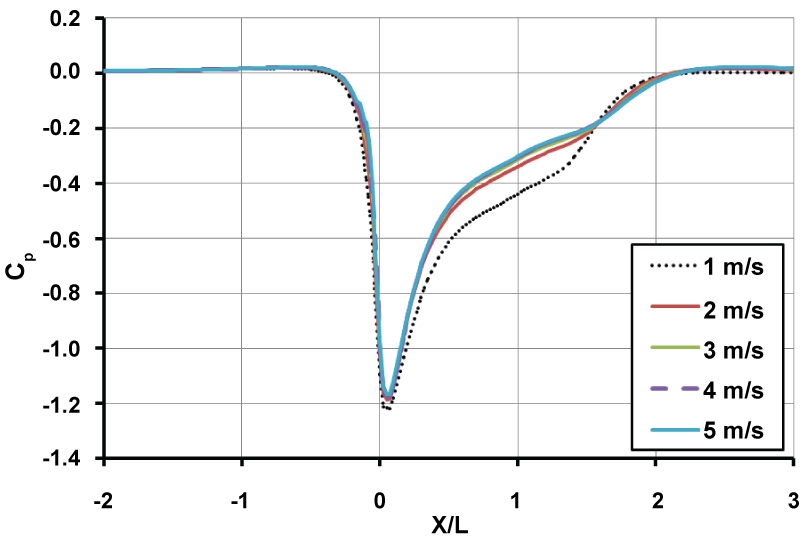
Figure 13: Centre line pressure coefficient...
Centre line pressure coefficient distribution in the vertical diffuser with L/D = 3.4 and area ratio of 6 at different free stream velocities.
References
- O Igra (1976) Design and Performance of a Turbine Suitablefor an Aerogenerator. Energy Conversion 15: 143-151.
- O Igra (1981) Research and development for shrouded wind turbines. Energy Conversion Manage 21: 13-48.
- BL Gilbert, KM Foreman (1983) Experiments with a diffuser-augmented model wind turbine. J Energy Res Technol 105: 46-53.
- CAJ Fletcher (1981) Computational analysis of diffuser-augmented wind turbines. Energy Conversion Manage 21: 175-183.
- M Nagai, K Irabu (1987) Momentum theory for diffuser augmented wind turbine. Trans JSME 53: 1543-1547.
- ML Helmy (1991) Dimensions of the axial flow turbine design for wind power. Renewable Energy 1: 303-307.
- DG Phillips, PJ Richards, RGJ Flay (2000) CFD modelling and the development of the diffuser augmented wind turbine, Proceedings of the Comp, Wind Eng, Birmingham, 189-192.
- MOL Hansen, NN Sorensen, RGJ Flay (2000) Effect of placing a diffuser around a wind turbine. Wind Energy 3: 207-213.
- F Bet, H Grassmann (2003) Upgrading conventional wind turbines. Renewable Energy 28: 71-78.
- Y Ohya, T Karasudani, A Sakurai, M Inoue (2002) Development of high-performance wind turbine with brimmed diffuser. J Japan Soc Aeronaut Space Sci 50: 477-482.
- Y Ohya, T Karasudani, A Sakurai, M Inoue (2004) Development of high-performance wind turbine with abrimmed-diffuser: Part 2. J Japan Soc Aeronaut Space Sci 52: 210-213.
- K Abe, M Nishida, A Sakurai, Y Ohya, H Kihara, et al. (2005) Experimental and numerical investigations of flow fields behind a small wind turbine with a flanged diffuser. Journal of Wind Engineering and Industrial Aerodynamics 93: 951-970.
- Y Ohya, T Karasudani, A Sakurai, Ken-ichi Abe, Masahiro Inoue, et al. (2008) Development of a shrouded wind turbine with a flanged diffuser. Journal of Wind Engineeringand Industrial Aerodynamics 96: 524-539.
- Y Ohya, T Karasudani, X Zhang (2008) A new wind turbine with wind-lens technology and its application to an irrigation plant in a desert area in China, 2nd Joint seminar Kyushu University and Bordeaux University, Fukuoka, Japan, 10-11.
- Y Ohya, T Karasudani (2010) A Shrouded Wind Turbine Generating High Output Power with Wind-lens Technology. Energies 3: 634-649.
- T Matsushima, S Takagi, S Muroyama (2006) Characteristics of a highly efficient propeller typesmall wind turbine with a diffuser. Renewable Energy 31: 1343-1354.
- F Wang, L Bai, J Fletcher, J Whitefordc, D Cullenc (2008) Development of small domestic wind turbine with scoop and predictionof its annual power output. Renewable Energy 33: 1637-1651.
- F Wang, L Bai, J Fletcher, J Whitefordc, D Cullenc (2008) The methodology for aerodynamic study on a small domestic wind turbine with scoop. Journal of Wind Engineeringand Industrial Aerodynamics 96: 1-24.
- A Grant, C Johnstone, N Kelly (2008) Urban wind energy conversion: The potential of ducted turbines. Renewable Energy 33: 1157-1163.
- SY Hua, JH Cheng (2008) Innovatory designs for ducted wind turbines. Renewable Energy 33: 1491-1498.
- TY Chen, YT Liao, CC Cheng (2012) Development of small wind turbines for moving vehicles: Effects of flanged diffusers on rotor performance. Experimental Thermal and Fluid Science 42: 136-142.
- B Kosasih, A Tondelli (2012) Experimental study of shrouded micro-wind turbine. Procedia Engineering 49: 92-98.
- SAH Jafari, B Kosasih (2014) Flow analysis of shrouded small wind turbine with a simple frustum diffuser with computational fluid dynamics simulations. J Wind Eng Ind Aerodyn 125: 102-110.
- J Gao, Q Zheng, X Jia (2014) Performance improvement of shrouded turbines with the management of casing endwall interaction flows. Energy 75: 430-442.
- http://www.weatherbase.com/weather
- http://www.ace.mmu.ac.uk/eae/Climate/ Older/Desert_Climate.html
- MN Bahadori (1994) Viability of wind towers in achieving summer comfort in the hot arid regions of the Middle-East. Renewable Energy 5: 879-892.
- GS Battle, M Zanchetta, P Heath (2000) Wind towers and wind driven ventilation. In: AAM Sayigh, World Renewable Energy Congress VI. (1st edn), Elsevier, Brighton, England, 432-437.
- AA Elmualim (2004) Modeling of a wind catcher for natural ventilation. In: AAM Sayigh, World Renewable Energy Congress VIII. National Renewable Energy Laboratory, Colorado, USA.
- AA Elmualim (2006) Effect of damper and heat source on wind catcher natural ventilation performance. Energy and Buildings 38: 939-948.
- Ali Mostafaeipoura, Behnoosh Bardela, Kasra Mohammadib, Ahmad Sedaghatc, Yagob Dinpashohd (2014) Economic evaluation for cooling and ventilation of medicine storage warehouses utilizing wind catchers. Renewable and Sustainable Energy Reviews 38: 12-19.
- C Karakatsanis, MN Bahadori, BJ Vickery (1986) Evaluation of pressure coefficients and estimation of air flow rates in buildings employing wind towers. Solar Energy 37: 363-374.
- A Sharag Eldin (1994) Wind direction sensitivity analysis of wind towers. The 19th National Passive Solar Conference.
- A Mostafaeipour (2005) Method of Capturing Wind in an Old City of Yazd in Iran. 4th World Wind Energy Conference, Australia.
- H Montazeri (2011) Experimental and numerical study on natural ventilation performance of various multi-opening wind catchers. Building and Environment 46: 370-378.
- V Kalantar (2009) Numerical simulation of cooling performance of wind tower (Baud-Geer) in hot and arid region. Renewable Energy 34: 246-254.
- MN Bahadoria, M Mazidib, AR Dehghani (2008) Experimental investigation of new designs of wind towers. Renewable Energy 33: 2273-2281.
- M Kazemi Esfeh, AA Dehghan, M Dehghan Manshadi, S Mohagheghian (2012) Visualized flow structure around and inside of one-sided wind-catchers. Energy and Buildings 55: 545-552.
- D Allaei, Y Andreopoulos (2014) INVELOX: Description of a new concept in wind power and its performance evaluation. Energy 69: 336-344.
- Abdel moniem El Shorbagy (2010) Design with nature: windcatcher as paradigm of natural ventilation device in buildings. IJCEE 10.
- Gerard JW van Bussel (2007) The science of making more torque from wind: Diffuser experiments and theory revisited. J Phys 75.
- KH Wong, WT Chong, NL Sukiman, SC Poh, YC Shiah, et al. (2017) Performance enhancements on vertical axis wind turbines using flow augmentation systems: A review. Renewable and Sustainable Energy Reviews 73: 904-921.
- L Chen, FL Ponta, LI Lago (2011) Perspectives on innovative concepts in wind-power generation. Energy for Sustainable Development 15: 398-410.
- C Shonhiwa, G Makaka (2016) Concentrator Augmented Wind Turbines: A review. Renewable and Sustainable Energy Reviews 59: 1415-1418
- BR Munson, WW Huebsch, AP Rothmayer, Theodore H Okiishi (2012) Fundamentals of Fluid Mechanics. (7th edn), Wiley.
- http://www.ansys.com/Products/Simulation +Technology/Fluid+Dynamics/Fluid+ Dynamics+Products/ANSYS+Fluent
Author Details
Ahmad Sedaghat1*, Rafat Al Waked2, M El Haj Assad3, Khalil Khanafer1 and Muath NA Bani Salim1
1School of Engineering, Australian College of Kuwait, Mishref, Kuwait
2German Jordanian University, Jordan
3SREE Department, University of Sharjah, United Arab Emirates
Corresponding author
Ahmad Sedaghat, School of Engineering, Australian College of Kuwait, Mishref, Kuwait, E-mail: [email protected]
Accepted: August 04, 2017 | Published Online: August 07, 2017
Citation: Sedaghat A, Waked RAI, Assad MEIH, Khanafer K, Salim MNAB (2017) Analysis of Accelerating Devices for Enclosure Wind Turbines. Int J Astronaut Aeronautical Eng 2:009.
Copyright: © 2017 Sedaghat A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
There are fundamental differences between internal and external flows over short hollow devices. For internal flows, the outflow velocity in a pipe with constant cross section is unchanged, in a nozzle is accelerated, and in a diffuser is retarded. This is tempting for general wind turbine practitioners to develop enclosure type wind turbines for accelerating wind speed and augmenting wind power. In this study, the short hollow accelerating devices without interaction of wind turbines is investigated in vertical orientation using analytical and CFD (Computational Fluid Dynamics) techniques. The literature on shrouded wind turbines and wind catchers are briefly reviewed. Bernoulli energy equation are used to derive some simple analytical formulations considering viscous losses to determine inlet and outlet pressure and velocity along centreline of three short hollow devices of tube, nozzle, and diffuser shapes in external flows. Then, CFD simulations are carried out for the hollow devices in both horizontal and vertical orientation. The results of computational and analytical methods indicate that the wind speed at the inlet of nozzle retarded due to development of a pressure zone, in good agreement with the experimental data, and the outlet flow velocity is slightly increased compared with the free stream inlet velocity at low wind speeds. Flow simulations around diffuser device however reveal a suction zone at the inlet where intake of air improves and the intake air velocity is increased compared with free stream inlet air velocity particularly at higher wind speeds. No noticeable differences are observed between flow features around horizontal and vertical accelerating devices. It is concluded that for vertical enclosure wind turbines, the diffuser shape of the enclosure particularly at the section with a wind turbine may be more suited in agreement with the proven concepts of shrouded wind turbines and wind catcher.
Keywords
Nozzle and diffuser, External flow, Enclosure wind turbine, Computational Fluid Dynamics (CFD), Wind catcher
Introduction
From the classical fluid mechanics it is well known that nozzles accelerate and diffusers decelerate steady internal flows with constant mass flow rate. In such devices, the outlet to inlet velocities will be proportion to the ratio of inlet and outlet areas; hence, there would be appreciable conversion factor for these fluid devices. For example, in design of wind tunnels, nozzles and diffusers with the area ratio of six and two, respectively, are in common use. This means such nozzles accelerate outlet flow velocity by six times and diffusers decelerate outlet velocity by two times. For wind turbine designers, these devices are very attractive because the wind power is proportional to cube of wind velocity. For example, a nozzle with the area ratio of six enhances the wind power by a factor of 36. Therefore, many researcher and scientists exploited different approaches to develop and design wind turbines by devices to accelerate wind velocity at rotor plane. Because of fundamental differences of external flows over nozzles and diffusers compared with internal flows, a large number of literatures focuses on diffuser or shrouded wind turbines. The orientation of accelerating devices within shrouded wind turbines were mainly horizontal for improvement of horizontal axis wind turbines; but, no study were conducted to study the flow accelerating devices in vertical orientation. With recent growth interest in using wind catchers in architects of modern buildings and applications of renewable energies, there is opportunity to develop wind generators within wind catcher architecture.
Backgrounds in shrouded wind turbines
Research works exploiting applications of wind turbine inside shrouded aero generator may be dated back as early as 1976 when Igra [1] built and tested two wind turbines in wide range of axial and angular inlet velocities for several numbers of blades. His investigation also included wind turbine design in enclosures which indicated that his simple model can be used for design of shrouded wind turbines. His experiments for a load factor below 0.3 showed good agreement with his model for a range of solidity factor (1.57 ≤ σ ≤ 6.28). Eventually he observed that for low load factors (below 0.3) the number of blades above 6 will not improve power performance. Igra [1] also summarized that for higher load factors the viscous effects should be incorporated within his model and for higher Reynolds number than narrow band of his experiments (105 ≤ Re ≤ 2.6 × 105) from similarity laws the power performance can be better. A relatively constant power capture for wide range of a velocity factor reported. Igra [2] reported research and development of shrouded wind turbines with significant power augmentation using a compact shroud and up to 80% extra power improvement by using ring shape flaps while additional 25% enhancement were also observed using appropriate bleeding from exterior of shroud. He also presented design of the axial wind turbine for the proposed shroud. A pilot wind turbine with 1 hp power at 5 m/s with 3 meters in diameter were built and its field test results were compared with models (Figure 1). He reported measurements of wind power which shows augmentation of two times compared with shroud less wind turbine. The power augmentation was related to two important factors: the in viscid wake recovery causing subatmospheric pressure at the shroud exit plane and the kinetic energy conversion into pressure in the rear part of diffuser. From economical point of view also the given concept proved to be more efficient than conventional wind turbines.
The new idea of using diffuser assisted wind turbine spread in US, Japan, and Europe. In US, Gilbert Foreman [3] conducted experiments with a diffuser-augmented model of wind turbine in 1983.
From 1981 forward, attention was also drawn more in mathematical and computational modelling of shrouded wind turbines. Fletcher [4] has used blade element computational method on diffuser augmented wind turbines including wake rotation and blade Reynolds number effects. His computational results matched well with some experiments on power coefficient and axial velocities. Maximum power augmentation of four times was reported using solidity factor of 0.1 ≤ σ ≤ 0.15 depending on the aerofoil section used for the wind turbine blades. Nagai and Irabu [5] have also developed the momentum based theory for diffuser augmented wind turbine in Japan.
Helmy [6] further developed theoretically shrouded wind turbines assisted with rear edge flanged diffuser. His studies revealed that power coefficient was doubled and he suggested optimal dimension of diffuser and the flange. In parallel in UK and Denmark, Phillips, et al. [7] used CFD modelling and the development of the diffuser augmented wind turbine and Hansen, et al. [8] studied effect of placing a diffuser around a wind turbine. Bet and Grassmann [9] studied computationally two diffuser rings around the wind turbine rotor and reported that by creating a field of low pressure behind the wind turbine the power coefficient was doubled.
Later in Japan, Ohya, et al. [10,11] have developed a diffuser-flanged shroud system around small wind turbines. The flanged-diffuser shroud job was to collect and accelerate the free stream wind. The flange at the exit of the diffuser shroud generated a low-pressure region in the wake region of the diffuser by vortex formation and entraining more air into the wind turbine inlet. The shrouded wind turbine was optimized for which wind power augmentation of about 4-5 times is reported compared with the bare wind turbine.
Abe, et al. [12] have carried out an extensive experimental and numerical study on the same wind turbine with a flanged diffuser of Ohya, et al. [10,11] (Figure 2). They observed four times augmentation of wind turbine power coefficient using both hot-wire anemometry measurements and computations. In addition, they noticed when the power performance of diffuser-flanged was normalized by a mean velocity behind blades, both the bare and diffuser-shrouded wind turbines presented similar performances. Thus, they conclude that in both situations the wind turbine operates similarly and the power augmentation was mainly related to the acceleration of approaching air by the flanged diffuser. Wind tunnel experiments and filed measurements indicated that the output performance was as expected.
In 2008, Ohya, et al. [13] have developed their optimized diffuser shroud wind turbine with a broad-ring flange (Figure 2) at the exit of diffuser. Their emphasis was on placing the exit flange dimension and position so that a low-pressure region generated behind of the wind turbine in the wake of rotor where a strong tip vortex formation and interaction occur inside the diffuser. Their optimal design claimed to produce 4 to 5 times more power compared with their bare wind turbine (500 W). Both wind tunnel tests and field tests performed as expected. Ohya, et al. [14,15] introduced a new diffuser design with a broad-ring brim at the exit in several compact dimensions. Two to five times wind power augmentation was achieved using new compact designs due to low-pressure region mainly produced by strong vortex formation behind the broad brim. This brings more mass flow rate to the wind turbine inside the diffuser shroud.
In another work, Matsushima, et al. [16] studied a similar diffuser-flanged wind turbine using field testing and also computation of the bare diffuser-flanged without wind turbine. From computation, they reported the maximum increase of wind speed by a factor of 1.7 of the free stream velocity using appropriate diffuser length and expansion angle. They also reported fastest air speed near the inlet of diffuser. The field test results also confirmed that the wind power increased by up to 2.4 times compared with the bare wind turbine. They however argued that their numerical results overestimated the maximum wind speed ratio and output power of 1.7 and 5, respectively, compared with measured values. Therefore, they suggested that their wind turbine had negative effects when introduced to the diffuser or the frequent and rapid changes in wind speed and wind direction has caused the discrepancy leading lower performance of the wind turbine generator than computed optimal one.
In UK, Wang, et al. [17,18] reported on aerodynamic design of a small urban wind turbine with scoop. CFD simulations of the wind turbine and detailed design for blades, nosecones and nacelles were given. Estimation of the annual power output of this wind turbine calculated using hourly wind data of Scottish Weather Station was compared with other commercial turbines and reported as rather competitive. The final design of the scoop wind turbine boosted wind speed and power output by a factor of 1.5 and 2.2 times, respectively, compared with the bare wind turbine of same swept area confirmed also by wind tunnel tests. The results also indicated that power capture improved particularly at locations where average wind speed was lower and wind was more turbulent. Grant, et al. [19] also considered urban wind power using a roof-mounted ducted wind turbine to use pressure difference by wind flow around a building in UK. A simple mathematical model presented and compared with outcomes from tests at model and prototype scale. It was concluded that ducted turbines have, for in the most promising applications, power coefficients well in excess of the conventional Betz limit. Another advantage was low visual impact and safety.
In Taiwan, Hua and Cheng [20] designed a vertical bucket-shape ducted wind turbine. They argued that conventional ducted wind turbines required large inlets to absorb more mass flow rate; however, the task should be increasing the speed of wind. They optimized geometry of the ducted wind turbine using object-oriented optimization and CFD simulations. The optimal shape of their duct appeared to be an unconventional nozzle, which increased wind speed by 60%. The results of their field tests of their prototype ducted wind turbine showed power augmentation of 1.6 to 1.8 times the bare wind turbine. Chen, et al. [21] also developed a shrouded, small, horizontal-axis wind turbine installing on moving vehicles. They studied the effects of flanged diffusers on rotor performance of a small (30 cm rotor diameter) wind turbine with different rotor solidities (20-60%) and wind speeds (10-20 m/s). Wind tunnel experiments confirmed that the flanged diffuser may significantly increase the power output of the wind turbine for higher solidity of 30% to 40% and low wind speeds. Their study also showed that a small wind turbine has the characteristics of low torque and high rotational speed, and high rotor solidity for maximum power output compared to a conventional large wind turbine.
In Australia, Kosasih and Tondelli [22] studied shrouded micro-wind turbine by examining diffuser shape and geometries, blade airfoils, and wind condition of a mounting site. The effect of different configurations namely: straight diffuser, nozzle-diffuser combination, and diffuser-brim combination were investigated. Test results confirmed that straight diffuser improved wind turbine performance by 60%, the nozzle-diffuser enhancement of 63%, and brimmed diffuser also improved performance. Increasing the diffuser length (L/D) did not affect the optimum Cp of the wind turbine but shifted the performance curve and the optimum Cp to higher tip-speed-ratio. But adding brim (flange) at the exit plane of the diffuser increased the performance, Cp as well as reduced the cut in speed and shifted optimum to higher value. Jafari and Kosasih [23] also reported experimental and Computational Fluid Dynamic (CFD) studies for diffuser shrouded an AMPAIR300 wind turbine which demonstrated significant power augmentation. Their studies showed strong dependency on the shape and dimensions of the diffuser. Different diffuser shapes and dimensions were investigated to understand their effects on power augmentation. From the CFD results, sub-atmospheric back pressure is found to be the most influential factor in power augmentation. It was argued that flow separation on the diffuser surface led to significant reduction in the pressure recovery coefficient and so the overall power augmentation.
Gao, et al. [24] have computationally studied internal unsteady flow in a 1.5-stage shrouded turbine with straight and bowed vanes. Their aim was to control of casing end wall secondary flows and losses due to unsteadiness effects. Their results show that the interaction with upstream bowed wakes has a beneficial effect on casing end wall flow behaviour resulting in weakening secondary flows. The combined unsteady effects on turbine performance depend on the balance of unsteady end wall mixing and end wall secondary flows and the negative impact of these effects should be alleviated to achieve enhanced performance.
Review of wind catchers
Wind catchers (Badgirs) are important infrastructure part of the Iranian traditional architecture for supplying natural conditioned air to buildings in both dry hot and humid hot weather conditions for thousands of years. The wind catchers not only used for air ventilation of buildings but also used for cooling in water cisterns (Ab-anbar) [25,26]. The natural ventilation of buildings is the tradition of ancient Persia buildings to allow wind entry from tall towers for cooling and conditioning air above a basement pond into rooms and hall of building. The wind catchers are widely used in architecture of desert type buildings in the central and the southern parts of Iran and are known as Bawdgir [27-30]. The wind catchers configurations are varied among one sided, two sided, four sided and eight sided towers. The design of the wind catcher is varied from one city to another city. For example, the design of wind catchers in the city of Yazd are taller with four to eight sided configuration compared with the nearby city of Maybod with lower height and one sided types [31]. The reason for this difference may be related to the fact that Yazd city is located among mountains with weak winds while Maybod is located in a flat desert with frequent strong dust storms. In general, wind catchers with short and one sided designs or tall and with four to eight sided designs are widely adapted to suit air conditioning of building in different meteorological conditions.
The wind catchers are traditionally built for heights from just 2 meters to 20 meters or higher on top of buildings using wood-reinforced masonry constructed by clay and sun dried clay bricks. Some authors suggest that taller towers capture higher wind speeds with lower dust entry [27,30,32,33].
Figure 3 shows a typical four and eight sided wind catcher in Dowlat-Abad house and garden in the city of Yazd. The house was built in the 18th century and was once the home of the Persian regent, Karim Khan Zand [34].
Recently, many researches were conducted to assess operation and performance of wind catchers in Iran. Montazeri [35] has investigated wind catchers with different number of opening using smoke visualization and computational techniques. His results suggest that the crucial parameter in performance of the studied wind catchers is the number of openings. Kalantar [36] research in the city of Yazd showed that the evaporative cooling is the main cooling mechanism in this dry hot city and he suggested equipping the wind catchers with the water vaporization system to reduce considerably air temperature inside buildings. Bahadori, et al. [37] investigated two new designs for wind catchers, with wetted column and wetted surfaces, and compared their performances with a conventional wind-catcher in the city of Yazd. The two new designs have improved temperature reduction and increased relative humidity compared with traditional one.
Kazemi Esfeh, et al. [38] applied smoke visualization to assess wind catcher models with flat, inclined and curved roofs. His study showed superior performance using the wind catcher with a curved roof.
Development of an enclosure wind turbine
Most recently in US, Allaei and Andreopoulos [39] have introduced the new concept of enclosure wind turbines, namely INVELOX (Figure 4). The innovative feature of INVELOX is by combining wind tunnel and wind catcher systems to capture wind flow through a vertical enclosure intake and hence eliminating the need to yaw control. The flow accelerates through a shrouded Venturi and exhaust into atmosphere by a diffuser.
CFD simulations and field testing were conducted to evaluate performance of this wind turbine. The results of their studies showed that it is possible to capture, accelerate and concentrate the wind. The total average wind power augmentation of INVELOX over 8 days was reported about 314% compared with bare wind turbine. The cut-in wind speed of 1 m/s is promising for development of enclosure wind turbines integrated within wind catcher designs for low speed regions in hot deserts.
The Allaei's idea seems to stem on the concept of wind catcher designs which used to generate natural cooling comfort through drift of wind into building. Wind catchers considered as the tradition of Persian architecture which was developed and used for many centuries. However, there is a fundamental difference between Allaei's model as shown in Figure 4 and the traditional wind catchers. As seen in Figure 3, the wind is drawn into a big space from a uniform cross section canal. This is more likely act as a diffuser than a nozzle. The openings of the wind catcher are narrow and much smaller compared with room space where wind is drawn. Therefore, the above literature of research on diffusers and the proven concept of wind catchers may suggest that a enclosure wind turbine should utilize a diffuser to collect and expand air into the designs such as INVELOX and then the concentrated wind should be accelerated in a contraction nozzle and an expanding diffuser (or Venturi) similar to design of blower wind tunnels to augment wind speed. The advantage of such design compare with Ohya's diffuser assisted horizontal wind turbine is that the wind can enter into the structure from any directions without the need for yaw mechanism control. Design of enclosure wind turbine can also integrate with wind catchers to be incorporated in architecture of modern buildings with natural air conditioning systems [31,40].
Bussel [41] have reviewed 50 years of Diffuser Augmented Wind Turbines (DAWTs). Bussel concluded that using 1D momentum theory power extracted from a DAWT is the same as a bare wind turbine. He reported that power augmentation beyond 3 has never achieved. However, Wong, et al. [42] reviewed various flow augmentation methods for the purpose of utilizing with Vertical Axis Wind Turbines (VAWTs) and reported large magnification of 9 times output power. Chen, et al. [43] has reviewed innovative wind turbine concepts. They believe the main challenges of new innovative wind turbines are not only augmentation of power but also economical and environmental friendly aspects of designs. Shonhiwa and Makaka [44] has reviewed the concept of Concentrator Augmented Wind Turbine (CAWT). They found that the best concentrator should locate 5 cm in front of the wind turbine and it should be a nozzle shape with inlet to outlet ratio of 6.
The aim of present study is to exploit external flows over vertical accelerating devices such as nozzles and diffusers for application in such wind generators. The paper is outlined as to give a background study on shroud-diffuser wind power augmentation followed by theoretical modelling of the accelerating devices. Then, the results of mathematical modelling are compared with results of CFD simulations and some available experimental data on horizontal axis accelerating devices. Next, computational results are presented for vertical nozzle and diffusers at wide range of wind speeds. Finally, conclusions and guidelines are provided for future development of vertical accelerating devices in enclosure wind generating systems.
Mathematical Modelling
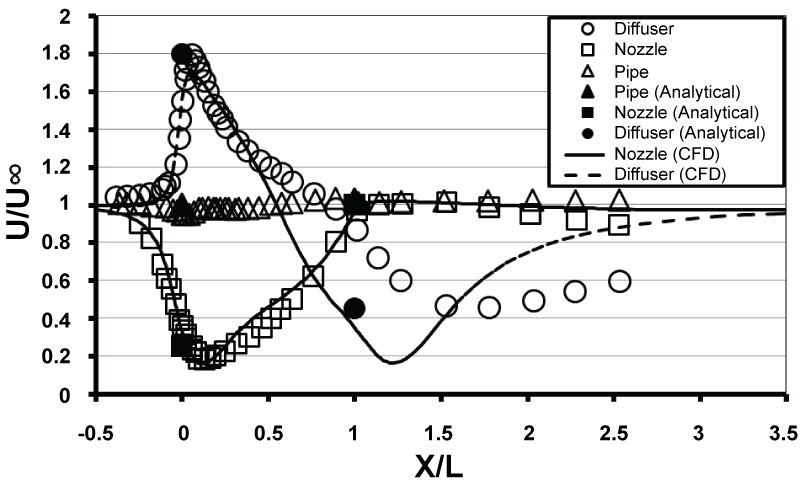
Literature discussed above has merely reflected on simple models for wind turbine integrated with shroud diffusers. Some authors suggested that the main cause of power augmentation was due to shroud diffuser and others considered interaction between wind turbine and shroud was responsible for this. Ohya, et al. [13] examined three bare hollow circular nozzle, pipe, and diffuser geometries, with no wind turbine and area ratio of 1/4, 1, and 4, respectively, and L/D = 7.7 in wind tunnel experiments as shown in Figure 5. Air flows with smoke strip visualization technique were used through inside and outside of the three model devices. Results indicated that air flows avoided the nozzle-type model instead air better flows into the diffuser-type model because air was sucked into diffuser due to the back suction side. It was also shown that wind speed gradually increased with L/D; hence, it was concluded that the diffuser structure is most effective for collecting and accelerating the wind. A remarkable increase in wind speed ratio was obtained at inlet of diffuser, between 1.6 to 2.4, if a long diffuser over L/D = 3 is used; however, it was preferable to have a shorter diffuser body with a L/D of less than 2 for their shroud wind turbine so that they examined several short diffuser-type structures with end flanges to achieve high velocity ratio at inlet.
Ohya, et al. [13] presented experimental wind velocity and static pressure distribution on the central axis of the hollow circular devices. These data will be used for validation of our simple mathematical model and also to verify our CFD computations. Below, the simple mathematical models are presented for horizontal devices. The same idea can be explored when using the devices in vertical orientation; however, it is avoided here due to lack of experimental data; instead, more reliable CFD simulation are carried out to compare if there is any appreciable difference between the accelerating devices with horizontal and vertical orientation.
Horizontal pipe flows
Here, simple mathematical models based on energy equation by some head losses are developed for external flows over pipe, nozzle, and diffuser at locations 0, 1, and 2 as shown in Figure 5.
In general, the external flows over and inside the horizontal pipe is highly complicated due to inlet and outlet interaction with free stream flow, developing inner and outer boundary layers outside and inside pipe, entrance pipe undeveloped flow, turbulent flows inside and outside pipe. To simplify this, it is assumed that the inlet effect is to raise entrance pressure so that pressure gradient along inside pipe allows for flowing air through the pipe. Hence, air velocity at inlet and through pipe will be lower than free stream velocity. By writing energy equation from point 0 to point 1, including inlet minor loss with the loss coefficient of k1 as follows [45]:
Energy equation for air flows inside pipe between point 1 and point 2 is expressed by [45]:
From continuity equation, the volume flow rates at inlet and outlet of the pipe must be equal; hence, for constant cross sectional area of the pipe, the inlet and outlet average velocities are equal; i.e. , although the kinetic energy coefficients are not equal because of different velocity profiles at inlet and outlet for this undeveloped fluid flow; i.e. α1 ≠ α2. At inlet however, the inlet velocity is assumed nearly uniform, V1c ≈ V0, for which α1 = 1, and at the outlet, the velocity profile is assumed turbulent with , in which V is the velocity at radius r and Vc is the centreline velocity. For general turbulent flows with n = 7, the average velocity in outlet is given by: , and hence by assuming similar average velocity at inlet, it yields to: ; α2 = 1.2245. From Ohya, et al. [13] experiments, the outlet pressure can be nearly approximated by the free stream pressure; i.e. P2 ≈ P0; hence, equations (1) and (2) can be simplified as:
Equating right hand sides of (3) and (4), the relation between inlet and free stream velocities are obtained as follows:
For the air velocity of V0 = 5 m/s, the Reynolds number value is Re = 4.1 × 104, hence by using Moody diagram, the friction coefficient for a smooth pipe is obtained as: f = 0.021. For a typical loss coefficient of k1 = 0.02 (from reference [45]), although the loss coefficients should be obtained from experiments, the inlet average velocity is calculated from (5) as: , and consequently the outlet centreline velocity is obtained as: V2c = 1.03 V0.
This is in good agreement with experiments as shown in Figure 6. Although for each case, the coefficients of the head losses should be determined from experiments.
In order to determine pressure coefficient, , for the inlet and outlet centreline of the pipe, equation (4) is rewritten as follow to obtain pressure coefficient:
.
For the pipe with the given values above, Cp1 = 0.237, Cp2 = 0. This slightly overestimates experiment as shown in Figure 7.
Horizontal nozzle flows
As shown in Figure 5, the external and internal flow over an open nozzle is considered here. A mathematical model is developed based on energy equation considering inlet and interior head losses. Experiments by Ohya, et al. [13] suggested that a high pressure zone created at the nozzle inlet avoided air to easily enter the nozzle and this limited mass flow rate passing through the nozzle. It was observed that air velocity at the outlet of nozzle did not increased from the value at upstream value and hence the nozzle was not considered as suitable device to accelerate air speed. The inlet velocity was also considerably reduced compared with upstream velocity. From these observations, air velocity and pressure coefficient at inlet and outlet of the nozzle can be estimated using continuity and energy equations. Writing energy equation from point 0 to point 1 for the horizontal nozzle including the nozzle inlet loss (k1) as follows [45]:
Energy equation for air flows inside the nozzle between point 1 and point 2 can be expressed by [41]:
The nozzle loss coefficient k2 for a typical nozzle may be found in reference [45]. From continuity equation, the volume flow rates at inlet and outlet of the pipe must be equal; hence, for the area ratio of 4 between inlet and outlet of the nozzle, the inlet and outlet average velocities are given by, i.e. . As observed from Ohya, et al. [13] experiments, the outlet centreline velocity is nearly equals to upstream velocity, i.e. V2c ≈ V0, for which α2 = 1 Similar to the pipe flows, the kinetic energy coefficients at inlet and outlet are different so that by assuming nearly uniform flow at inlet, we can write and . The centreline velocity values at inlet and outlet are shown in Figure 6. Similar to the pipe flows, the velocity profile is assumed turbulent with . Taking n = 7 for turbulent flows, the average velocity in outlet is given by: or and hence by assuming similar velocity profile at inlet, it yields to: .
Inserting the above findings into equation (7) and manipulating to find the inlet pressure coefficient, the following is found:
Substituting k1 = 0.02 [45] and , although the loss coefficients should be obtained from experiments, the value of pressure coefficient at inlet is found to be Cp1 = 0.94. Similarly by substituting the above given data in equation (8) and manipulating the outlet pressure coefficient is obtained as follows:
Substituting above values and k2 = 0.02 [45] in equation (10), the outlet value of pressure coefficient is obtained as Cp1 = 0.268. The pressure coefficients at inlet and outlet are shown in Figure 7 which exactly matches with experiments.
Horizontal diffuser flows
As shown in Figure 5, the external and internal flow over an open diffuser is considered here. A mathematical model is developed based on energy equation considering inlet and interior head losses. Experiments by Ohya, et al. [13] suggested that a low pressure zone developed at the diffuser inlet which accelerated air flow inside the diffuser increasing mass flow rate passing through the diffuser. It was observed that air velocity at the inlet considerably increased by a factor of 1.6 to 2.4 times of the upstream velocity. From these observations, air velocity and pressure coefficient at inlet and outlet of the diffuser can be estimated using continuity and energy equations. The same energy equations as the nozzle given in equations (7) and (8) can be used for the diffuser. Assuming the outlet pressure as atmospheric, P2= P0, and using continuity equation, , the equations (7) and (8) are combined to find outlet velocity as follows:
The loss coefficient k1 for a typical diffuser may be found in reference [45]. Taking k1 = 0.4, k2 = 0.02, A2/A1 = 4 although the loss coefficients should be obtained from experiments, the average outlet velocity is determined as: . It is also assumed that the kinetic energy coefficients are equal for this fully turbulent flow; i.e. α1 = α2 = 1. Hence with n = 7 at inlet, or V2c = 0.45V0 which greatly underestimates the outlet velocity compared with experiments. This may be due to highly viscous effects with separation of boundary layer at outlet. For the inlet velocity: or V2c = 1.8 V0 which perfectly match with experiment (Figure 6).
Inserting the above findings into equation (7) and manipulating to find the inlet pressure coefficient, the following is found:
Substituting the above values, the inlet pressure coefficient is determined as Cp1 = -2.02. The pressure coefficients at inlet and outlet are shown in Figure 7 which nearly matches with experiments.
CFD Simulations
In order to develop the vertical enclosure wind turbine, the components such as pipe, nozzle, diffuser, and Venturi should be studied when oriented in vertical direction. From the mathematical models developed in section 2, it may be discovered that the potential heads due to elevation between inlet and outlet play an important role. However, it is difficult to test such devices in vertical arrangement because most of widely used wind tunnels are designed to test objects with horizontal wind. Hence, the objective of this section is to evaluate performance of such devices in vertical wind using Computational Fluid Dynamics (CFD) simulations.
In this work, CFD simulations are performed for solving air flows over the Ohya's nozzle and diffuser outlined in section 2. The purpose is to verify and validate CFD solutions with the available wind tunnel test data [13]. The commercial CFD software, Fluent package [46], is used in this study to solve the Reynolds average Navier-Stokes (RANS) equations with (k-ω)-SST turbulence model for the three dimensional Ohya's nozzle/diffuser model. The computational domain consists of unstructured mesh with 452,000 mesh elements. The mesh inside the nozzle/diffuser arrangement was constructed using hexagonal elements as shown by Figure 6. Outside the nozzle/diffuser arrangement, the hybrid mesh element was used. The boundary conditions utilised in the current study are depicted in Figure 6. The solution is deemed converged if the difference between two consecutive iteration was less the 10-4 for all involved parameters (velocities, k,ω). The Semi Implicit Method for Pressure Linked Equation (SIMPLE) algorithm was employed for the calculation of pressure and velocity fields. Third order MUSCAL discretization scheme was used with momentum, turbulent kinetic energy, and specific dissipation and energy equations. However, the second order upwind discretization scheme was used with the pressure mode. Furthermore, the values of Y+ at the walls of nozzle/diffuser ranged from 20-85.
The CFD results for the centreline velocity and the pressure coefficient distribution are shown in Figure 7 and Figure 8, respectively. The velocity distribution results from CFD have nicely matched up with the experiments for the nozzle flow as observed in Figure 7. For the diffuser model, the CFD results agrees very well half way through the diffuser with the wind tunnel test data; but, it fails considerably the reminder of diffuser and downstream of flow because of strong viscous interaction and possible separation zone with vortex formation in the diffuser and its downstream. It appeared that the CFD results and our simple analytical model agree well for both inlet and outlet of diffuser flow. Therefore, the simple external flow over diffuser may cast an interesting example for CFD model validations to address some physical phenomena underneath flow features of such typical devices. From Figure 8 as expected, the pressure coefficient has exactly matched up with experimental data for both nozzle and diffuser flows. This indicates that pressure field has perfectly obtained using CFD simulation. However, the mismatch in velocity field should be addressed to the flow viscosity and shear stresses obtained from the studied turbulence model. This can be separately investigated and is out of scope of present study.
For the purpose of present study, two devices including circular nozzle and diffuser in vertical arrangement are examined using FLUENT software [29]. The nozzle and diffuser used here are with the Dimensions of: Length of L = 0.85 m, smaller diameter of D = 0.25 mso L/D = 3.4, and the area ratio of A2/A1 = 6. The different geometries are adopted here for a practical application for which shorter lengths of the devices are required.
External flows over nozzle
Here, CFD simulations around the vertical nozzle in external flows are presented. As shown in Figure 9, computational results for the nozzle suggest that there is no appreciable differences between lateral (horizontal) or vertical direction of wind. The interesting finding from the results in Figure 9 is that the nozzle perform as discussed in previous section by retarding flow and hence increasing pressure at inlet and then regain almost the same upstream velocity at the outlet. This clearly shows that there is fundamental difference between internal nozzle flows which accelerate upstream velocity by the nozzle area ratio. However for the open nozzle flows with internal and external flows, the external flows dictate that the velocity retard at inlet and then regain to the external upstream velocity value.
Changing the upstream air velocity from 1 m/s to 5 m/s, the effects on the centreline velocity and the pressure coefficient are shown in Figure 10 and Figure 11; respectively, for the vertical nozzle. The nozzle inlet is located at X/L = 0 and its outlet at X/L = 1. From Figure 10, it is observed that the nozzle outlet velocity has slightly increased from the upstream wind velocity by increasing wind speeds from 1 m/s to 5 m/s. This is in agreement with what was observed in experimental works in wind tunnels. However, the most interesting observation here is the pressure coefficient as shown in Figure 11. By increasing wind velocity from 1 m/s to 5 m/s, both inlet and outlet pressure coefficient increase considerably which may suggest that air avoids entering the nozzle due to formation of a high pressure zone at inlet. From CFD simulations, it can be seen that by increasing wind velocity the accelerated zone forms at exterior part of inlet causing less air mass flow rate to pass through the interior part of nozzle. Moreover, high pressure zones forms at inlet and outlet of nozzle pushing more air to pass from exterior part of nozzle due to low pressure there. The general structure of pressure contours around the nozzle remains unchanged except the high pressure values magnify by increasing wind speed (Figure 11).
External flows over diffuse
CFD simulations around the vertical diffuser are investigated here in external flows. The objective is to examine by changing the upstream air velocity from 1 m/s to 5 m/s what will be the effects on the centreline velocity and the pressure coefficient. Similar to the nozzle problem, the diffuser inlet is located at X/L = 0 and its outlet at X/L = 1. The centreline velocity and pressure coefficient are shown in Figure 12 and Figure 13, respectively. From Figure 12, it is observed that inlet velocity of diffuser increases by a factor of 1.2 to 1.3, for this particular design, by changing wind velocity from 1 m/s to 5 m/s. However unlike Ohya's diffuser, the outlet velocity of the diffuser has not recovered to the free stream velocity. The strong suction at outlet also caused a reverse flow region just downstream of diffuser shown in Figure 12 by negative velocity zone from X/L = 1.26 to X = 1.84. Considering the pressure coefficient as shown in Figure 13, there is considerable decrease of pressure at inlet causes air sucked into the interior of the diffuser. This is interestingly in agreement with experiments of Ohya, et al. [13], although there is vacuum at outlet of diffuser too which increases by increasing wind speed.
Conclusions
In this study, the review of accelerating devices in wind power generation was given. From several studies in wind turbines with shroud diffuser, it is observed that it may be more practical to use diffuser assisted wind collectors. The concept was also proved practical in the literature of wind catchers widely used in architecture of buildings. In this study the following are found:
1. Some of literature suggests that the bare accelerator devices are responsible for wind velocity and wind power augmentation. But, other part of literature considers the interaction between a wind turbine and an accelerator device such as diffuser is the cause for flow augmentation.
2. To clear these points and also to have better understanding of air flows around accelerator devices, some simple mathematical models introduced which compares well with the available experimental data in cases of pipe and nozzle flows; however, there is a mismatch between diffuser outlet data with experiments perhaps due to high viscous flow interaction there.
3. There is not much known on performance of accelerating devices when are used in vertical enclosure wind turbines. To examine the function of different accelerating devices such as nozzles and diffusers in vertical orientation, CFD simulation were performed which indicated that there is no appreciable differences of using these devices in horizontal or vertical arrangements.
4. CFD solutions over nozzle flows shows high pressure augmentation at inlet which may prohibit air for entry to the nozzle and so reduces mass flow rate. The device may be utilized after air collection by a diffuser to accelerate wind speed to desirable speed for operation of wind turbine.
5. CFD simulations of diffuser devices also confirmed the generation of a suction zone which improves considerably intake of air into the diffuser.
6. From these observations, it is understand that to collect and accelerate wind in enclosure wind turbines, the design of each accelerating devices should be considered separately for the full range of operational wind speeds and carefully design the full structure of enclosure wind turbine to operate optimally for practical range of wind speeds.
7. Considering conventional wind turbines, the range of wind speed is within 3 m/s to 25 m/s. But, new innovative designs may extend this operational range of wind speeds through which the power generation may also aligned with wider range. From practical point of view, it is required that some electrical generators to operate at very wide range of powers or alternatively the control devices may be needed to avoid overload of such electric generators.