International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5106/4125
A New Non-Time Based Tracking Control for Mobile Robot
Xiao-Feng Liu, Ren-Fang Zhou and Guo-Ping Cai*
Table of Content
Figures

Figure 5: Tracking a circle curve with different....
Tracking a circle curve with different initial error (Reference Point is Pr1).
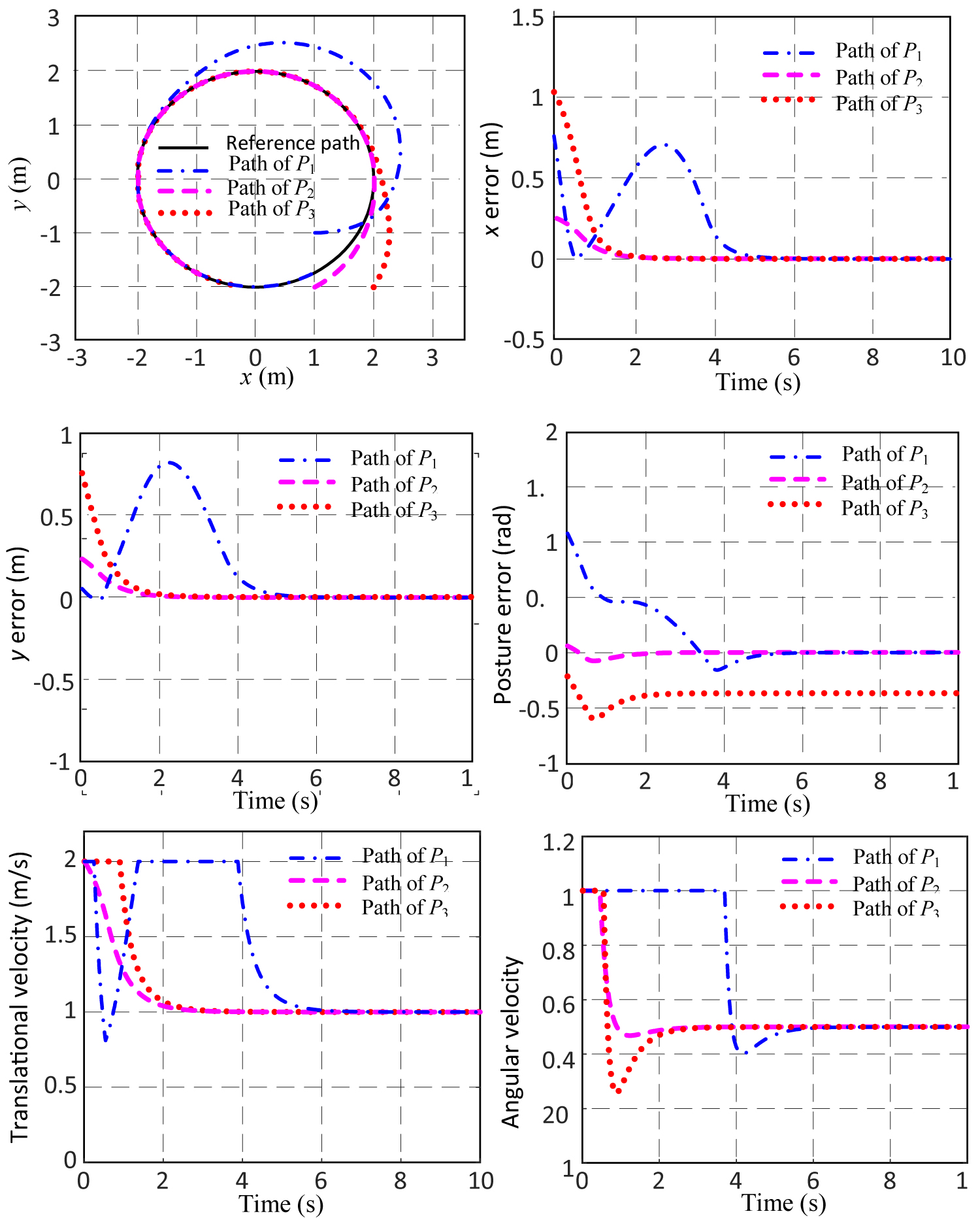
Figure 6: Tracking a circle curve with different...
Tracking a circle curve with different initial error (Reference Point is Pr2).
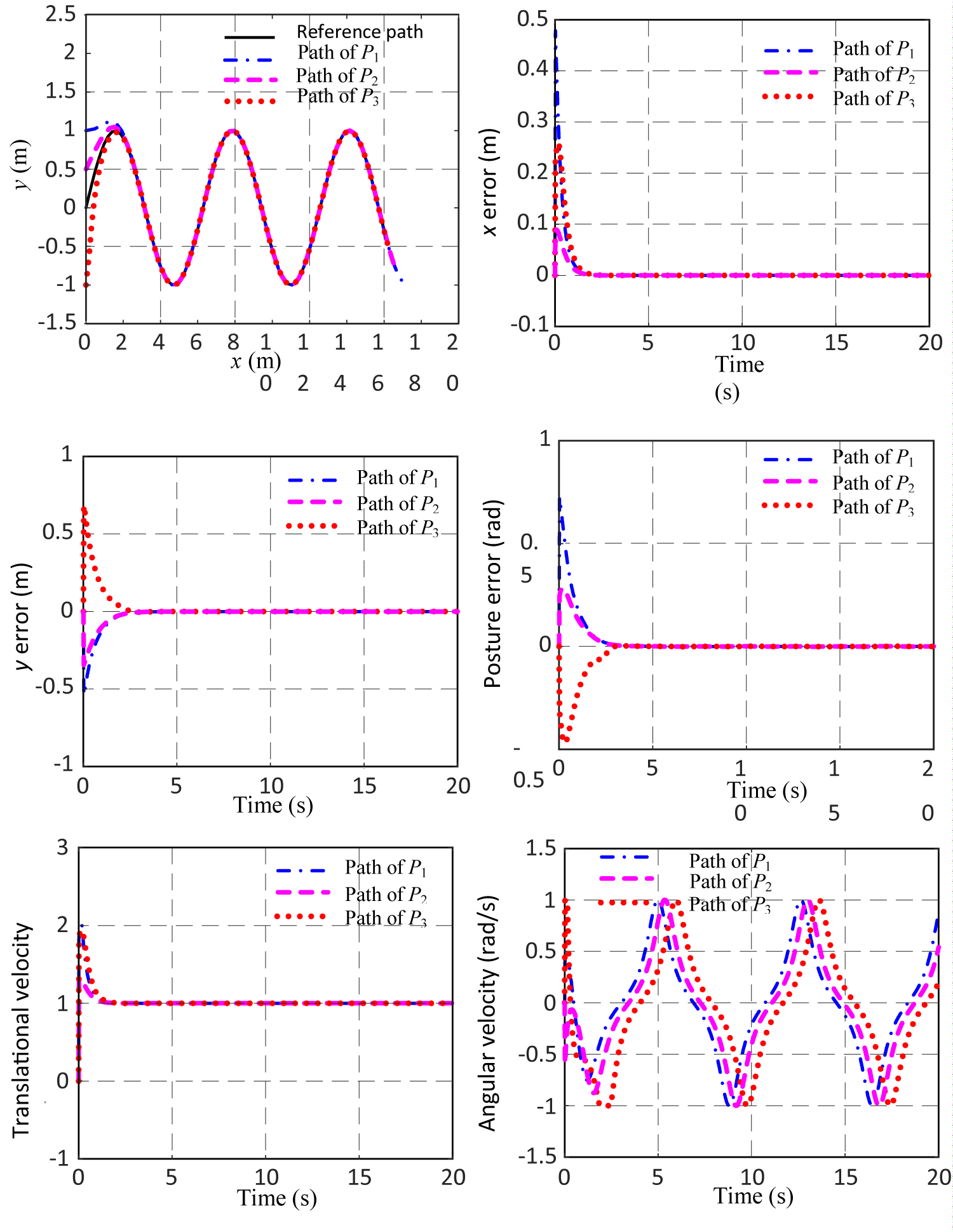
Figure 7: Tracking a sine curve with different initial...
Tracking a sine curve with different initial error (Reference Point is Pr1).
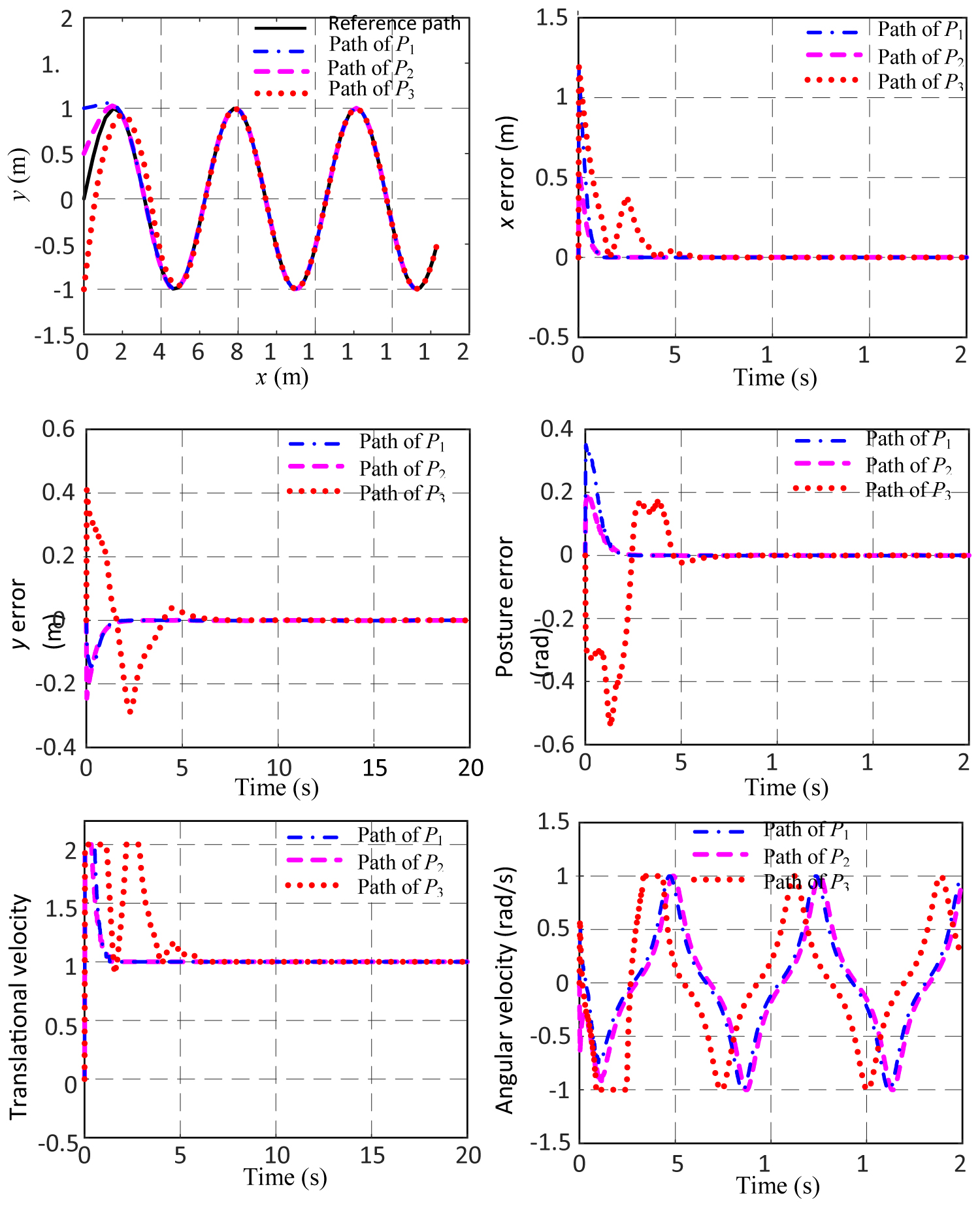
Figure 8: Tracking a sine curve with different.....
Tracking a sine curve with different initial error (Reference Point is Pr2).
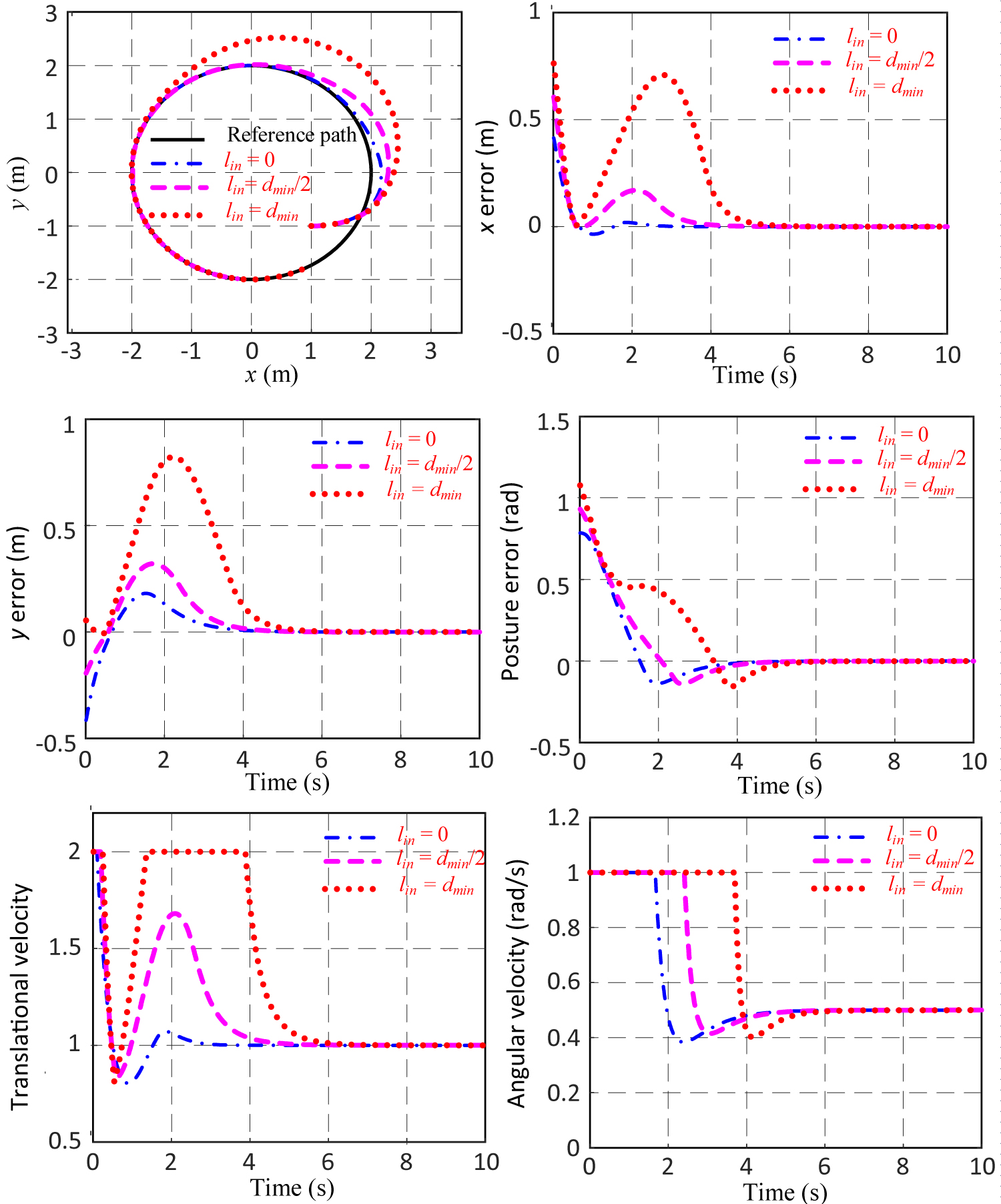
Figure 9: Tracking a circle curve with the same....
Tracking a circle curve with the same initial error, with different lin.
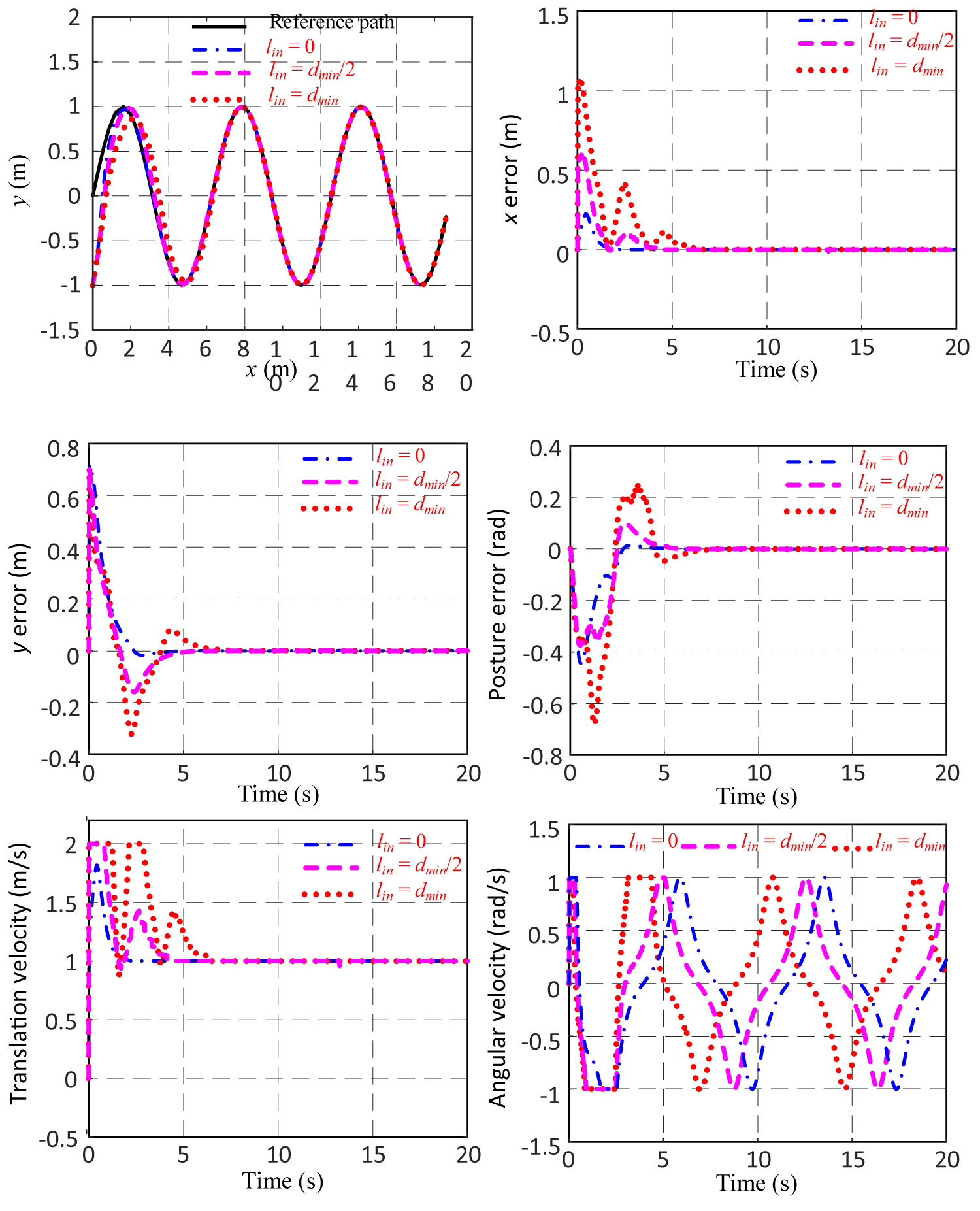
Figure 10: Tracking a sine curve with the same initial.....
Tracking a sine curve with the same initial error, with different lin.

Figure 11: Tracking control with dynamic obstacle: a) Position.....
Tracking control with dynamic obstacle: a) Position of the robot; b) Velocity of the robot.
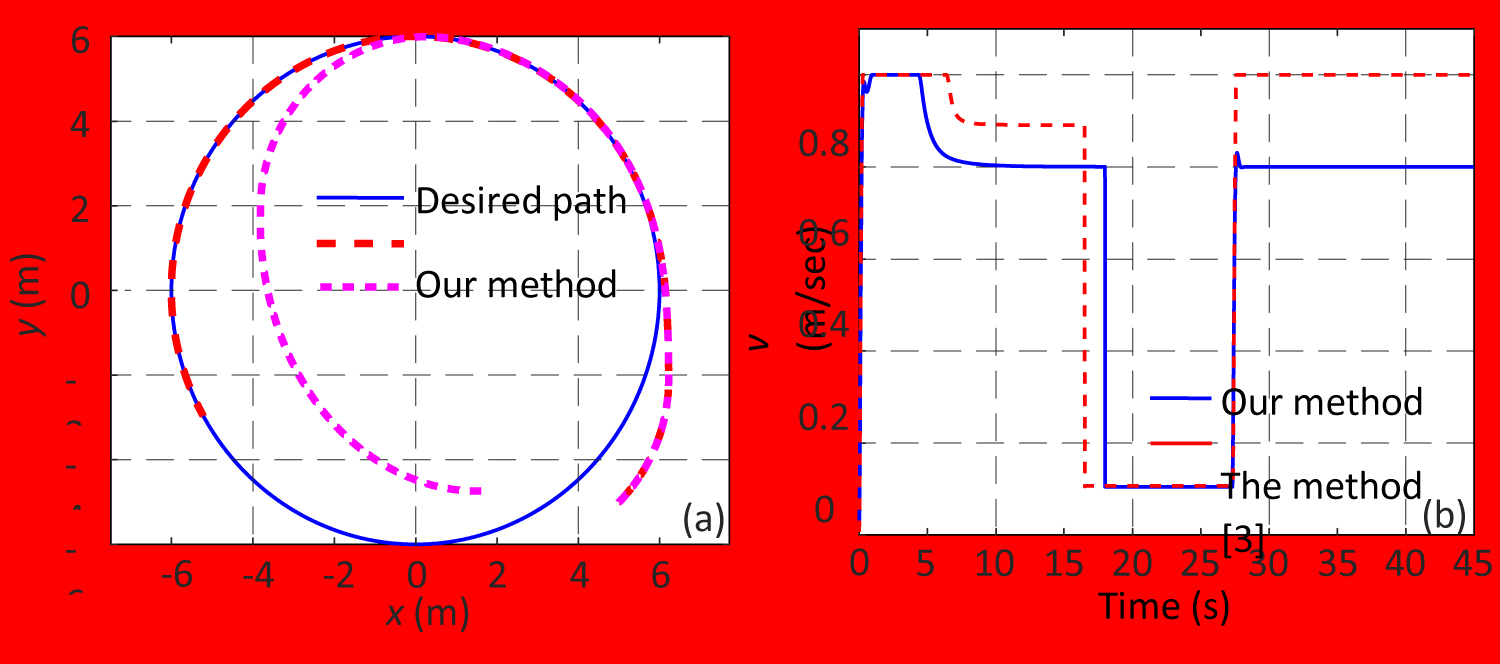
Figure 12: Tracking control with tire skidding.....
Tracking control with tire skidding: a) Position of the robot; b) Velocity of the robot.
References
- Park BS, Yoo SJ, Jin BP, Choi YH (2010) A simple adaptive control approach for trajectory tracking of electrically driven nonholonomic mobile robots. IEEE Transactions on Control Systems Technology 18: 1199-1206.
- Oriolo G, Luca AD, Vendittelli M (2002) WMR control via dynamic feedback linearization: Design, implementation, and experimental validation. IEEE Transactions on Control Systems Technology 10: 835-852.
- Khooban MH (2014) Design an intelligent proportional-derivative PD feedback linearization control for nonholonomic-wheeled mobile robot. Journal of Intelligent and Fuzzy Systems 26: 1833-1843.
- Kanayama Y, Kimura Y, Miyazaki F, Noguchi T (1990) A stable tracking control method for an autonomous mobile robot. IEEE International Conference on Robotics and Automation, Cincinnati, USA, 384-389.
- Wang Z, Li SH, Fei SH (2009) Finite-time tracking control of a nonholonomic mobile robot. Asian Journal of Control 11: 344-357.
- Ou MY, Li SH, Wang CL (2014) Finite-time tracking control for nonholonomic mobile robots based on visual servoing. Asian Journal of Control 16: 679-691.
- Ollero A, Amidi O (1991) Predictive path tracking of mobile robots. Application to the CMU NavLab. IEEE International Conference on Advanced Robotics, Pisa, Italy, 1081-1086.
- Velasco-Villa M, Del-Muro-Cuellar B, Alvarez-Aguirre A (2007) Smith-predictor compensator for a delayed omnidirectional mobile robot. Control and Automation, Athens, Greece, 1-6.
- Kecskés I, Odry P (2012) Fuzzy route control of dynamic model of four wheeled mobile robot. IEEE International Symposium on Logistics and Industrial Informatics, Smolenice, Slovakia, 437-440.
- García-Cerezo A, Ollero A, Martínez JL (1995) Design of a robust high-performance fuzzy path tracker for autonomous vehicles. International Journal of Systems Science 27: 799-806.
- Matraji I, Al-Durra A, Haryono A, Al-Wahedi K, Abou-Khousa M (2018) Trajectory tracking control of skid-steered mobile robot based on adaptive second order sliding mode control. Control Engineering Practice 72: 167-176.
- Carlucho I, Paula MD, Acosta GG (2019) Double Q-PID algorithm for mobile robot control. Expert Systems with Applications 137: 292-307.
- Ren C, Li X, Yang X, Ma S (2019) Extended state observer-based sliding mode control of an omnidirectional mobile robot with friction compensation. IEEE Transactions on Industrial Electronics 66: 9480-9489.
- Wei K, Ning X, Tan JD (1999) Analysis and design of non-time based motion controller for mobile robots. IEEE International Conference on Robotics and Automation, Detroit, USA, 4: 2964-2969.
- Wang DY, Ma XD, Dai XZ (2004) Non-time based path tracking control for mobile robots. Robot 26: 198-203.
- Coulter RC (1992) Implementation of the pure pursuit path tracking algorithm. Technical Report CMU-RI-TR-92-01, Robotics Institute, Carnegie Mellon University, ?Allegheny.
- Snider JM (2009) Automatic steering methods for autonomous automobile path tracking. Technical Report CMU-RI-TR-09-08, Robotics Institute, Carnegie Mellon University, Allegheny.
- Morales J, Martínez JL, Martínez MA, Mandow A (2009) Pure-pursuit reactive path tracking for nonholonomic mobile robots with a 2D laser scanner. Eurasip Journal on Advances in Signal Processing 2009: 1-10.
- Yamasaki T, Takano H, Baba Y (2009) Robust path-following for UAV using pure pursuit guidance. Aerial Vehicles, 671-690.
- Elbanhawi M, Simic M, Jazar R (2017) Receding horizon lateral vehicle control for pure pursuit path tracking. Journal of Vibration and Control 24: 3.
- Ohta H, Akai N, Takeuchi E, Kato S, Edahiro M (2016) Pure pursuit revisited: field testing of autonomous vehicles in urban areas. IEEE International Conference on Cyber-Physical Systems, Networks, and Applications, 7-12.
- Elbanhawi M, Simic M, Jazar R (2016) The effect of receding horizon pure pursuit control on passenger comfort in autonomous vehicles. Intelligent Interactive Multimedia Systems and Services, Springer, Germany.
Author Details
Xiao-Feng Liu, Ren-Fang Zhou and Guo-Ping Cai*
School of Naval Architecture, Ocean & Civil Engineering, State Key Laboratory of Ocean Engineering, Key Laboratory of Hydrodynamics of Ministry of Education, Shanghai Jiaotong University, China
Corresponding author
Guo-Ping Cai, School of Naval Architecture, Ocean & Civil Engineering, State Key Laboratory of Ocean Engineering, Key Laboratory of Hydrodynamics of Ministry of Education, Shanghai Jiaotong University, Shanghai 200240, China.
Accepted: June 15, 2020 | Published Online: June 17, 2020
Citation: Xiao-Feng L, Ren-Fang Z, Guo-Ping C (2020) A New Non-Time Based Tracking Control for Mobile Robot. Int J Robot Eng 5:025.
Copyright: © 2020 Xiao-Feng L, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This paper proposed a new trajectory tracking control method based on non-time motion reference for non-holonomic mobile robots. Different from the traditional time-based control theory, this method determines the reference points through the geometrical relationship between the current position and the desired path. Substituting them into the time based motion controller, a non-time based motion controller can be derived. Since the reference points are only related to the current state of the robot, the method proposed gets rid of the influence by time, thereby avoiding the disadvantages of loss of tracking ability when the mobile robot encounters undesired incidents such as motor shutdown or tire skids. Finally, the feasibility of this method is verified through numerical simulations of typical path tracking.
Keywords
Mobile robot, Non-time based motion controller, Reference point, Trajectory tracking
Introduction
A wheeled mobile robot is one kind of typical system with non-holonomic constraints [1], and has been paid much attention because of the difficulties and challenges on its path tracking control issue. Solving it, many scholars consider desired paths as functions with respect to time, and study on the path tracking control problem in time-domain. Dynamic state feedback linearization method [2,3] and non-linear control method based on Lyapunov [4-6] are the two classical control methods. The tracking problems of them are solved in time-domain, therefore the resulting tracking errors and control laws are time-dependent. Facing the situation of tire skids, obstacles or motor shutdown, it may occur that the tracking errors of the mobile robot abruptly change or increase with time under the control of these methods. This may degrade the tracking effect of the mobile robot, and moreover lead to the loss of the ability to track the ideal path in some extreme circumstances.
What causes the problem above is that the determination of the reference point is only related to time but not to the current states of the robot, which leads to the incompatibility of motion planning and actual control. To overcome the shortcomings of the above means, predictive control methods [7,8] and fuzzy control [9,10] methods and others [11-13] have been carried out. In these methods, although different ways are proposed to deal with the tire skids, obstacles or motor shutdown, they still use the time as the variable to design the controller. Thus, they still some disadvantages, such as slow reaction time or too complex controller structure. Different from the above method, Wei [14] proposed a non-time based controller designed by the reference variables of time-independent state variables, such as arc length or projection of the coordinate axes of the current position, and used STR (state to reference) mapping to convert time reference controller to non-time based controller. The article points out that the stability of a non-time based controller is determined by the stability of time reference controller, and the relevant proof is derived. Overcoming the shortcomings of time reference control law to some extent, this method is still complicated to be realized, and the STR mapping is hard to find. Similar to the design concept of Wei’s controller, Wang [15] considered the x-axis projection of the position of the robot as the reference variable, and designed a path tracking controller according to Lyapunov stability method. Although the effectiveness was verified by simulations, this control method existed the problem of singularity and in-continuity. The main reasons for the existing problems of the two methods mentioned above are that the non-time reference variables selected in the controller design process do not own the characteristic of monotone increment and that the curve is a one-one mapping of a reference variable, which reference time t has. In another word, it is difficult to find a non-time reference variable having all the advantages that time reference variable t has.
Since there is not a perfect non-time reference variable for controller design, then is there another way to design the non-time reference controller? In 1992, Coulter [16] applied the pure pursuit algorithm into the research of the path tracking method of the mobile robot and discussed the implementation of it, which is a non-time reference control method. Snider made a comparative study on the pure pursuit, Stanley method, error-based kinematics trackers and linear quadratic dynamic controllers in 2009, and showed that pure pursuit had a better performance than other controllers under conditions of random excitation and discontinuous paths. The concept of pure pursuit was widely used in the studies of path tracking control problems afterward [17-22], and received the good achievement. However, there are still some deficiencies in the pure pursuit method. Pure pursuit method searches for the target point through a constant lookahead distance, which will lead to the problems such as unable to find the target point, or to track the large curvature path with high precision. Moreover, as a lateral control method, the pure pursuit controller cannot adjust the longitudinal velocity, which limits the control effectiveness.
From the explanation above, it can be seen that there are still some insufficiencies in the two major non-time reference control methods, but core ideas of these two methods still make sense of the study on non-time reference control. Based on the two non-time reference algorithms mentioned above, this paper carried out a new non-time reference path tracking control method. Different from the means to obtain non-time reference point through STR mapping introduced by Wei [14], this paper draws on the advantage of the pure pursuit method [16], as well as uses geometric means to obtain control reference points and tracking control errors, and finally substitute them into time reference controller to realize the conversion to non-time reference controller. Simulations of several typical routes are carried out, and the results of which verifies the effectiveness of the method of this paper.
This paper is organized as follows: Section 4 introduces the model of differential drive wheeled robot; the design process of the controller is presented in Section 5; in Section 6, simulations on path tracking of circles and sinusoid are carried out to verify the effectiveness and feasibility of the method introduced in this paper; and Section 7 shows the conclusions of this paper.
Model of Mobile Robot System
The research object of this paper is a differential wheeled mobile robot, and structural model of which are depicted in Figure 1. In Figure 1, C is the central point of the axis of the two driving wheels, namely the central point of the robot, and d is the distance between the two driving wheels. The kinematic equation of the central point of the robot can be expressed as
Where (x, y) is the location of the central point in the inertial coordinate system, is the attitude angle of the mobile robot relative to x-axis, v and ω are the translational velocity and the angular velocity of the mobile robot respectively.
Supposing that there are no tire skids in the motion process, the movement of the mobile robot satisfies
Design of the Controller
From the work done by Wei [14] and Wang [15], it can be inferred that whether by STR conversion or by direct derivation, a path tracking controller of a non-time based reference variable can be obtained for the mobile robot. However, hard to find a non-time based variable having the characteristics of monotone increasing and unicity which reference time t has, there are problems such as decrease of the non-time based variable with the increase of curve length, a one-to-many mapping between non-time base variable and trajectory reference point, and not found of the reference point when controlling with non-time based variable. Different from the method above, the pure pursuit control method designs the controller through geometric means. This method firstly finds out the target point on the tracking trajectory by a constant lookahead distance, and then uses the target point to derive a circular arc passing the current robot position and the target point, and finally solve control output by the radius of the arc. Though this pure geometric control method overcomes the disadvantages of the non-time based variable radically, it brings some new problems, such as the control oscillation that appears when there is a sudden change in the curvature of the tracking curve, which is caused by the neglect of the position relationship between the current robot position and the tracking trajectory. In addition, the pure pursuit is actually a lateral control method, and cannot adjust the longitudinal velocity of the mobile, which lower the effectiveness of the controller to some extent.
A new non-time based control method is proposed in this paper, combining the merits of the two methods above. In this method, it is prior to design a time based controller, then geometric means are taken to obtain the trajectory reference point and calculate the tracking error, and finally a non-time based controller can be derived by replacing the tracking error based time with the geometric tracking error. The detail design process of the controller is described as follows.
Time based controller
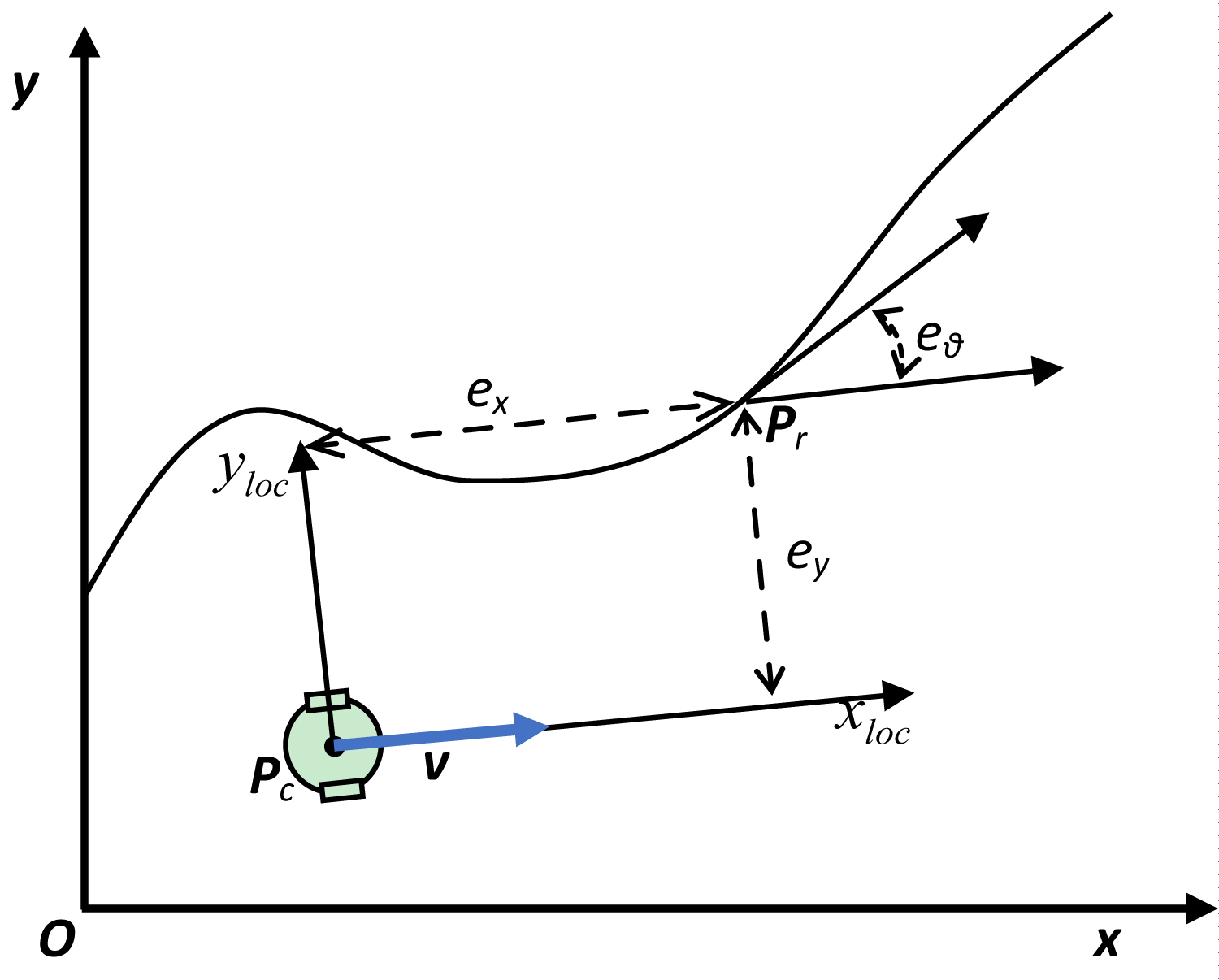
As shown in Figure 2, in current time, the reference attitude of the mobile robot on the desired trajectory is defined as , the reference velocity is , and the current position of the robot is . In the inertial coordinate system, the attitude error of the robot is
The projection of the attitude error on the robot body-fixed is [4]
Derived with respect to time, the above equation can be derived into [3]
Where, and are the reference translational velocity and reference angular velocity respectively. According to Lyapunov stability method, the controller of the mobile robot can be obtained as [3]
Consider the limitation of maximum translational velocity and maximum angular velocity of the actual robot motion, the amplitude of the controller can be limited as
Selection of the reference point
The process to search for a control target point through a geometric relationship is given in the following. As could be seen in Figure 2, the desired path equation is y = f (x), Pc = [xc, yc, θc]T is the current configuration of the vehicle, square of the distance from Pc to an arbitrary point Pa = [x, y, θ]T on the desired path could be calculated as L2 (x) = (xc - x)2 + (yc - y)2. Let the minimum distance between Pc and Pa is dmin. At this situation, Pa is called the target point and denoted by Pr1. Since Pr1 is the closest point to Pc, xr1 is an extreme point of L2 (x), and Pr1 meets
By solving the above equation, we can get the values of xr1 and yr1.
In the method discussed in this paper, besides Pr1 is selected as a reference point of non-time based motion control, the ending point Pr2 of the intercept segment from Pr1 along the forward direction of the reference trajectory with the intercept length linis also selected as a reference point of non-time based motion control. The intercept length lincan take on any value, which is like as the lookahead distance in the pure pursuit method [13]. When lin= 0, Pr2 = Pr1. The calculation process of the circular trajectories and arbitrary trajectories are given as follow.
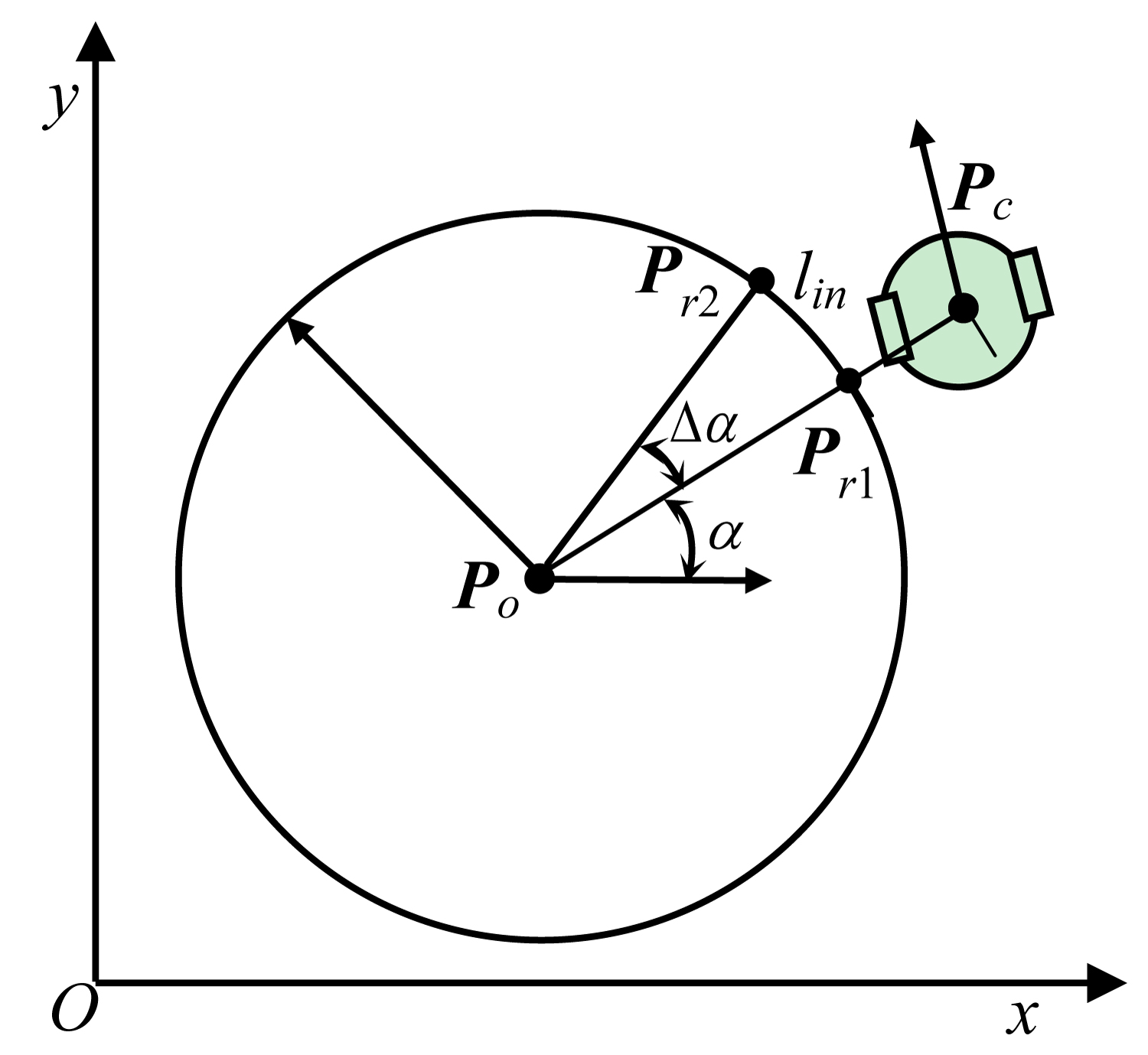
Circular trajectories tracking
As shown in Figure 3, let the equation of the circular trajectory to be tracked is . Point Po(xo, yo), the center of the circular trajectory, and the current position of the mobile robot is Pc = [xc, yc, θc]T. The closest point Pr1 from the point Pc to the circular trajectory is the cross point of that trajectory and the line segment PoPc. Let the angle between the positive direction of x axis and the line segment PoPc is α, and the position and attitude of reference point Pr1 can be expressed as
The reference point Pr2 can be found along the circular trajectory with the intercept length lin, and let the angle opposite to the arc between Pr2 and Pr1 to be ,with
And the position and attitude of reference point Pr2 is
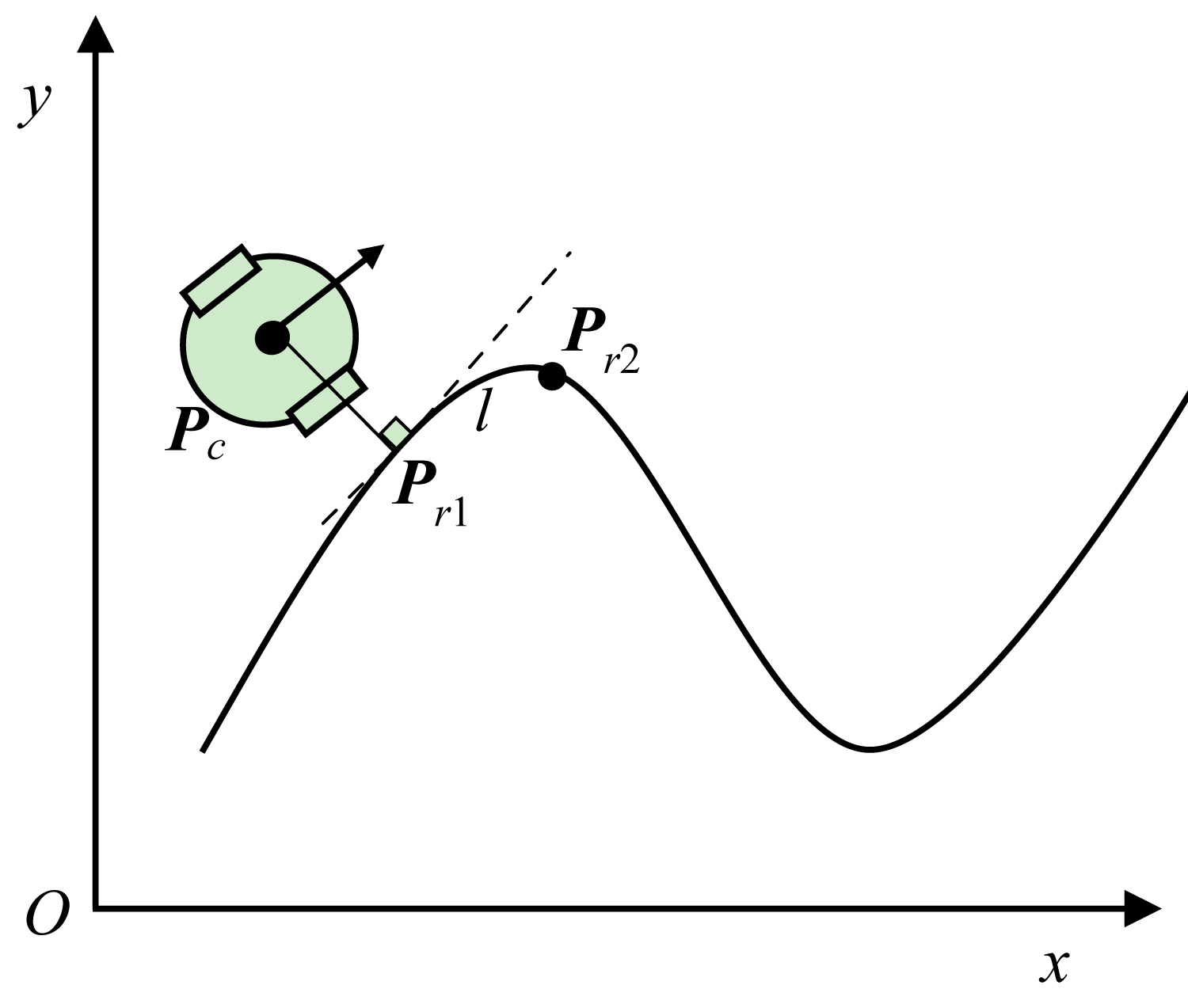
Arbitrary trajectories tracking
As could be seen in Figure 4, let the trajectory function of an arbitrary continuous curve to be y = f (x), and according to equation (8), the reference point Pr1 satisfies the equation as
The equation above is commonly nonlinear, and the least square iteration method is used to solve it. The coordinates corresponding to Pr1 is
It is not guaranteed that an arbitrary continuous curve must be an elementary integrable curve, so the coordinates of Pr2 cannot be calculated from the intercept length linof the curve by analytic calculation. Numerical integration method is used in this paper to obtain the coordinates of Pr2.
Numerical Simulation
To verify the effectiveness of the control method proposed in this paper, numerical simulations of the circles and sinusoids trajectory tracking of the mobile robot are carried out in MATLAB.
In the simulations of circular trajectory, the trajectory equation is x2 + y2 = 16, and the mobile robot starts from three different initial positions, P1 = [1, -1, 0]T, P2 = [1, -2, π/6]T and P3 = [2, -2, π/3]T, to track the circular trajectory under control. In the simulations of sine curve tracking, the trajectory equation of the tracked sinusoids is y = sin(x + π/2), the mobile robot is also started from the three initial positions that are P1 = [0, -1, 0]T, P2 = [0, 0.5, π/6]T and P3 = [0, -1, π/3]T. In the above simulations, the desired translational velocity of the robot is vr = 1 m/s, the maximum translational velocity is vmax = 2 m/s, the maximum angular velocity is ωmax = 1 rad/s, and the control parameters are Kx = 4, Ky = 5, Kθ = 5. The result of the simulations is depicted in Figure 5, Figure 6, Figure 7 and Figure 8. It can be seen from the simulation results that the control method proposed in this paper could achieve a good effect on all the two kinds of trajectories. Compared the calculating results of the two kinds of reference points, it can be seen that the first kind of reference points Pr1 enables the mobile robot track on the target curves faster, and the tracking process is more smooth.
If the length of forward direction interception linis considered as a variable, the reference point Pr1 can be regarded as on extreme condition when lin= 0. Selecting 0, dmin/2 and dmin as the intercept length lin, and substituting the obtained reference points into the tracking control simulations of trajectories of circle curve and sine curve, the results are shown in Figure 9 and Figure 10. The simulation results show that forward direction interception length of reference trajectories have an evident influence on the control effects. The time and distance taken to track the desired trajectory and the smoothness of the trajectory passed by the mobile robot are all inversely proportional to the length of forward direction interception, and the control output is proportional to the length. This means that the length of forward direction interception can be considered as a control parameter, and we can adjust the length according to the different demands to achieve the control goals.
From the above results, it can be got that the proposed method is effective when the environment is ideal. Next, two simulations will be performed to demonstrate the effectiveness of the proposal for dynamic obstacle and tire skidding, in which the robot will be controlled to track a circle. The control parameters is the same as the above simulations. The results are plotted in Figure 11 and Figure 12. Observing Figure 11b, it can be found that during 15s-20s, the robot velocity is 0, which means the robot encounters a dynamic obstacle that goes away at 20 s. As can be seen from Figure 11a, it can be got that the robot controlled by the proposed method can track the desired path, but the time-based method in [3] can not. Observing Figure 12b, t can be found that during 13s-27s, the robot velocity is smaller than 0.2, which means the robot encounters tire skidding. As can be seen from Figure 12a, it can be got that the robot controlled by the proposed method can track the desired path after tire skidding goes away, but the time-based method in [3] can not. These results demonstrate that the proposed method is effective for dealing with the dynamic obstacle and the tire skidding, which is the advantage of the proposal.
Conclusion
For overcoming the shortcomings of the time based trajectory tracking control methods, this paper proposed a control method based on non-time based motion control concept. This method uses geometric criteria to select reference point, avoiding the disadvantages of time based controllers very well, as well as the insufficiency of the controllers designed by non-time based reference variables. In this method, the tracking control is only related to the actual condition of the robot, not to time. As a result, it is more general and applicable. Numerical simulations not only verify the effectiveness of the method, but also indicate that the forward direction interception length can be considered as the adjustable parameter of the controller, and the control effects can be adjusted by varying the length. Though the good effectiveness of the method to track simple curves as well as complex curves has been proved by the simulations, it is still a pity that we have not carry out the proof of the effectiveness of the controller through theoretical derivation. We are hoping to research more deeply on the method through theoretical means to give out the theoretical proof of the effectiveness of it.
Acknowledgement
This work was supported by the Natural Science Foundation of China [grant number 11772187 and 11802174], the China Postdoctoral Science Foundation [grant number 2018M632104].