
International Journal of Nanoparticles and Nanotechnology
(ISSN: 2631-5084)
Volume 6, Issue 1
Research Article
DOI: 10.35840/2631-5084/5535
Spin-Waves Excitations in Segmented Nanotubes Consisting of Ferromagnetic and Non-Magnetic Materials
VA Tanriverdiyev*
Table of Content
Figures
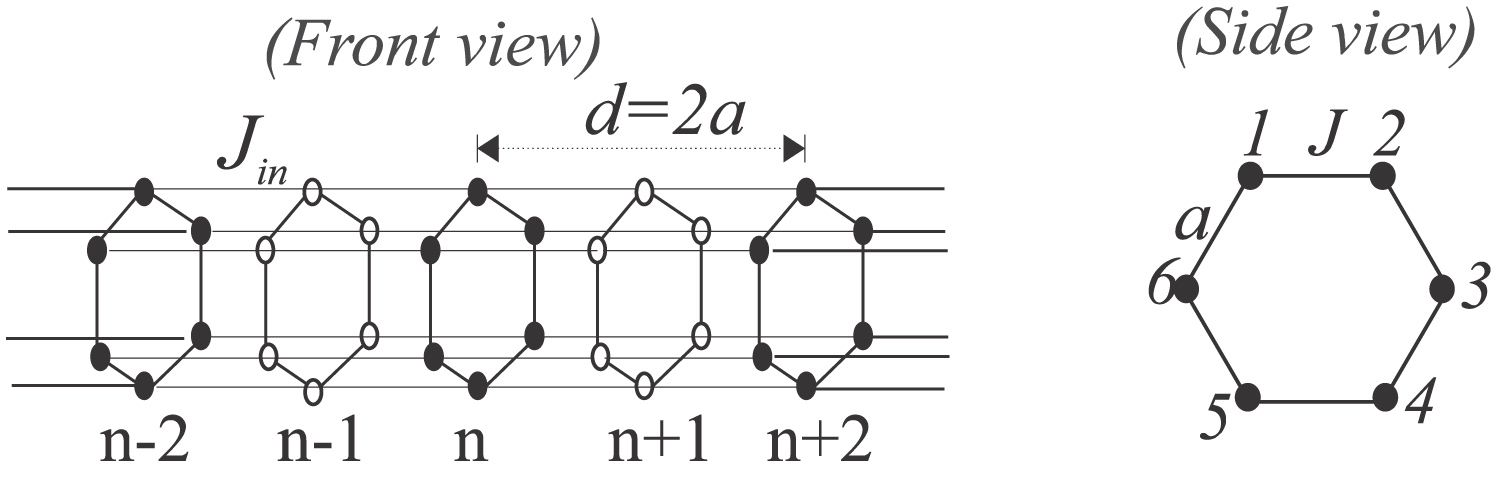
Figure 1: The schematic representation of hexagonal segmented....
The schematic representation of hexagonal segmented nanotubes. The black and white spheres indicate atoms of ferromagnetic and non-magnetic materials, respectively.

Figure 2: Spin-waves dispersion curves for propagation along...
Spin-waves dispersion curves for propagation along the HSNT with parameters , , .

Figure 3: The temperature dependence of magnetization in...
The temperature dependence of magnetization in the HSNT. The parameters are , , .
References
- S Castillo-Sepulveda, RM Corona, D Altbir, J Escrig (2016) Magnetic properties of mosaic nanocomposites composed of nickel and cobalt nanowires. Journal of Magnetism and Magnetic Materials 416: 325-328.
- D Neumaier, D Vogl, J Eroms, D Weiss (2008) Quantum transport in ferromagnetic Permalloy nanostructures. Phys Rev B 78: 174424.
- N Gao, HJ Wang, EH Yang (2010) An experimental study on ferromagnetic nickel nanowires functionalized with antibodies for cell separation. Nanotechnology 21: 105107.
- YP Ivanov, A Chuvilin, S Lopatin, J Kosel (2016) Modulated magnetic nanowires for controlling domain wall motion: toward 3D magnetic memories. ACS Nano 10: 5326-5332.
- AJ Grutter, KL Krycka, EV Tartakovskaya, JA Borchers, KSM Reddy, et al. (2017) Complex three-dimensional magnetic ordering in segmented nanowire arrays. ACS Nano 11: 8311-8319.
- TS Ramulu, R Venu, B Sinha, SS Yoon, CG Kim (2012) Electrodeposition of CoPtP/Au multisegment nanowires: Synthesis and DNA functionalization. Int J Electrochem Sci 7: 7762-7769.
- E Kantar (2016) Hysteretic features of Ising-type segmented nanostructure with alternating magnetic wires. Journal of Alloys and Compounds 676: 337-346.
- Suresh Sagadevan, Kaushik Pal, Zaira Zaman Chowdhury (2017) Scalable synthesis of CdS-Graphene nanocomposite spectroscopic characterizations. Journal of Materials Science: Materials in Electronics 28: 17193-17201.
- Céspedes, MS Ferreira, S Sanvito, M Kociak (2004) Contact induced magnetism in carbon nanotubes. J Phys Condens Matter 16.
- Maria del Carmen Giménez-López, Fabrizio Moro, Alessandro La Torre, Carlos J Gómez-García, Paul D Brown, et al. (2011) Encapsulation of single-molecule magnets in carbon nanotubes. Nat Commun 2: 407.
- Hu X, Dong S (2008) Metal nanomaterials and carbon nanotubes-Synthesis, functionalization and potential applications towards electrochemistry. J Mater Chem 18: 1279-1295.
- Kaushik Pal, MLNM Mohan, Mike Foley, Waqar Ahmed (2018) Emerging assembly of ZnO-nanowires/graphene dispersed liquid crystal for switchable device modulation. Organic Electronics 56: 291-304.
- Zhuang Kang, Lixia Gu (2011) Sol-gel synthesis of multi-walled carbon nanotubes reinforced alumina-silica fibers. Journal of Macromolecular Science Part B Physics 50: 7.
- Kaushik Pal, Bihong Zhan, Xiao Ma, MLN Madhu Mohan, Guoping Wang (2016) Functionalized graphene oxide dispersed hydrogen bonded liquid crystals efficient electro-optical switching. Journal of Display Technology 12: 281-287.
- A Shirazi Tehrani, M Almasi Kashi, A Ramazani, AH Montazer (2016) Axially adjustable magnetic properties in arrays of multilayered Ni/Cu nanowires with variable segment sizes. J Superlatt Microstruct 95: 38-47.
- EA Rando, S Allende (2015) Magnetic reversal modes in multisegmented nanowire arrays with long aspect ratio. J Appl Phys 118: 013905.
- AL Gonzalez, P Landeros, AS Nunez (2010) Spin wave spectrum of magnetic nanotubes. Journal of Magnetism and Magnetic Materials 322: 530-535.
- N Zaim, A Zaim, M Kerouad (2017) Random crystal field effect on the magnetic and hysteresis behaviors of a spin-1 cylindrical nanowires. Journal of Magnetism and Magnetic Materials 424: 443-450.
- T Kaneyoshi (2016) Ising nanowires with simple core-shell structure; Their characteristic phenomena. J Phys Chem Solids 96-97: 1-9.
- M Keskin, N Sarli, B Deviren (2011) Hysteresis behaviors in a cylindrical Ising nanowires. Solid State Communication 151: 1025-1030.
- M Vasilakaki, KN Trohidou (2009) Numerical study of the exchange-bias effect in nanoparticles with ferromagnetic core/ferrimagnetic disordered shell morphology. Physical Review B 79: 144402.
- VA Tanriverdiyev (2015) Phase transition in Ising magnetic superlattice nanowires: Molecular field theory approach. Journal of Magnetism and Magnetic Materials 393: 188-191.
- TM Nguyen, MG Cottam (2006) Spin-wave excitations in ferromagnetic nanotubes. Surface Science 600: 4151-4154.
- TM Nguyen, MG Cottam (2004) A microscopic theory of the dipole-exchange spin waves in ferromagnetic nanowires. Journal of Magnetism and Magnetic Materials 272-276: 1672-1673.
- E Kantar (2018) Composition and temperature dependences in Ising-type multisegment nanostructure academic platform. Journal of Engineering and Science 6-3: 67-72.
- Youping Chen, James D Lee (2003) Determining material constants in micromorphic theory through phonon dispersion relations. International Journal of Engineering Science 41: 871-886.
- Majid Akbarzadeh Khorshidi (2020) Validation of weakening effect in modified couple stress theory: Dispersion analysis of carbon nanotubes. International Journal of Mechanical Sciences 170: 105358.
- M Shaat (2017) A general nonlocal theory and its approximations for slowly varying acoustic waves. International Journal of Mechanical Sciences 130: 52-63.
- VA Tanriverdiyev (2015) Local spin excitations in the rectangular ferromagnetic semiconductor nanowires. FNT 41: 363-367.
- HT Diep (1989) Effects of quantium fluctuations in anti ferromagnetic super lattices at low temperatures. Phys Lett A 138: 69-72.
- R Schiller, W Nolting (1999) Temperature-dependent band structure of a ferromagnetic semiconductor film. Phys Rev B 60: 462-471.
- Callen HB (1963) Green function theory of ferromagnetism. Phys Rev B 130: 890.
- T Kaneyoshi (2011) Magnetic properties of a cylindrical Ising nanowire or nanotube. Phys Status Solidi B 248: 250-258.
Author Details
VA Tanriverdiyev*
Institute of Physics of the National Academy of Sciences of Azerbaijan, Azerbaijan
Corresponding author
VA Tanriverdiyev, Institute of Physics of the National Academy of Sciences of Azerbaijan, Baku Az -1143, Baku, H.Javid ave.33, Azerbaijan.
Accepted: May 19, 2020 | Published Online: May 21, 2020
Citation: Tanriverdiyev VA (2020) Spin-Waves Excitations in Segmented Nanotubes Consisting of Ferromagnetic and Non-Magnetic Materials. Int J Nanoparticles Nanotech 6:035.
Copyright: © 2020 Tanriverdiyev VA. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In the present study, magnetization and dispersion relations of spin-waves propagating along a segmented nanotube constructed of atomic layers of ferromagnetic and non-magnetic materials are considered by use of the Green function method. Within the framework of random-phase approximation, the expression of Green functions for different spins of segmented nanotubes, which is modeled as having a hexagonal cross section are derived. The effects of the composition (p) and exchange couplings on spin-wave spectra and temperature dependence of magnetization are investigated in detail. It was found that small magnetization is observed in the system at small values of parameter p and exchange constants, and the critical temperature at which second-order phase transition occurs is low. When the obtained theoretical results compare with some other works, a very good agreement between them is observed.
PACS: 75.70. Ak
Keywords
Spin-waves, Multisegment nanostructure, Green function
Introduction
Nanostructured materials have attracted intense research interest over recent years, as they provide the critical building blocks for the booming nanoscience and nanotechnology. The reason of this fact is that they often exhibit new and enhanced properties over their bulk counter parts and have potential for applications in magneto electronic devices [1-3]. Recent progresses on magnetism and magnetic materials have made magnetic nanostructures a particularly interesting class of materials for both scientific and technological explorations. Precise control of the structural parameters, such as size, composition, orientation, and assembly of materials with nano-scaled dimensions is of importance to obtain the desired functional properties and device performance [4-5]. Among these structures, multisegmented nanostructures represent a unique platform towards the important application in multiplexed bioanalysis, biosensors, magnetic cell separation and gene delivery with multiple functionality [6]. As a rule, there are two types of morphologies in multicomponent nanostructures: Radial structures, such as the core/shell type, and axial structures, namely the segmented type. Magnetic multisegment nanostructures increased due to their multifunctional and structural advantages over their analogues, single-component nanostructures. Segmented nanostructures are mainly concentrated on two segments of nanowires, nanotubes and nanowire/nanotube segment [7,8].
Physicists have shown that carbon nanotubes can become magnetized when they are placed in contact with a magnetic material [9]. The chemical combination of magnetic nanocrystals and carbon nanotubes in order to obtain nanohybrid structures, follows various strategies: encapsulation of magnetic molecules inside the carbon nanotubes or grafting/decorating carbon nanotubes on their surface by bioconjugation chemistry or electrochemical deposition [10,11]. Another process used in the fabrication of magnetic nanocomposite structures, as well as nanotubes in conjunction with templates is the so called sol-gel process. It consists of a wet-chemical technique for the fabrication of materials starting either from a chemical solution or colloidal particles to produce an integrated network [12-14].
Multisegmented structures makes one able to control the magnetization of either each segment or the array as a whole for taking advantage of small magnetic bits for different applications. Therefore, properties of these systems, such as segmented nanowires and nanotubes are of particular importance, both from the experimental and from the theoretical point of view for many scientists [15-18]. Theoretically, the magnetic properties of these structures are actively studied by using different methods, such as mean-field approximation, effective-field theory, Monte-Carlo simulations, Bethe-Pierls approximation and Green function technique (GF) [19-21]. The model in order to investigate the magnetic properties of nanostructured systems has an important role in the deeper understanding of behaviors in magnetic systems. Generally, various multicomponent nanostructures can be modeled as having a chosen shape with a finite number of spins arranged [22-24]. The magnetic behavior of nanoscale magnetic objects is strongly dependent on size, shape and composition. There have been a few works where the Ising system is used to investigate magnetic properties of segmented nanostructure [7,25].
There is still a great amount of attention devoted to realize new physics and engineering application of this type of segmented nanostructure. Dispersion relations describe the effect of dispersion on the properties of waves in a medium. The study of dispersion relation is very useful in determining the fundamental parameters that characterize these structures [17,23,26-28].
The aim of this paper is to discuss the effects of composition and temperature on the spin-waves excitations of nanotubes with ferromagnetic/non-magnetic segments. This paper is organized as follows. In section 2, the model and formalism of the GF is presented. Section 3 is devoted to detailed numerical results and discussions. Finally, Section 4 is devoted to a summary and a brief conclusion.
Model and Formulation
As indicated in Figure 1 we consider a hexagonal segmented nanotubes (HSNT) model in which atomic layers of ferromagnetic (FM) material alternate atomic layers of non-magnetic (NM) material. Each atomic layer is assumed to be the xy plane.
The Hamiltonian of the system can be written in the form
In here, and describes exchange interactions between the neighboring spins and Zeeman’s energy in FM and NM segment, respectively. Also, h is externally applied field in the along the nanotubes under consideration and it is assumed to be parallel to the axis z. Intersegment interaction is described by the term . The exchange couplings between spins in intrasegment and intersegment are assumed to be J and , respectively. The parameter is a site occupancy number that is 1 or 0, depending on the whether the site is occupied or not. Since only the NM segment is diluted in the present system, takes unity with a probability p when the site i is occupied by a FM atom and takes 0 with a probability when the site i on the NM segment is occupied by a NM atom.
Employing the equation of motion for the GF [29] one obtains the following system of equations
Here, n and m are layer indices, while 1,2...,6 and are label the position of the spins in layers n and m respectively. On the other hand and .
The total wave vector has two components . Component k and q characterize the periodicity of the HSNT along the axis and circumferential direction, respectively. The system is periodic in the z direction, which lattice constant is . Therefore, the wave-vector component, denoted as k takes continuous values, and is within the first Brillion zone. The other component denoted as q takes the following discrete values.
The higher order GF appearing in the system of equations (3) is decoupled random-phase-approximation (RPA). This is complex to employ the system of equations (3) for the HSNT in the general case. It has taken into account the periodic condition of the system one can we introduce two type Fourier transformation of GF:
Using (5) and (6) the GF are obtained by solving the equations (3):
The poles of the GF occur at frequencies, which are the roots of the spin wave dispersion equation for HSNT under consideration:
Where
For the HSNT depicted in Figure 1, there exist two magnetizations ( and ) in the z direction.
Solving the average spin, we derive the correlation function using the spectrum theorem [30,31]
Here, , is the Boltzmann constant, T is the temperature. Using (7), (8) and the relation to obtain the imaginary part of the Green functions, one finally obtains [31]
According to the theory of Callen [32] the average spin can be calculated using the following equation
Where
The total average spins of per site of the nanowire under concentration can be calculated as
Now the equation (10) and (11) can be solved self consistently to obtain the average spin at any given temperature.
If
Numerical Results and Discussions
The expression of frequencies given (9) and (10) are one of the main results of this paper. It can be verified from these expressions that when both media consist of FM atoms ( ) they reduce the expressions for ferromagnetic nanotubes (FNTs). In Figure 2a and Figure 2b spin-wave spectra for reduced frequency versus illustrated for particular choice of parameters. The frequencies for the lowest branches are not zero at . Easily, it can be explained by applied external magnetic field. The spin wave frequencies increase with increasing wave vectors and exchange coupling between spins. On the other hand, with increasing value of spin wave frequencies increase.
In Figure 3, we have shown the temperature dependence of magnetization in HSNT under consideration. The spontaneous magnetization of the spins is at zero temperature. The curves correspond for each segment and total magnetizations with and . In each case, the total spin magnetization has the middle value. Magnetization of the spins labeled n (for FM segment) is smaller than that of the spins labeled f (for NM segment). This can be explained by the fact that the magnetic atoms in each segment have different nearest neighbors. So that, if site occupied by magnetic atom in NM segment, it always interacts with the magnetic atoms of FM segment. However, depending on the value of p, the magnetic atom in FM segment may be the nearest-neighbor to the non-magnetic atom of NM segment. Therefore, spins labeled f canted more slightly than the spins labeled n with respect to nanotubes axes. Also, analysis shows that total magnetization of HSNT is smaller than pure FNT.
Conclusion
In this paper, we have presented magnetic properties of multisegmented nanotube with ferromagnetic/non-magnetic structure. The effects of the exchange couplings and probability to the spin excitations are clarified. Some characteristic phenomena are found in the spin-wave spectra and temperature dependence of magnetization. Average spin is calculated using the theory of Callen.
Analysis shows that the number of the spin wave branches in HSNT is two times more than pure FNTs. So, it observed eight branches in the HSNT and four branches in FNT. In spite of the fact, there are six spins in the intralayer of the FNTs, but four dispersion branches arise. Easily, it can be explained by the set of all symmetry operations. Spin wave-branches move up with increasing exchange interactions and probability p.
Moreover, it is found that magnetization decrease to zero continuously as the temperature increases; therefore, a second-order phase transition occurs.It was found that stronger magnetization is observed in the system at high values of parametr p and exchange constants. Therefore, transition temperature increases as the values of p increases. These results are consistent with some similar theoretical results [25,33].

