International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5068/6518
Simulated Thermomagnetic Properties of Dyal2, Hoal2 and Eral2 Compounds in Comparison with the Results for Tbal2, Gdal2 and Smal2 Calculated by ATOMIC MATTERS MFA Computation System
R Michalski1* and J Zygadło1,2
Table of Content
Figures
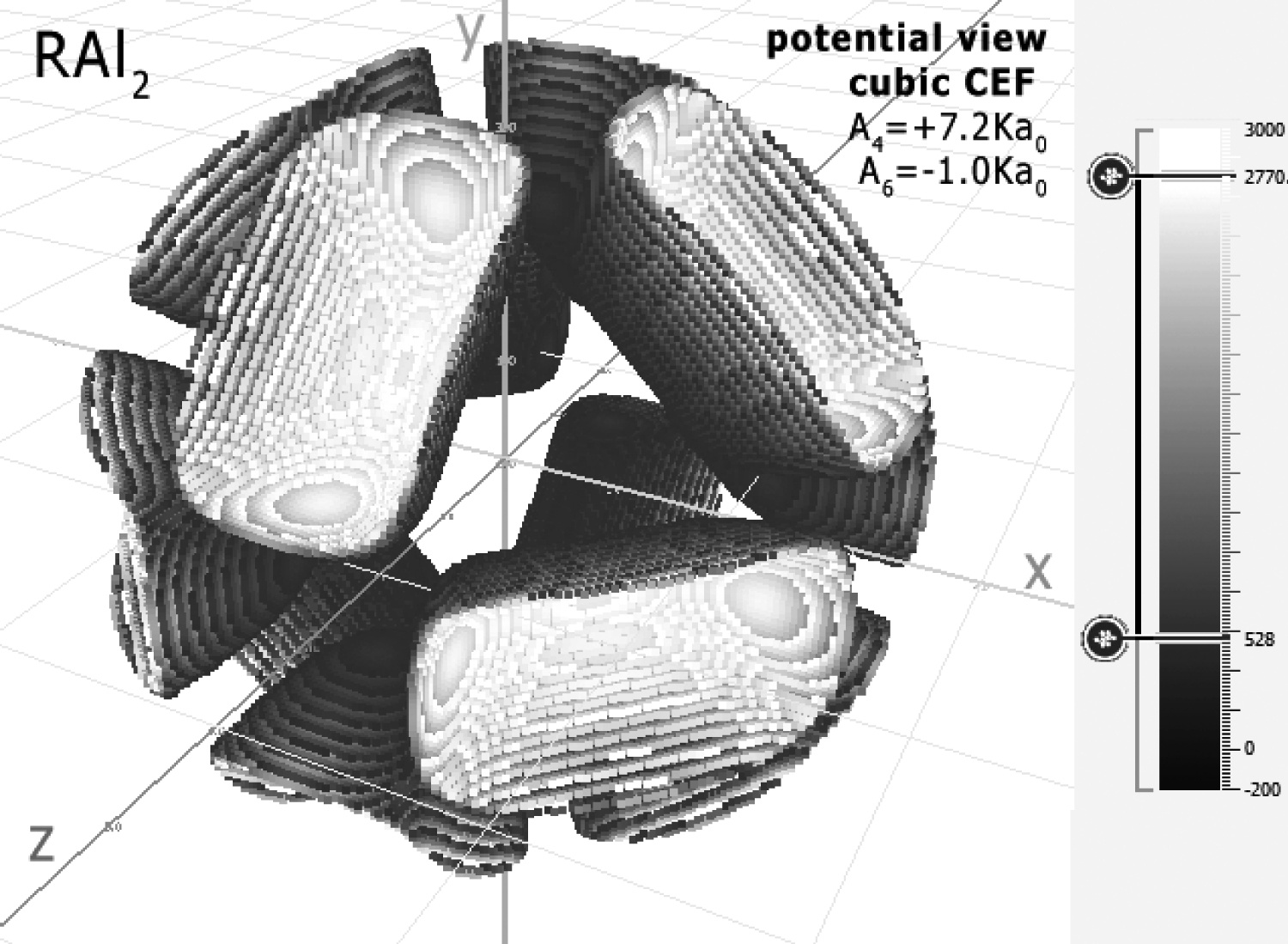
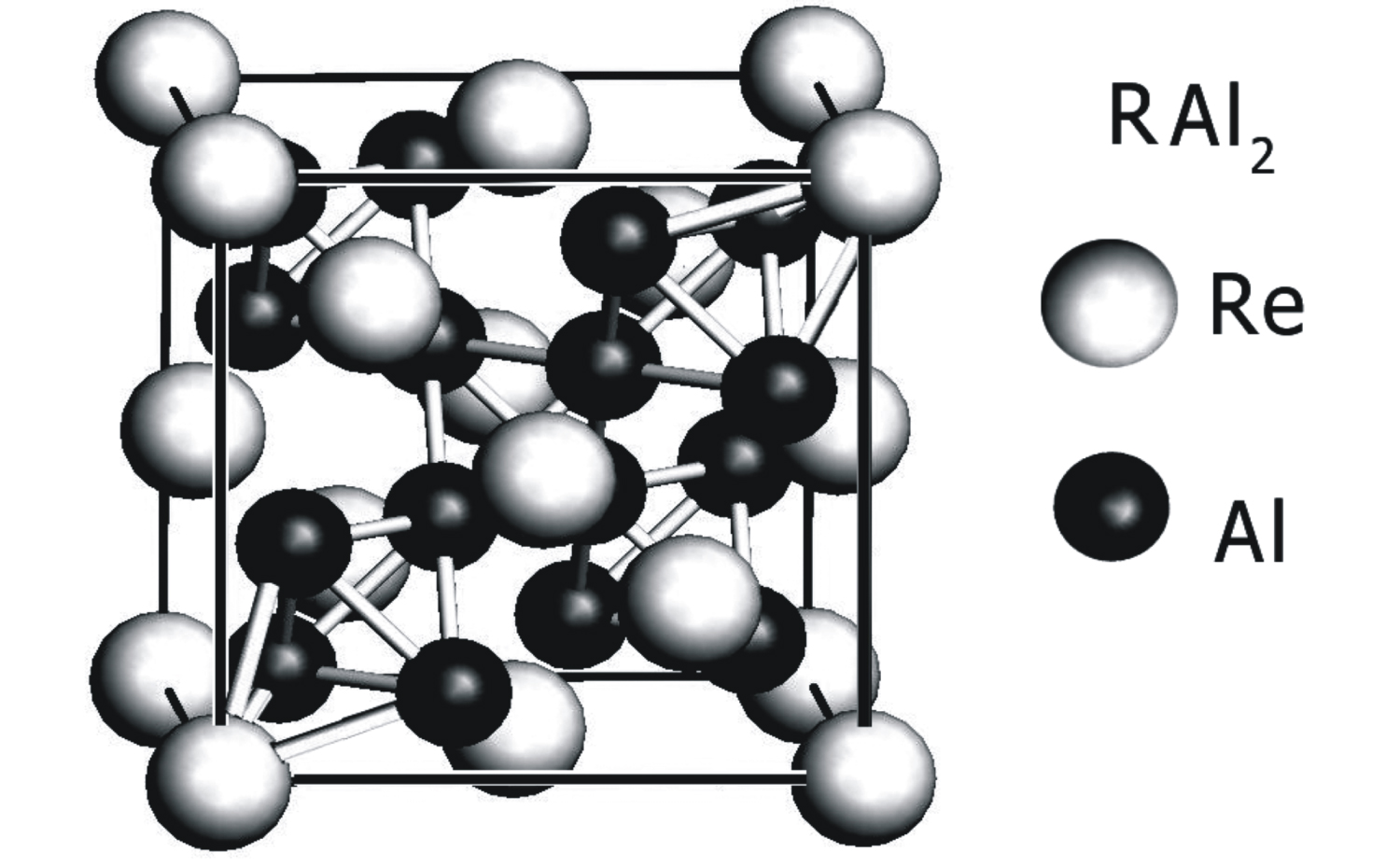
Figure 1: Crystal Field potential visualization of...
Crystal Field potential visualization of cubic surrounding of R-ions in RAl2 defined by CEF parameters: A4 = +7.164 Ka0 and A6 = -1.038 Ka0. The visualization of positive sign potential is cut off by the sphere.
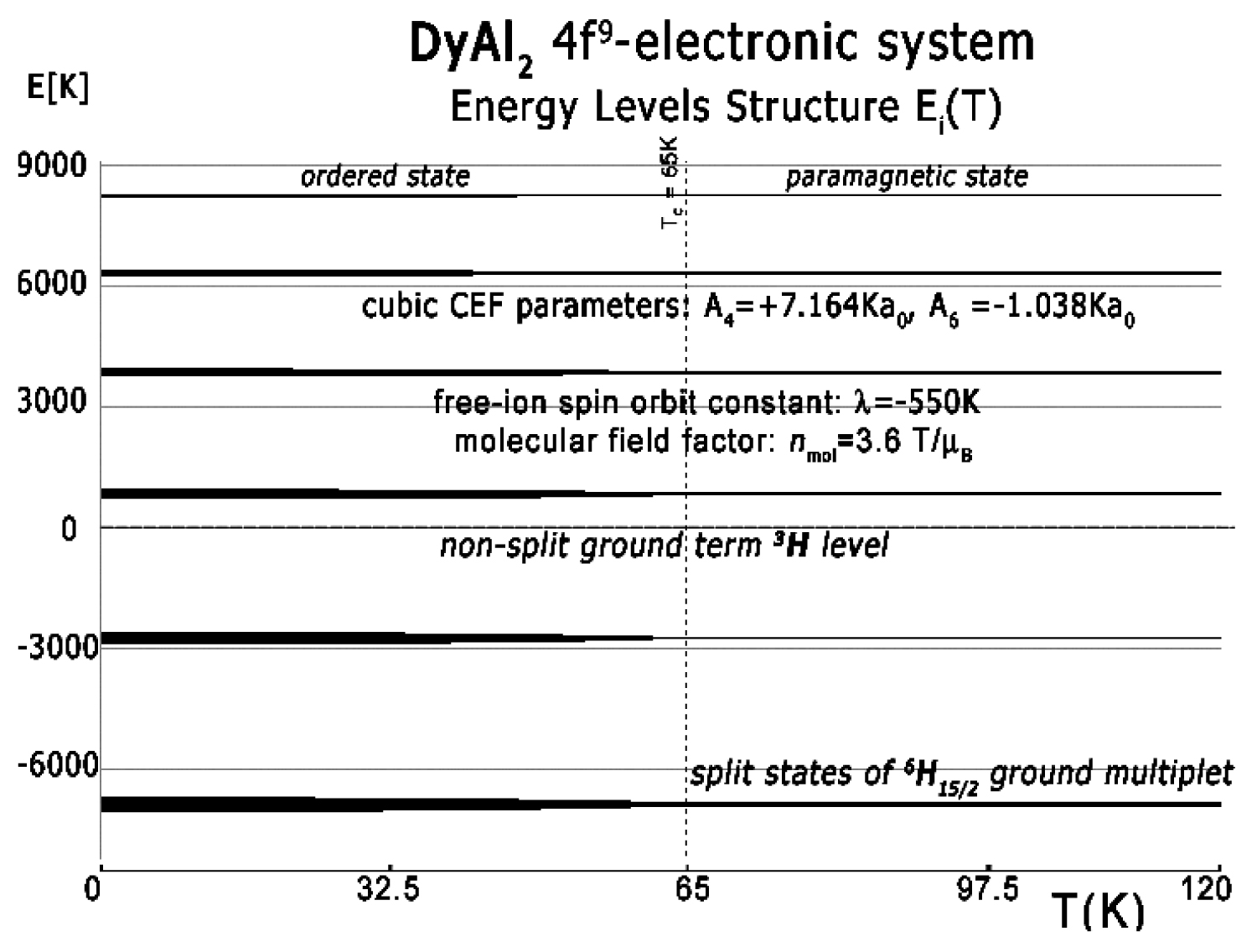
Figure 3: The result of calculation of energy level...
The result of calculation of energy level position vs. temperature of the fine electronic structure of 4d9 electronic configuration of Dy ions in DyAl2 in |L,S,Lz,Sz> space under the influence of intra-atomic spin-orbit coupling, inter-atomic self-consistent molecular magnetic field and Crystal Electric Field (CEF).

Figure 4: Ground multiplet energy level structure...
Ground multiplet energy level structure vs. temperature calculated for 4f9 electronic system of Dy ions in DyAl2. At Curie temperature TC = 65 K the structure splits under the influence of molecular field and CEF.

Figure 5: Ground energy level structure vs. temperature...
Ground energy level structure vs. temperature calculated for 4f9 electronic system of Dy ions in DyAl2 under the influence of external magnetic field Bext = 1 T applied along the [100] direction. Parameters of CEF used in calculations and molecular field factor are shown.
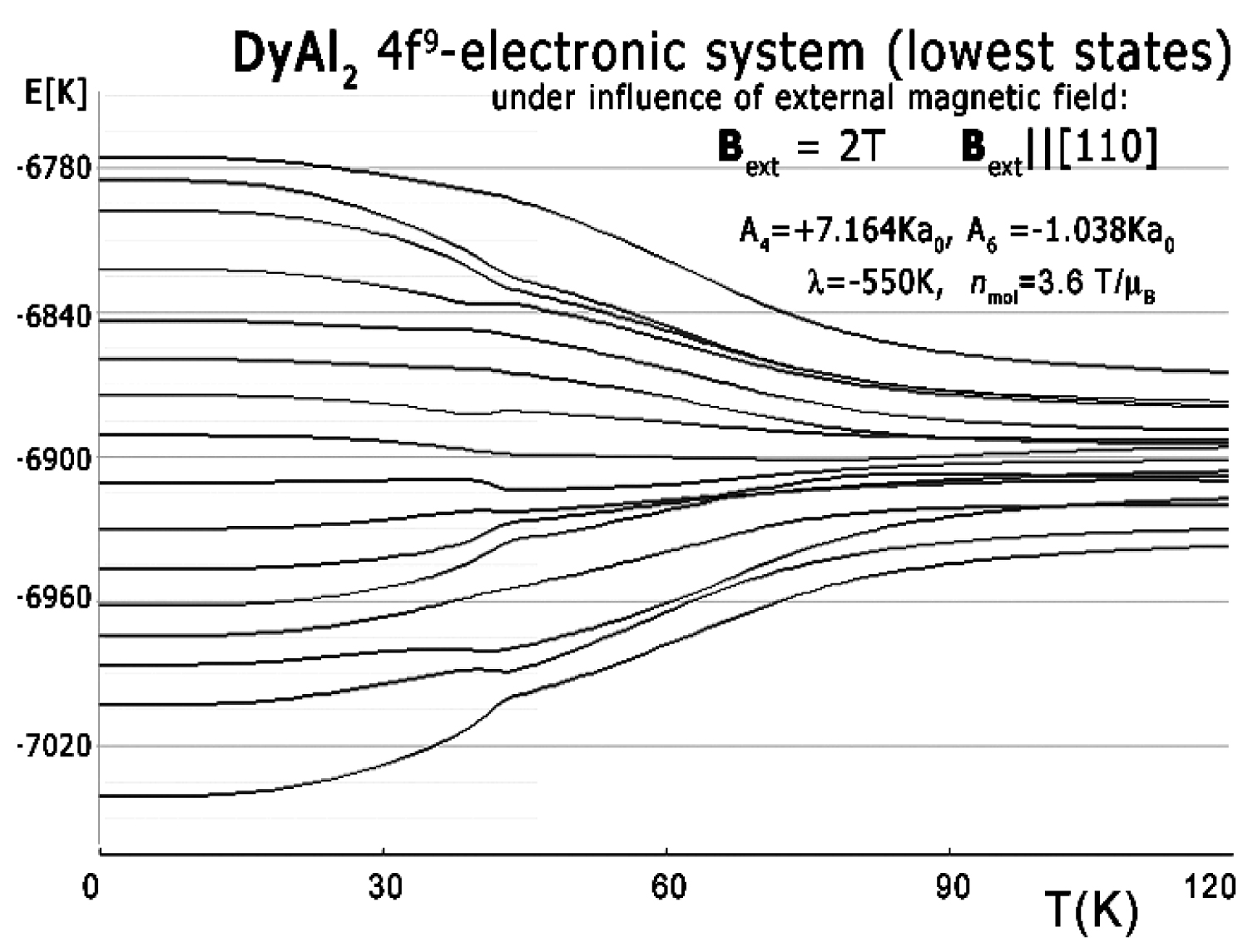
Figure 6: Ground energy level structure vs....
Ground energy level structure vs. temperature calculated for 4f9 electronic system of Dy ions in DyAl2 under the influence of external magnetic field Bext = 2 T applied along the [110] direction. Parameters of CEF used in calculations and molecular field factor are shown.
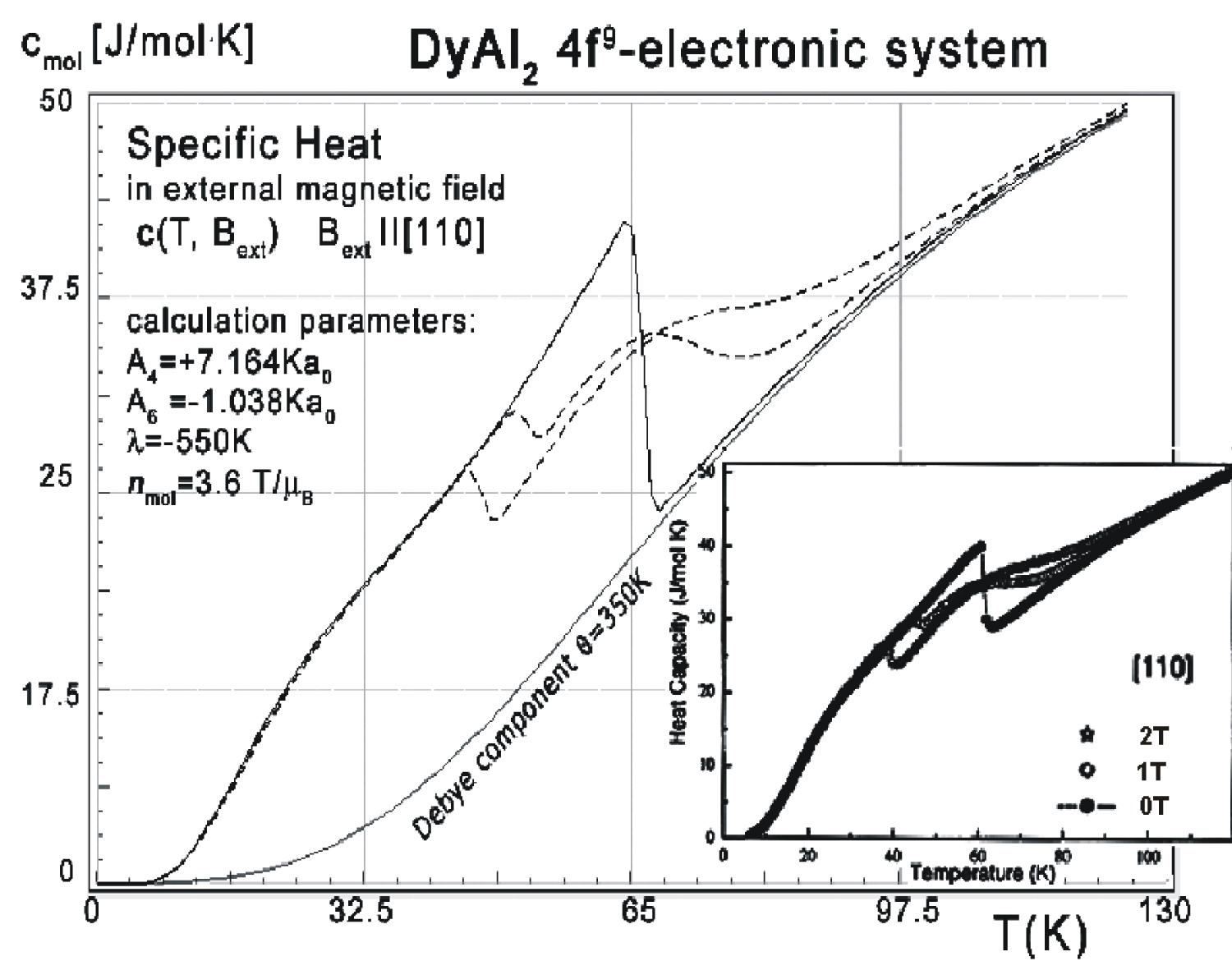
Figure 7: Calculated 4f-electron component of...
Calculated 4f-electron component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature for Dy ions in DyAl2 under the influence of an external magnetic field applied along the [110] direction. For comparison, the inset shows experimental data from [3] captured in the same external magnetic field conditions as simulated.
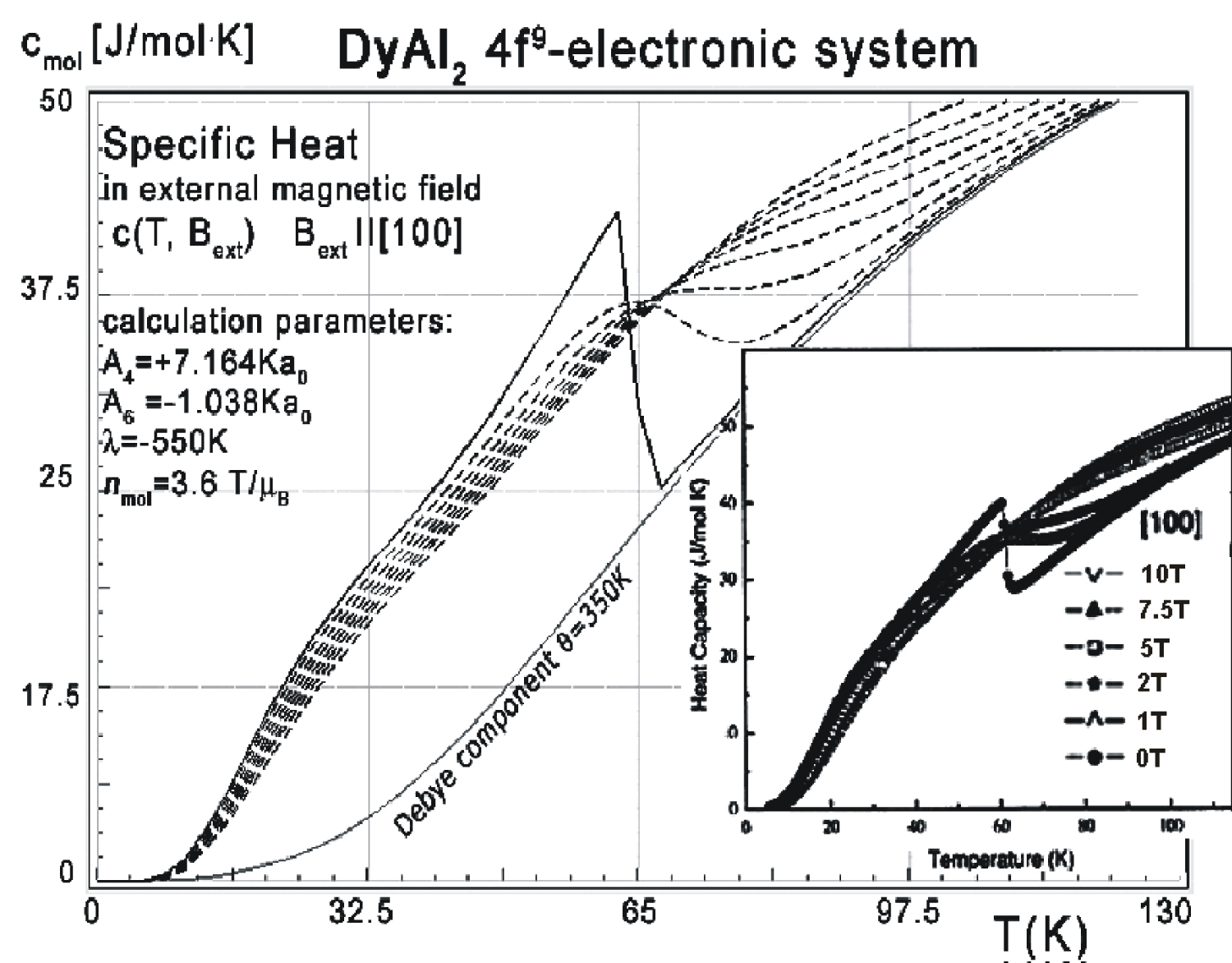
Figure 8: Calculated 4f-electron component of...
Calculated 4f-electron component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature of Dy ions in DyAl2 under the influence of an external magnetic field applied along the [100] direction. For comparison, the inset shows experimental data from [3] captured in the same external magnetic field conditions as simulated.
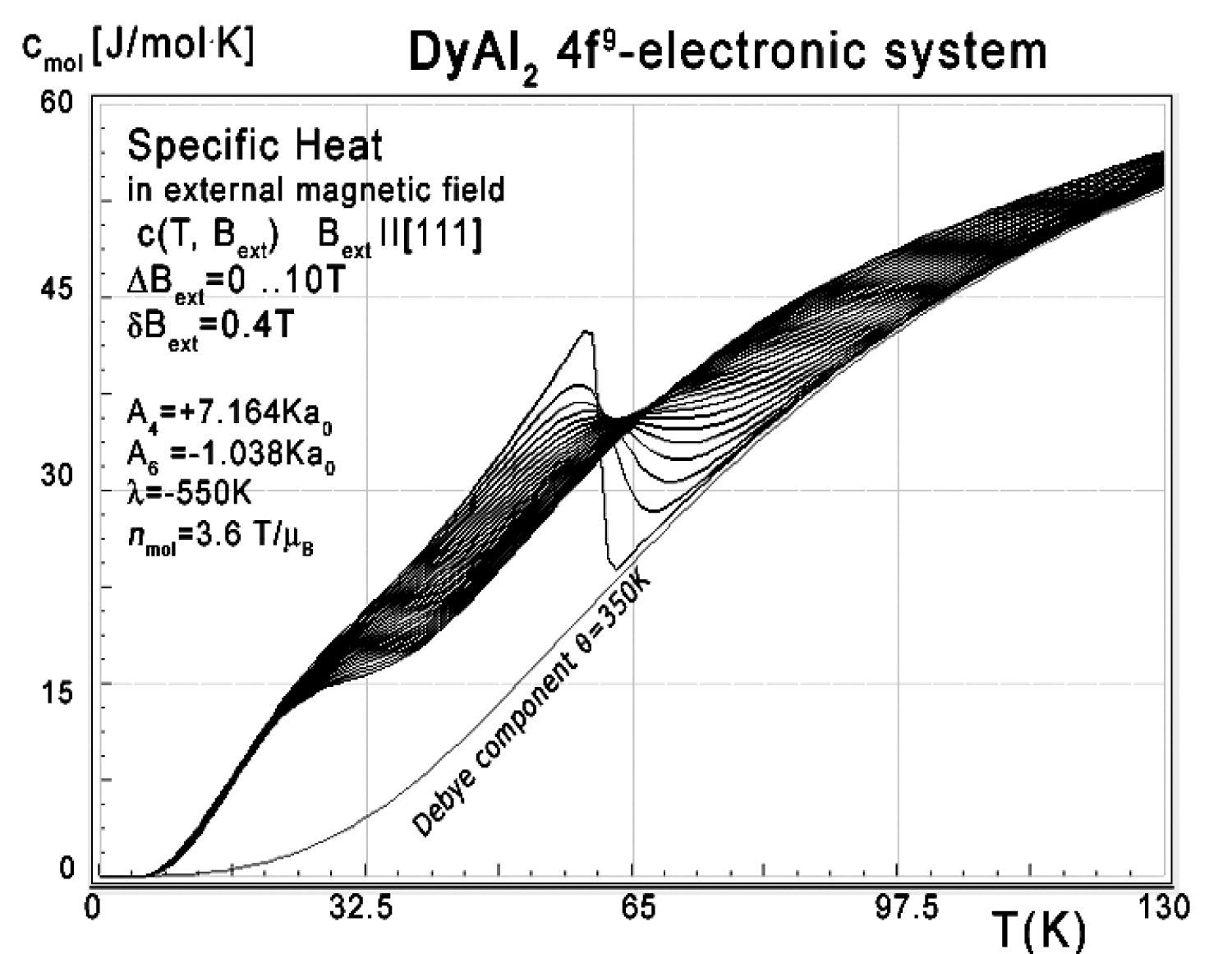
Figure 9: Calculated 4f-electron component...
Calculated 4f-electron component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature of Dy ions in DyAl2 under the influence of an external magnetic field Bext from 0 to 10 T applied along the [111] direction.
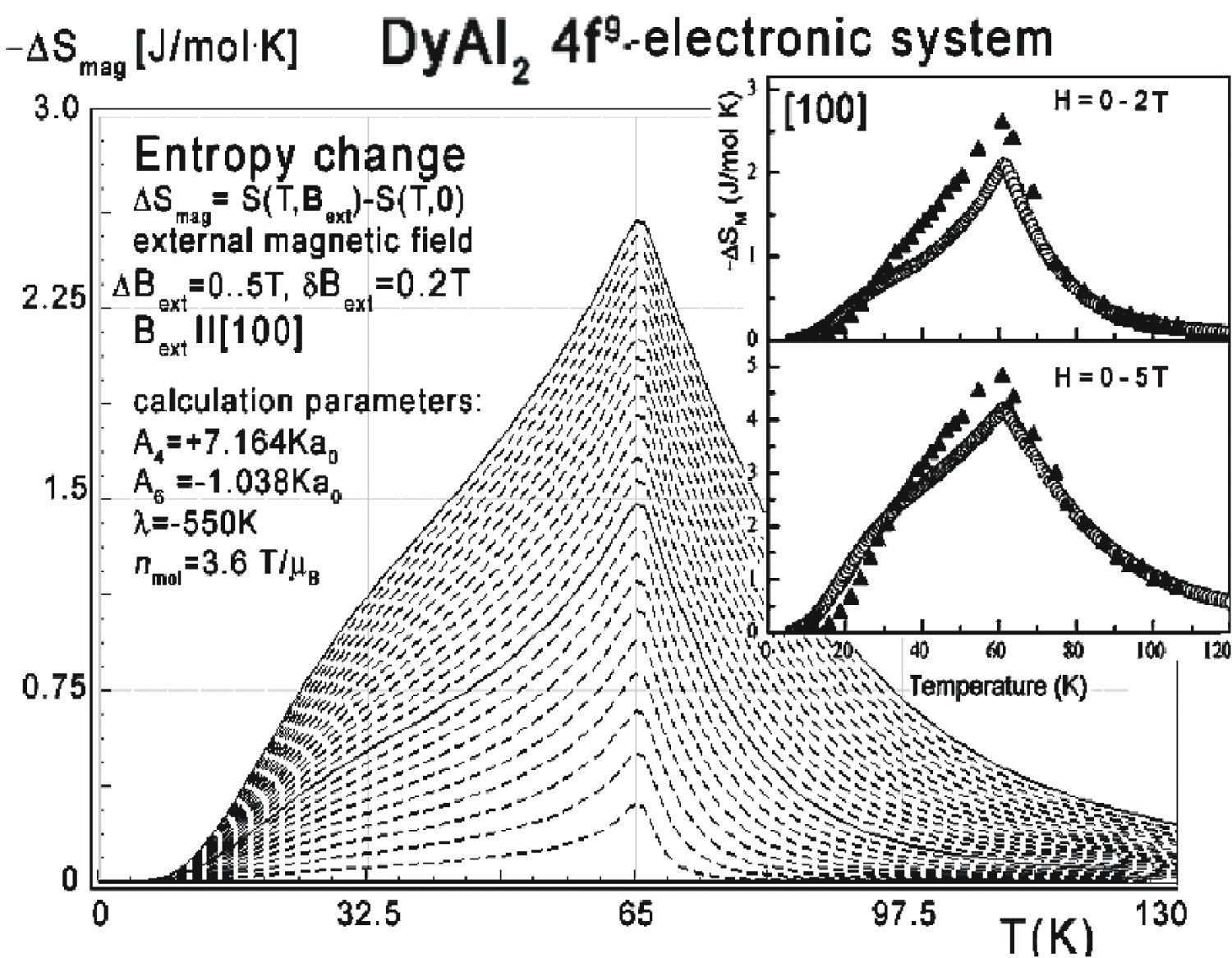
Figure 10: Calculated isothermal entropy change...
Calculated isothermal entropy change of 4f-electronic system vs. temperature (16) of Dy ions in DyAl2 under the influence of various values of external magnetic field from 0 to 5 T with step 0.2 T applied along the [100] direction. Inset: Isothermal entropy change obtained from experimental data; black triangles - extracted from the magnetization, circles - extracted from specific heat, for the DyAl2 single crystal aligned along the same direction, taken from [3]. The solid lines are congruent with the experimental data calculated for the Bext = 2 T and Bext = 5 T.
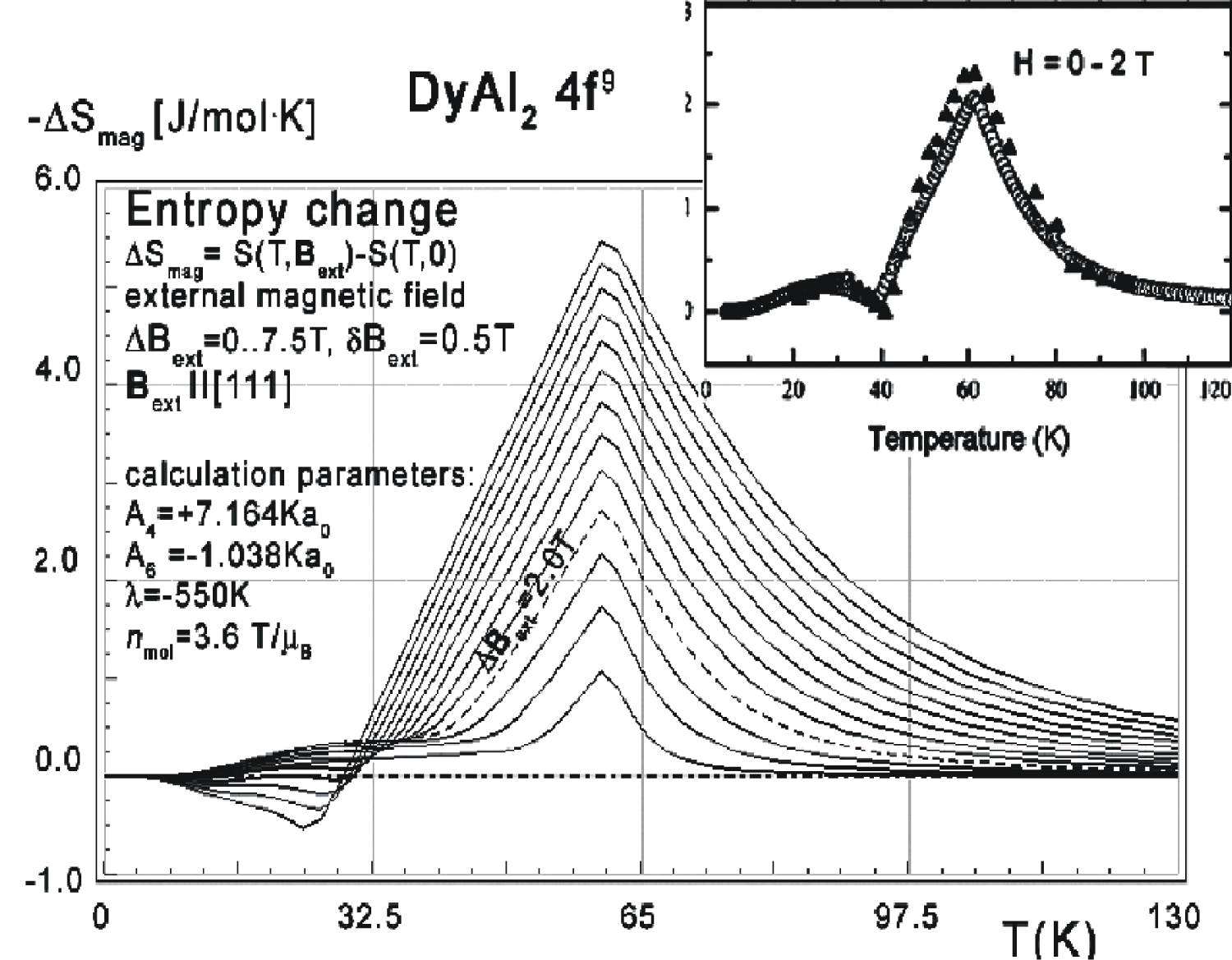
Figure 11: Calculated isothermal entropy change...
Calculated isothermal entropy change vs. temperature (16) for various values of external magnetic fields from 0 to 2 T with step 0.1 T, applied along the [110] direction of DyAl2 crystal lattice. Inset: Black triangles show isothermal entropy change obtained from experimental data extracted from the magnetization; empty circles show specific heat for a DyAl2 single crystal aligned along the same direction, taken from [3].
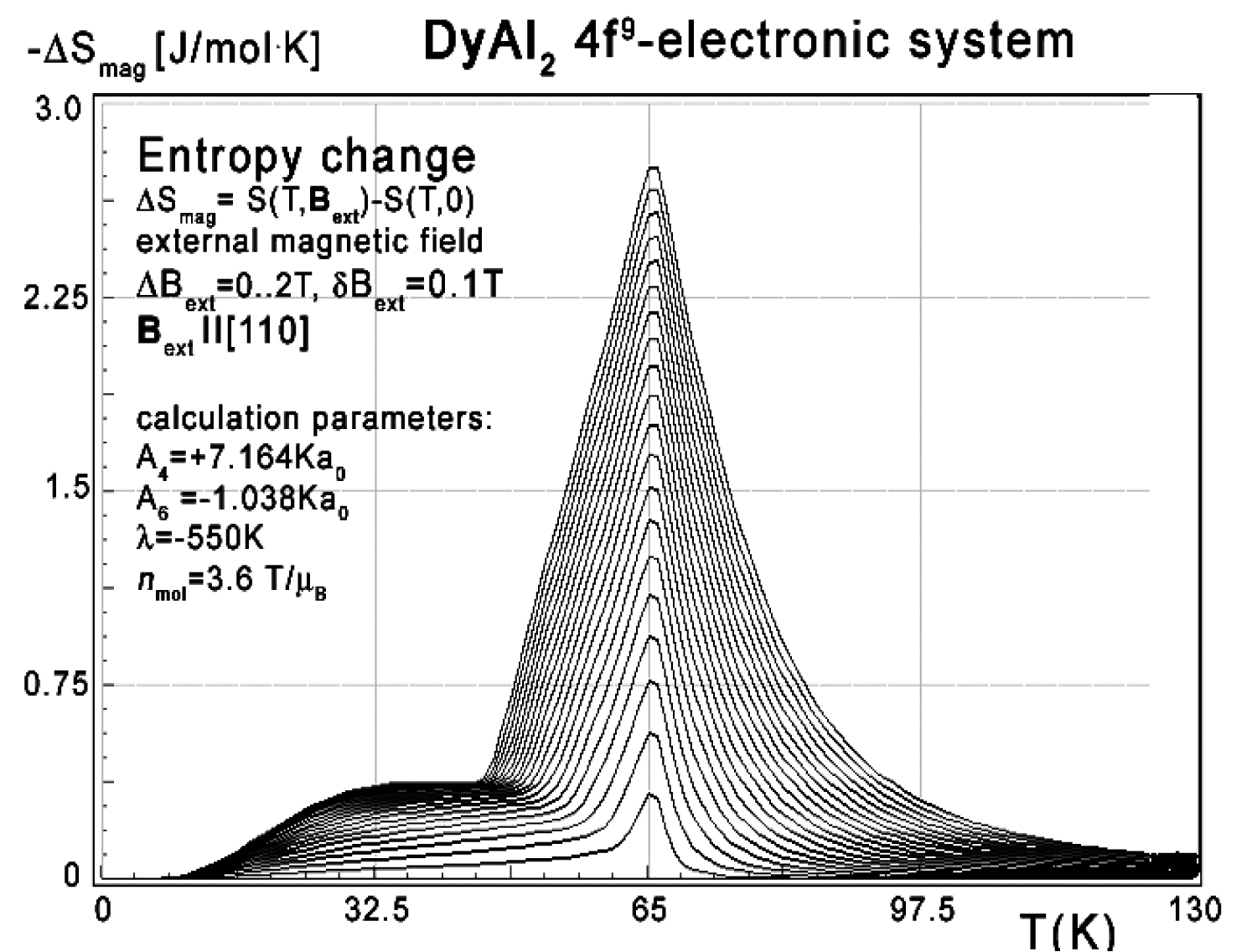
Figure 12: Calculated isothermal entropy change...
Calculated isothermal entropy change of DyAl2 vs. temperature (16) for various values of external magnetic field from 0 to 2 T with step 0.1 T applied along the diagonal [110] direction.
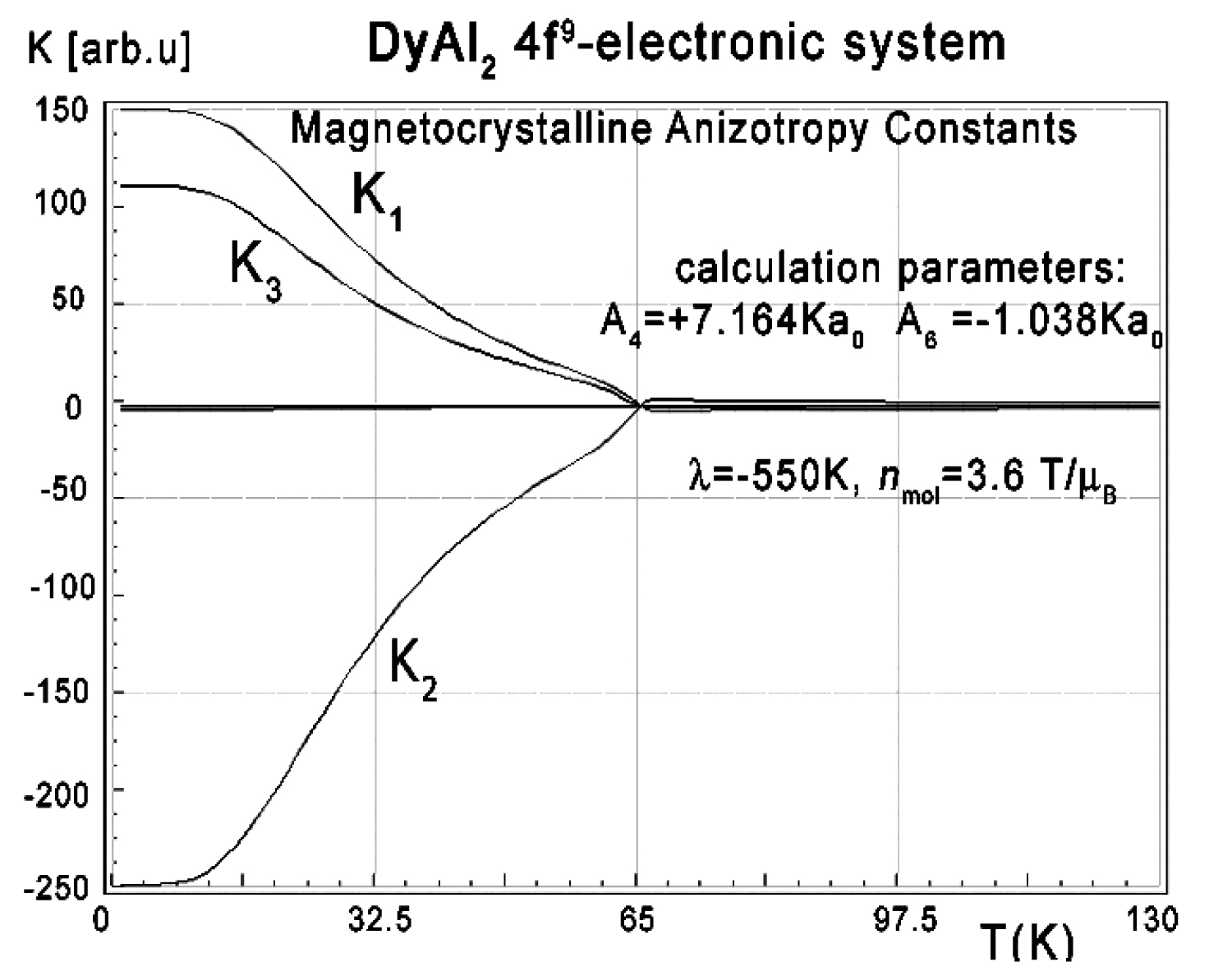
Figure 13: Calculated according to (17), magnetocrystalline...
Calculated according to (17), magnetocrystalline anisotropy constants K1, K2 and K3 vs. temperature, calculated for Dy ions in DyAl2 under the influence of CEF and molecular magnetic field.
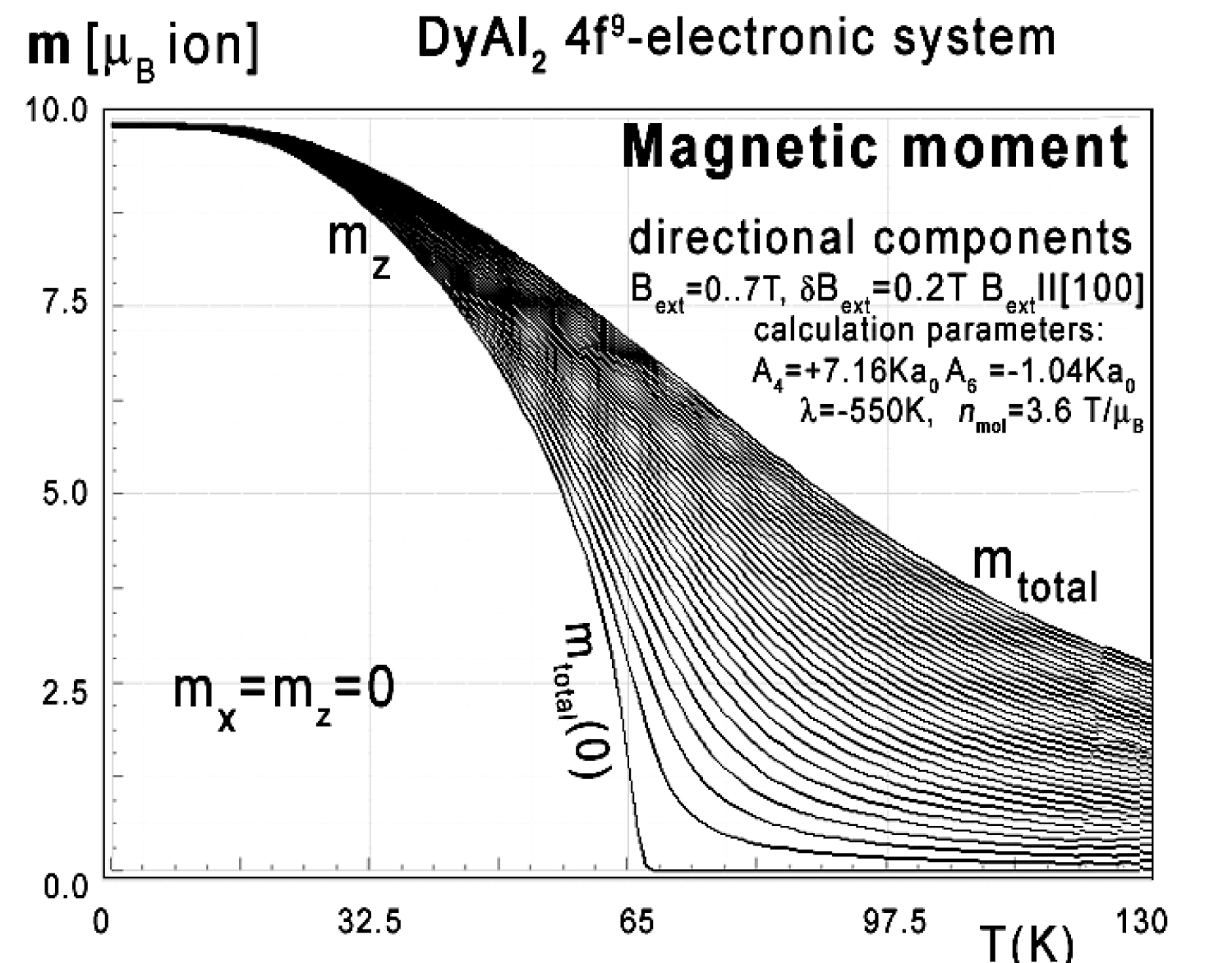
Figure 14: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment vs. temperature, calculated for Dy ions in DyAl2 under the influence of CEF and molecular magnetic field and various values of external magnetic field from 0 to 7 T with step 0.2 T applied along the [100] direction.

Figure 15: Calculated x components (solid lines)...
Calculated x components (solid lines), z-components (dashed lines) of total magnetic moment mtotal (dotted lines) vs. temperature calculated for Dy ions in DyAl2 under the influence of CEF, molecular magnetic field, and various values of external magnetic field from 0 to 7 T with step 0.2 T applied along the [110] direction.
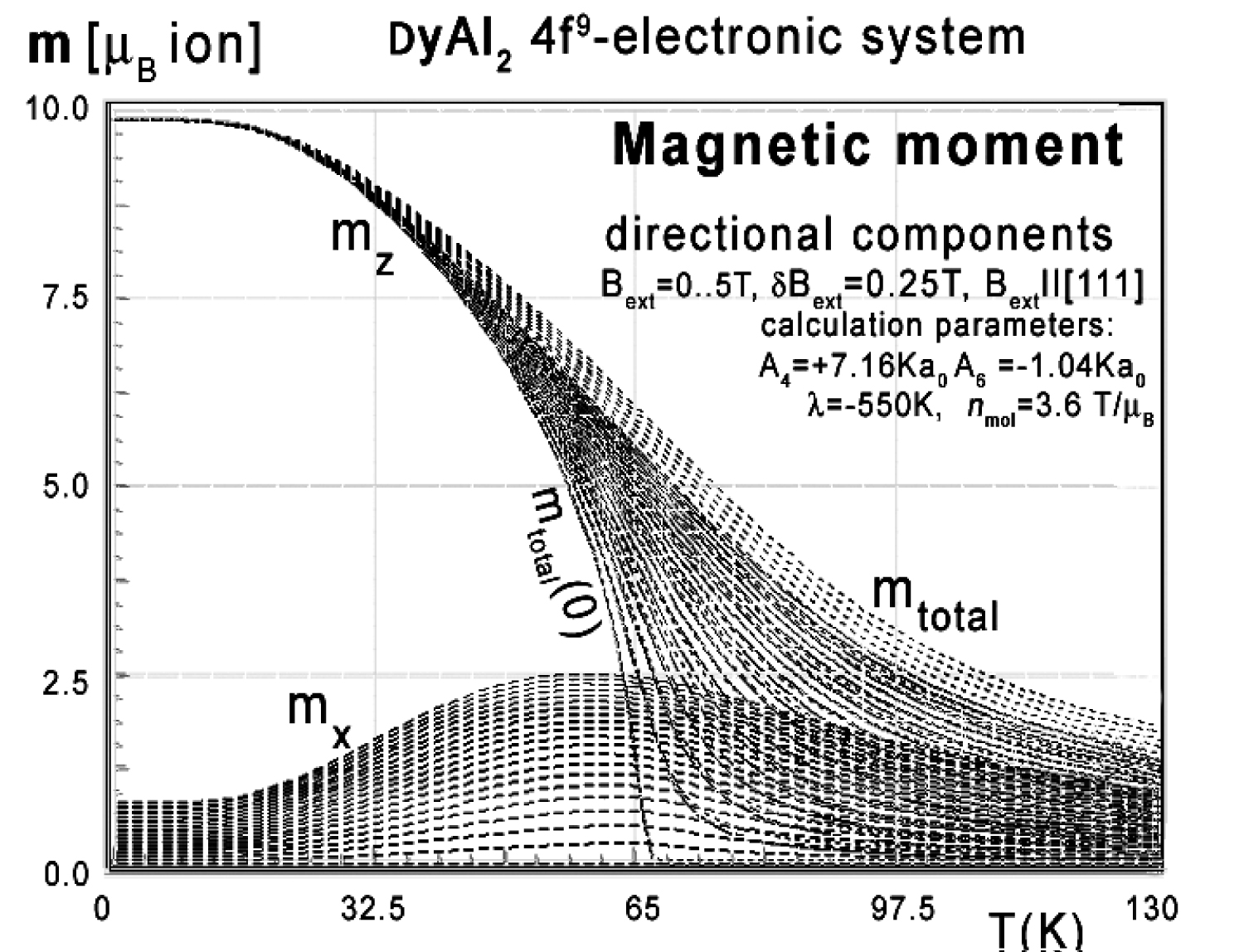
Figure 16: Calculated x components (solid lines)...
Calculated x components (solid lines), z-components (dashed lines) of total magnetic moment mtotal (dotted lines) vs. temperature, calculated for Dy ions in DyAl2 under the influence of CEF, molecular magnetic field, and various values of external magnetic field from 0 to 7 T with step 0.2 T applied along the [111] direction.
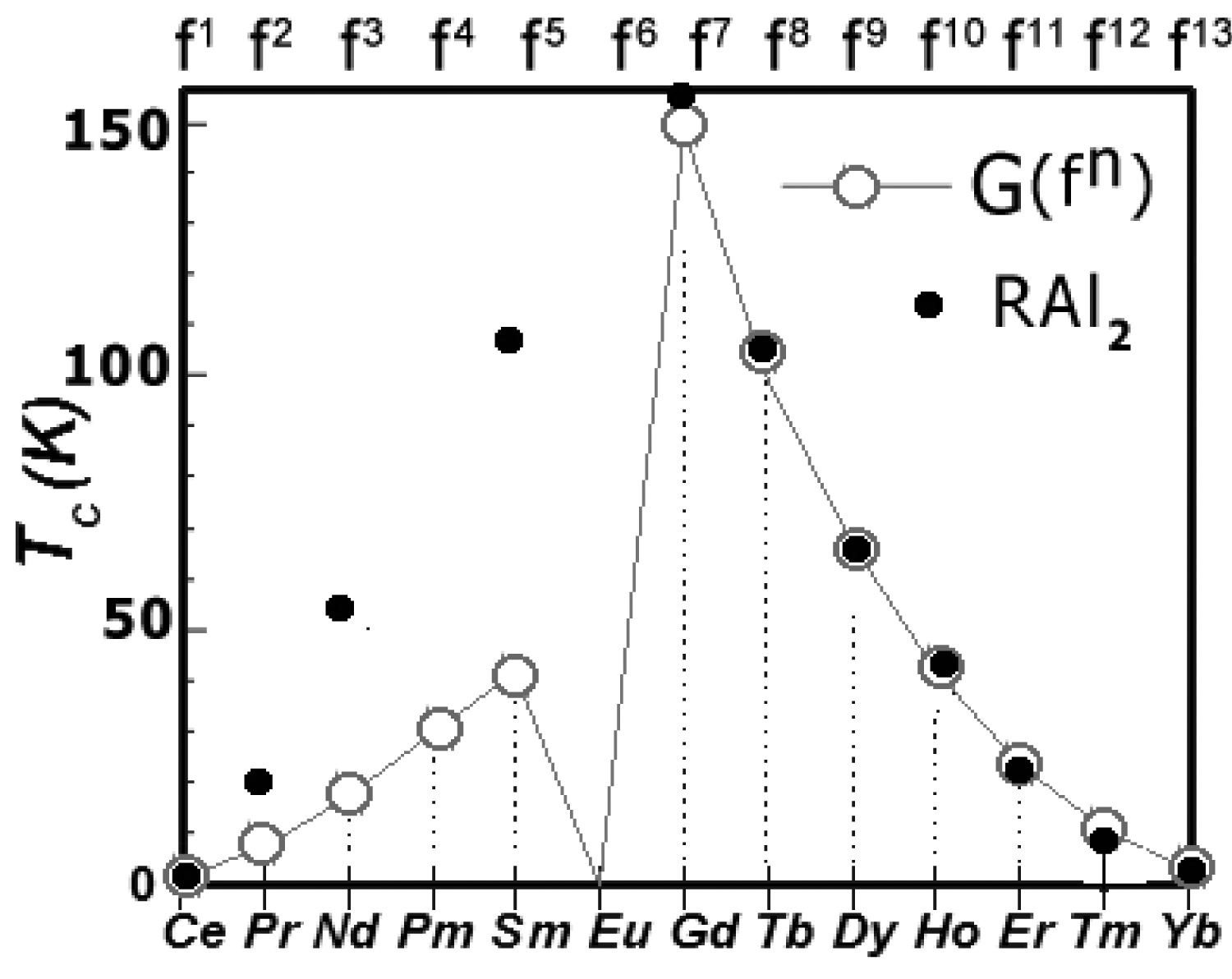
Figure 17: De Gennes scaling of Curie temperature...
De Gennes scaling of Curie temperature TC for all rare-earth ions in series RAl2 in comparison to experimental data from [4].

Figure 18: The result of calculation of ground...
The result of calculation of ground multiplet energy levels structure vs. temperature calculated of 4f10 electronic configuration of Ho ions in HoAl2 in |L,S,Lz,Sz>. At Curie temperature TC = 36 K the structure splits under the influence of a molecular field.
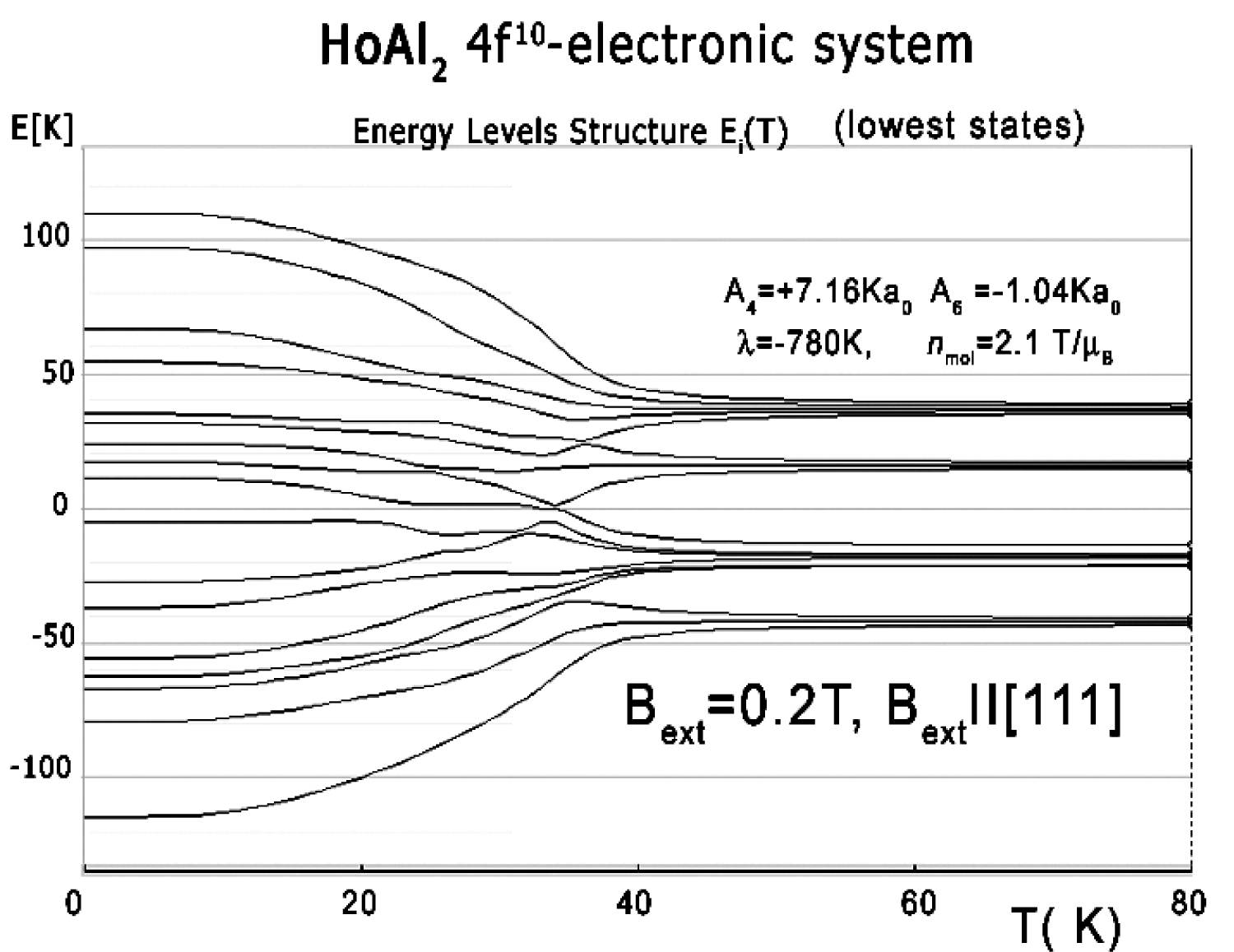
Figure 19: Ground multiplet energy levels structure...
Ground multiplet energy levels structure vs. temperature calculated for 4f10 electronic system of Ho ions in HoAl2 under the influence of a small external magnetic field of 0.2 T applied along the [111] crystal direction.

Figure 20: Ground multiplet energy levels...
Ground multiplet energy levels structure vs. temperature calculated for 4f10 electronic system of Ho ions in HoAl2 under the influence of a small external magnetic field of 0.2 T applied along the [111] crystal direction.
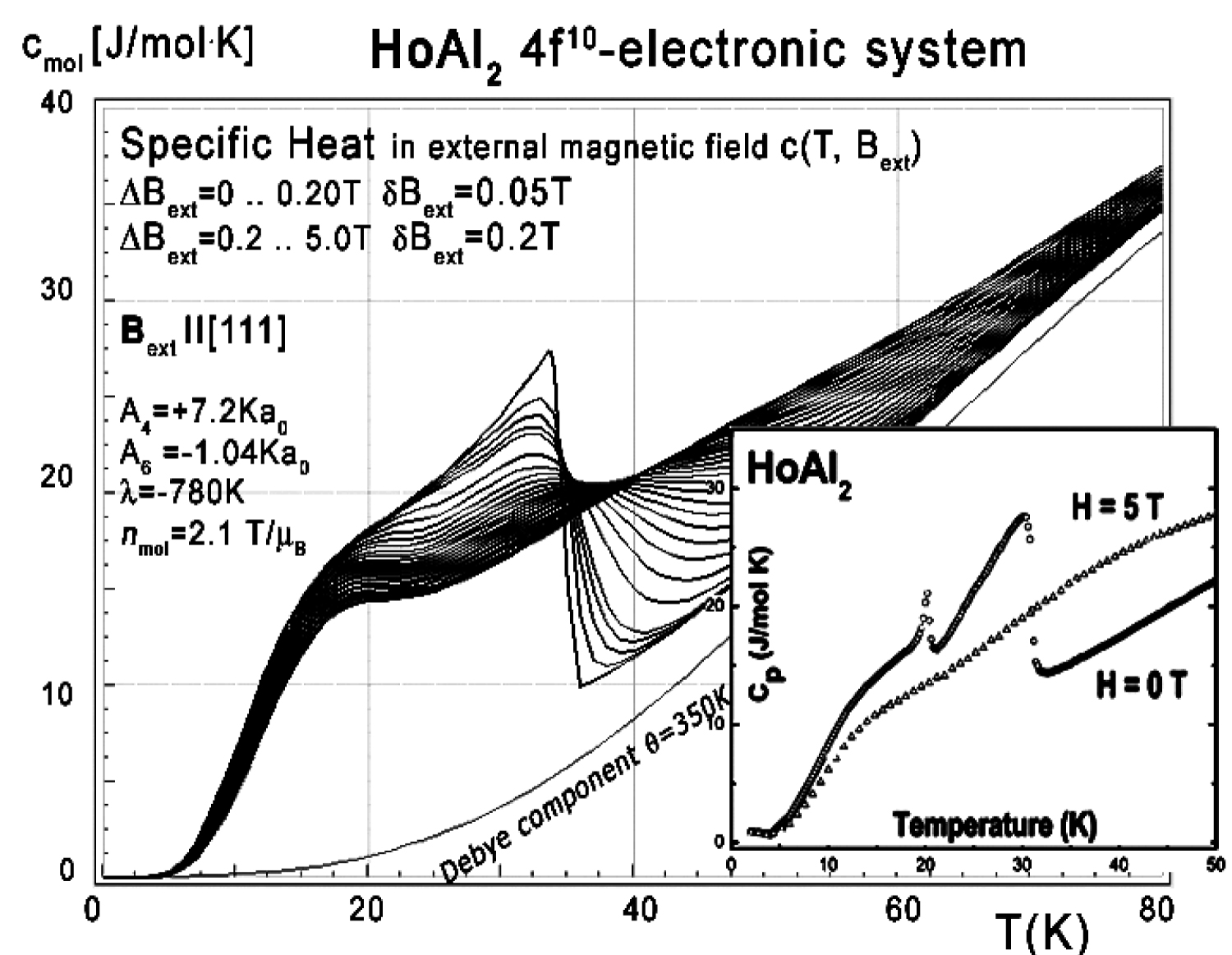
Figure 21: Calculated 4f10-electronic system...
Calculated 4f10-electronic system component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature for Ho ions in HoAl2 under the influence of an external magnetic field applied along the [100] direction. Inset: Experimental data from [7].
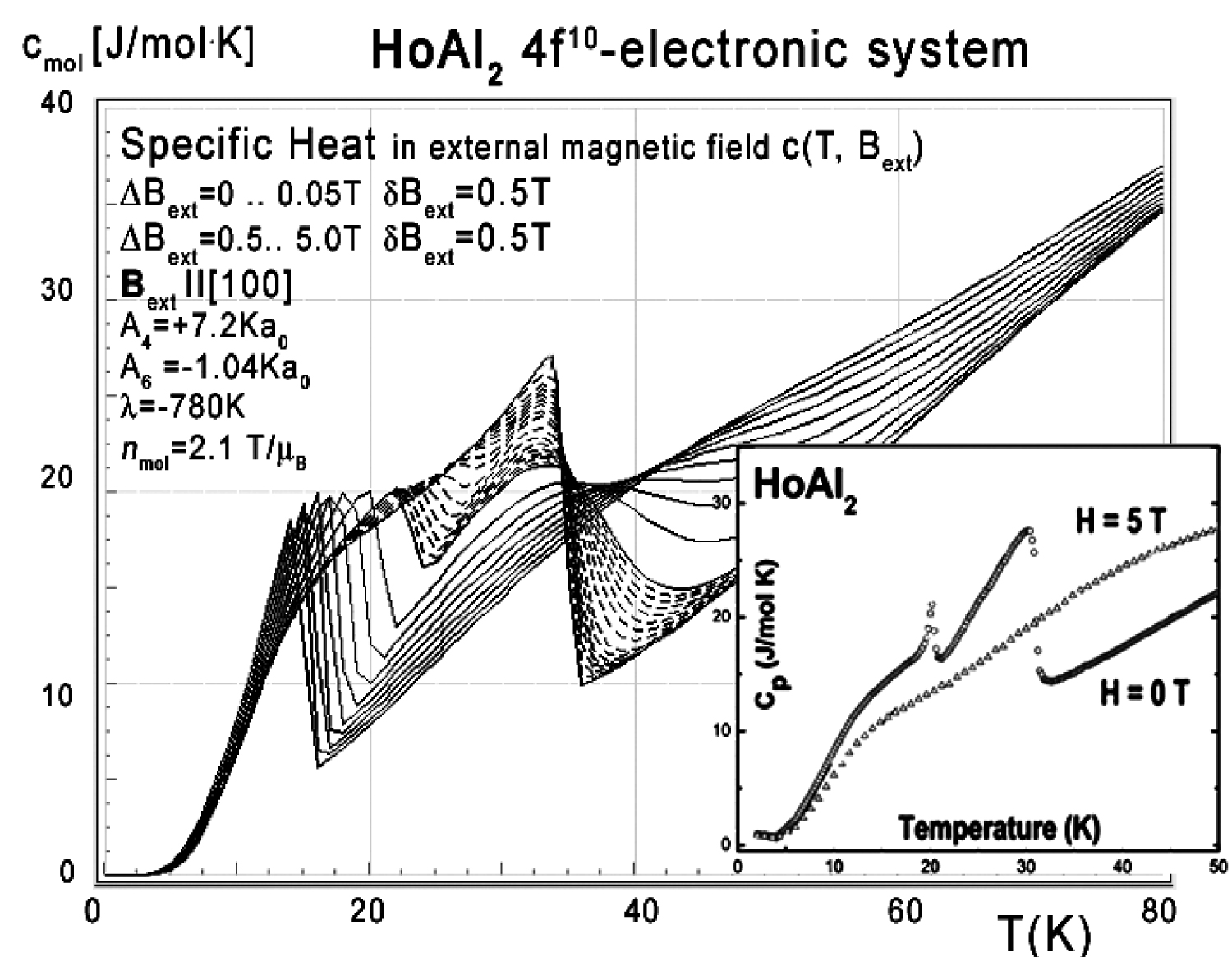
Figure 22: Calculated molar specific heat...
Calculated molar specific heat (14) vs. temperature for Ho ions in HoAl2 under the influence of an external magnetic field applied along the [100] direction. Inset: Experimental data from [7].

Figure 23: Calculated molar specific heat...
Calculated molar specific heat (14) vs. temperature for Ho ions in HoAl2 under the influence of an external magnetic field applied along easy magnetization axis in the [110] direction. Inset: Experimental data from [7].
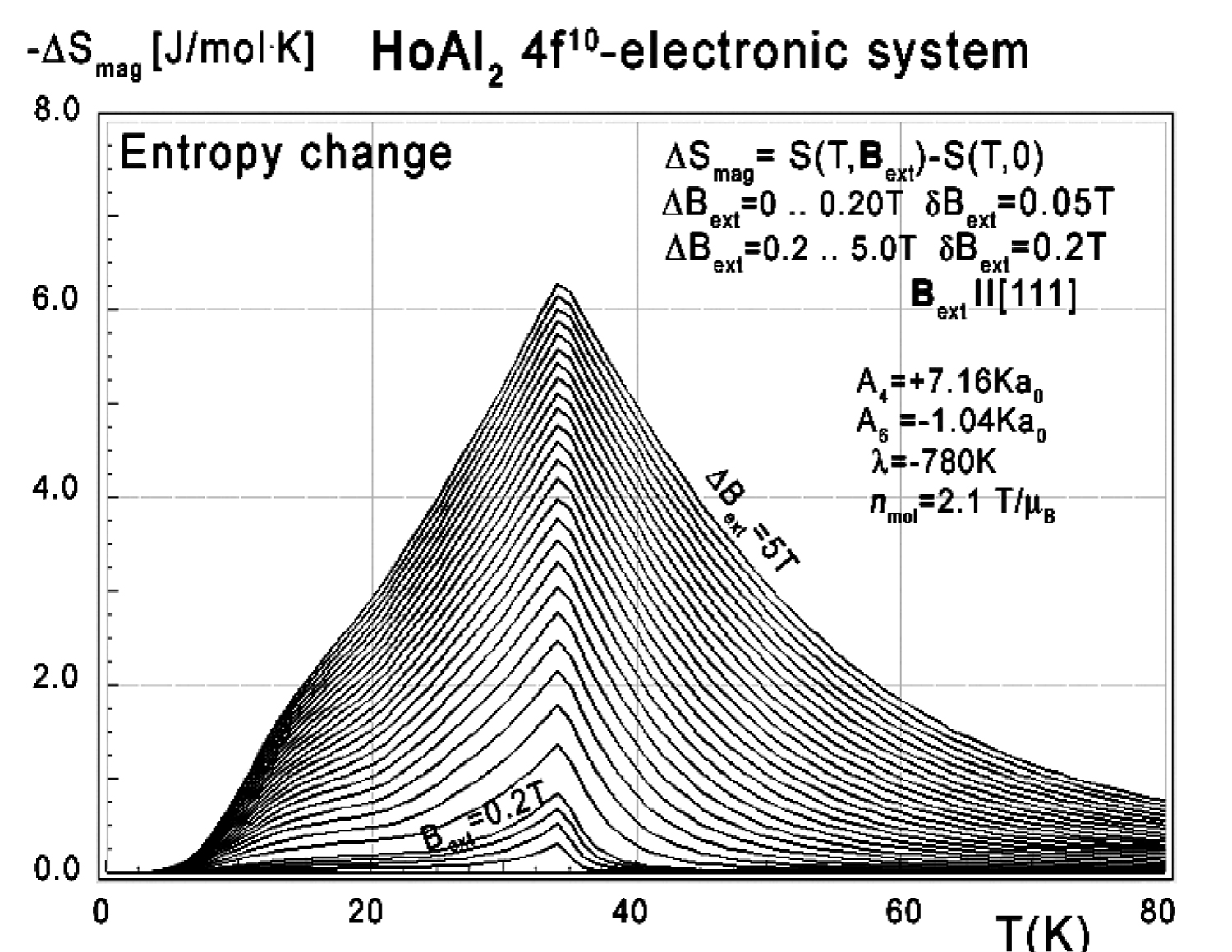
Figure 24: Calculated isothermal entropy change...
Calculated isothermal entropy change of 4f10-electronic system vs. temperature (16) of Ho3+ ions in HoAl2 under the influence of various external magnetic field values from 0 to 0.2 T with step 0.05 T and from 0 to 0.2 to 5.0 T with step 0.2 T applied along the [111] direction.
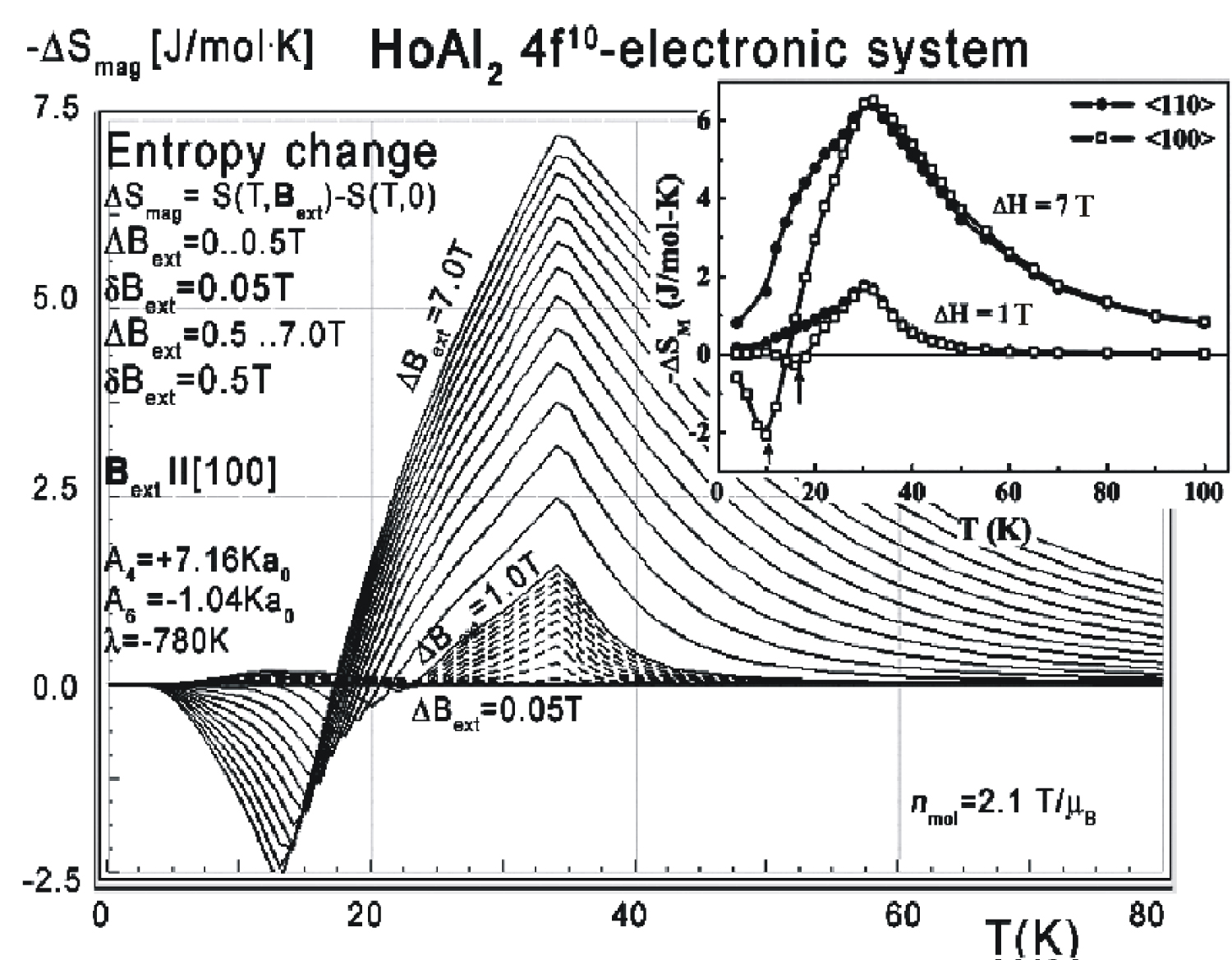
Figure 25: Calculated isothermal entropy change of...
Calculated isothermal entropy change of 4f10-electronic system vs. temperature (16) of Ho ions in HoAl2 under the influence of various external magnetic field values from 0 to 0.5 T with step 0.05 T and from 0 to 0.5 to 7.0 T with step 0.5 T applied along the [100] direction. Inset: experimental data from [8].
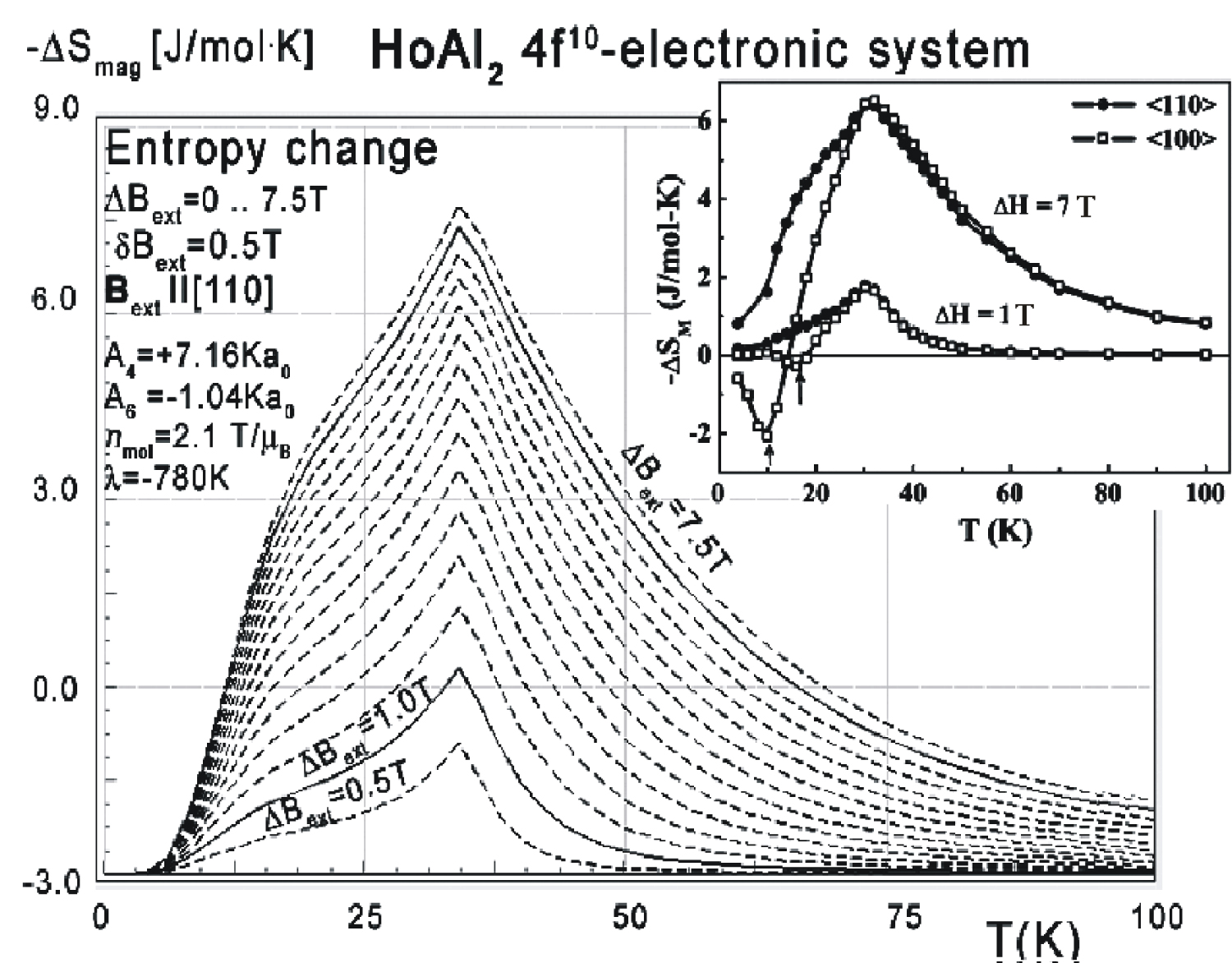
Figure 26: Calculated isothermal entropy change...
Calculated isothermal entropy change of 4f10-electronic system vs. temperature (16) of Ho3+ ions in HoAl2 under the influence of various external magnetic field values from 0 to 7.5 T with step 0.5 T applied along the [111] direction. Inset: Experimental data from [8].
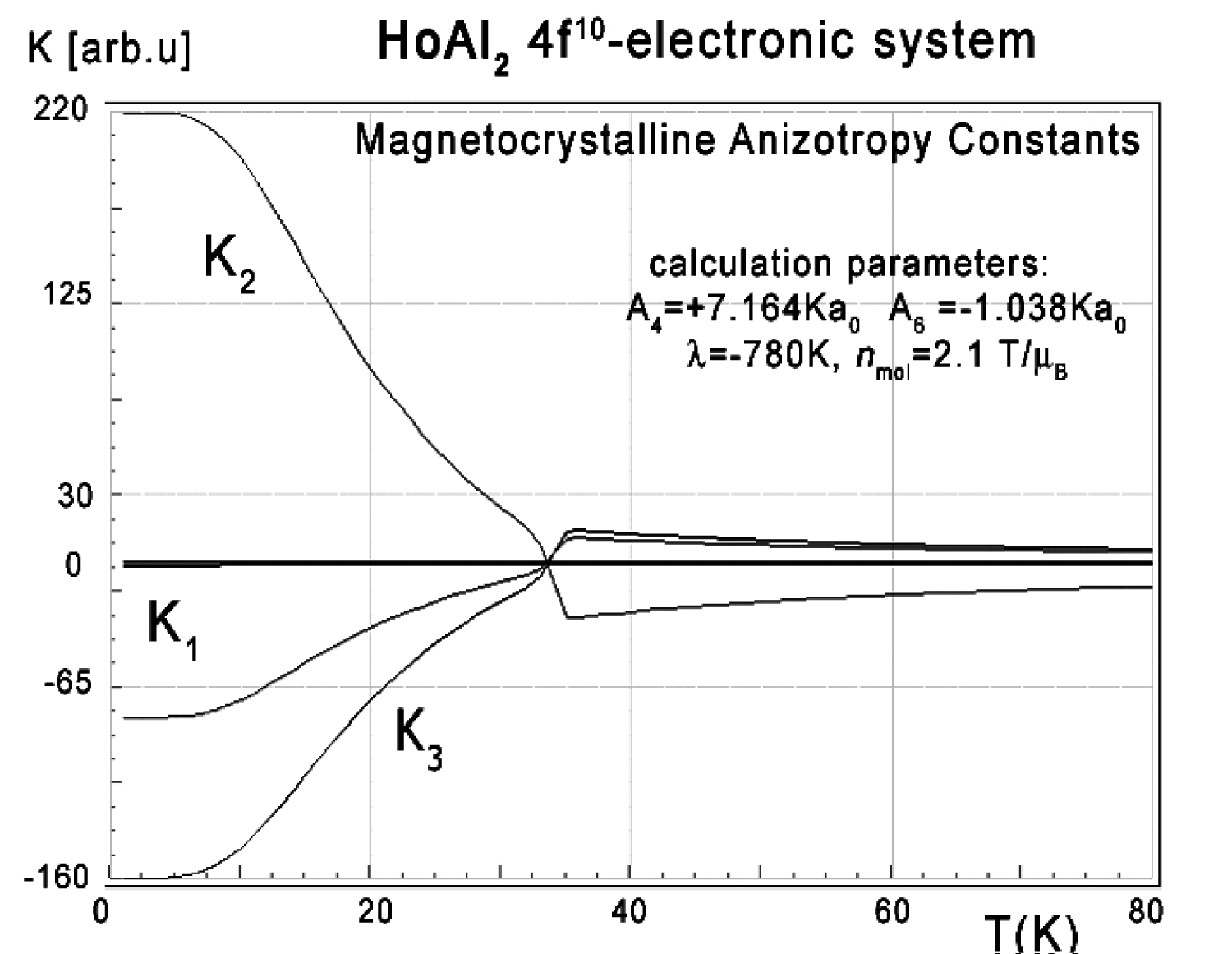
Figure 27: Magnetocrystalline anisotropy...
Magnetocrystalline anisotropy constants K1, K2 and K3 vs. temperature for Ho3+ ions in HoAl2 in absence of external magnetic field according to (17).
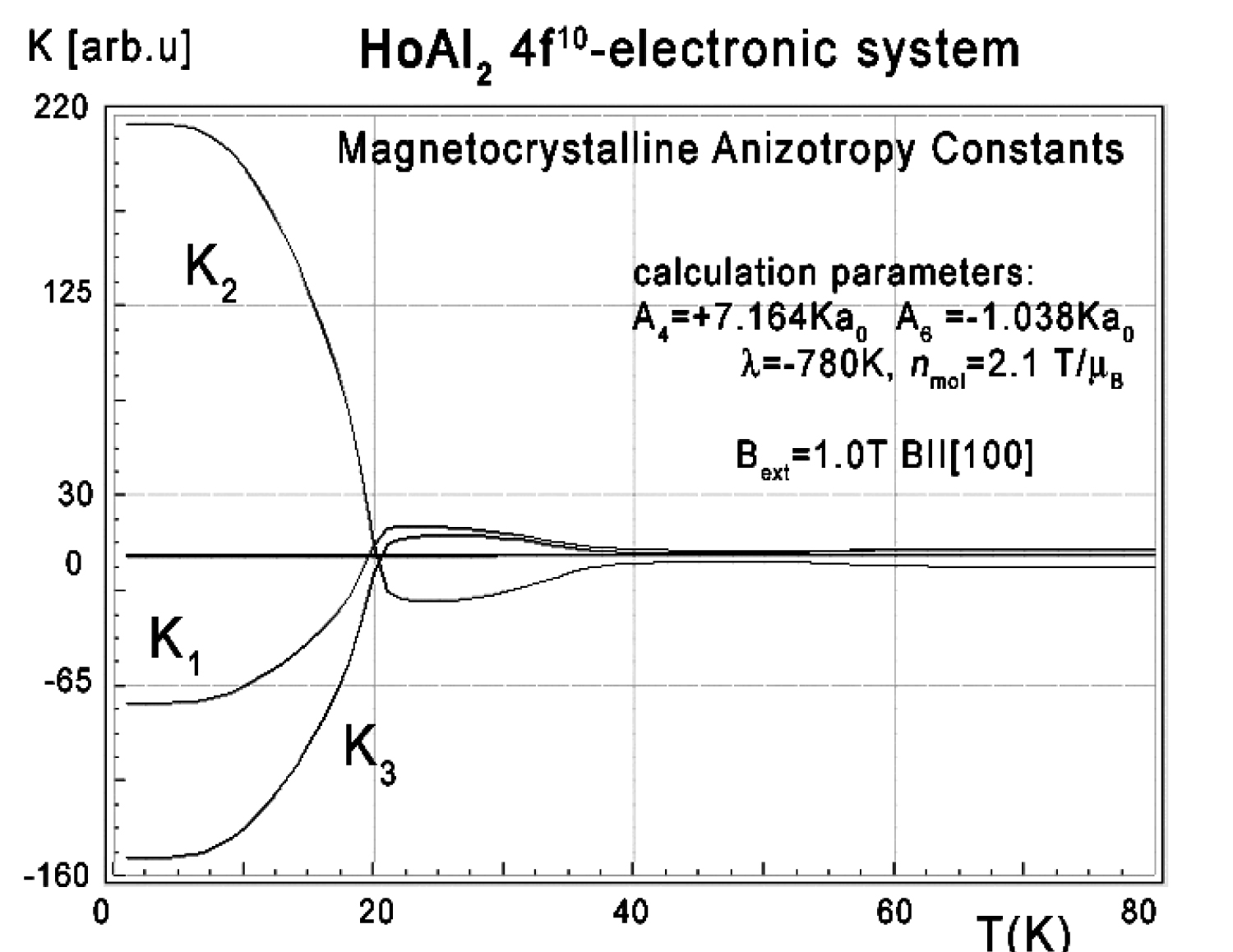
Figure 28: Magnetocrystalline anisotropy constants...
Magnetocrystalline anisotropy constants K1, K2 and K3 vs. temperature for Ho ions in HoAl2 under the influence of CEF and molecular magnetic field calculated according to (17).
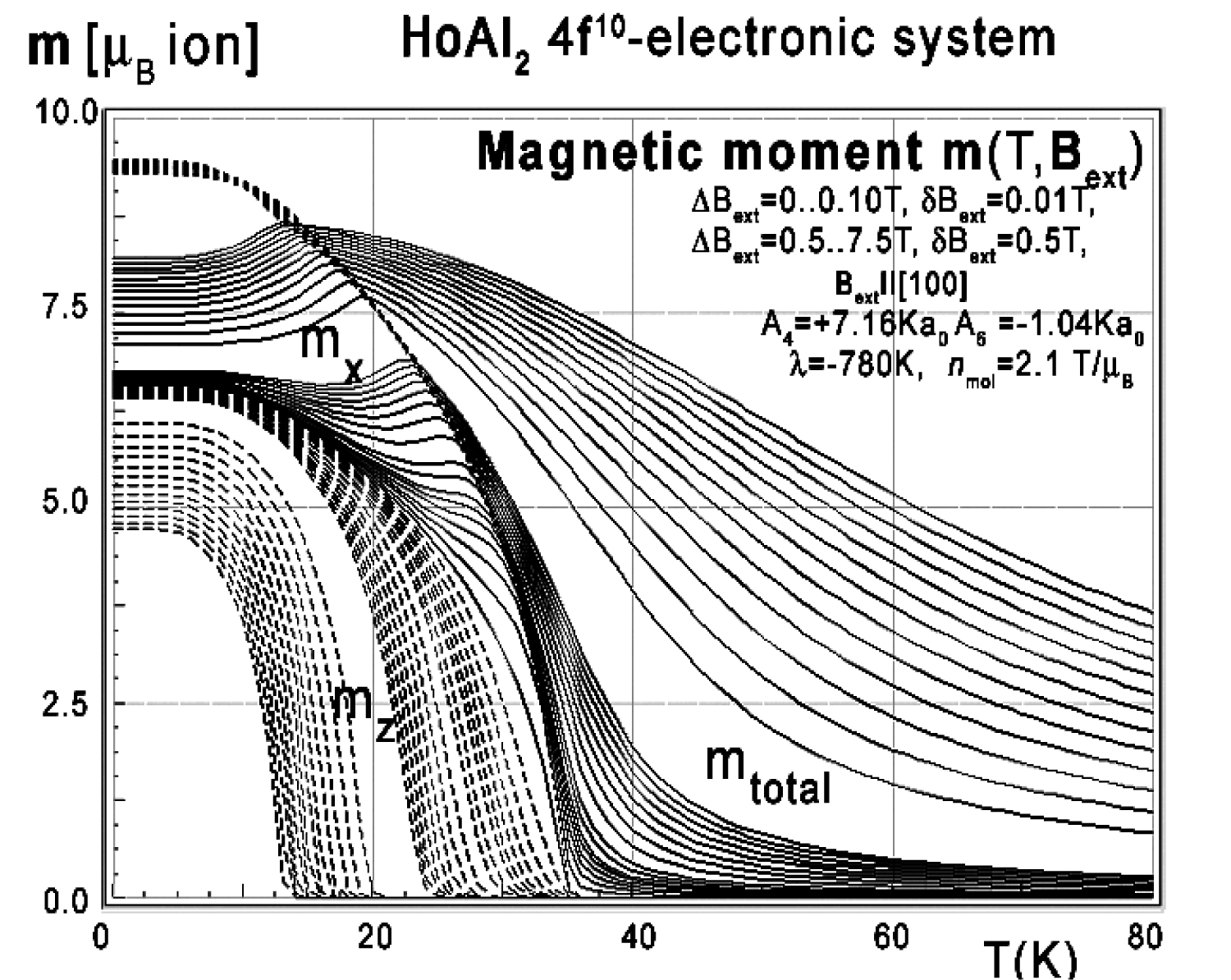
Figure 29: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment vs. temperature, calculated for Ho ions in HoAl2 under the influence of various external magnetic field values from 0 to 0.1 T with step 0.01 T and from 0.5 to 7.5 T with step 0.5 T applied along the [100] direction.
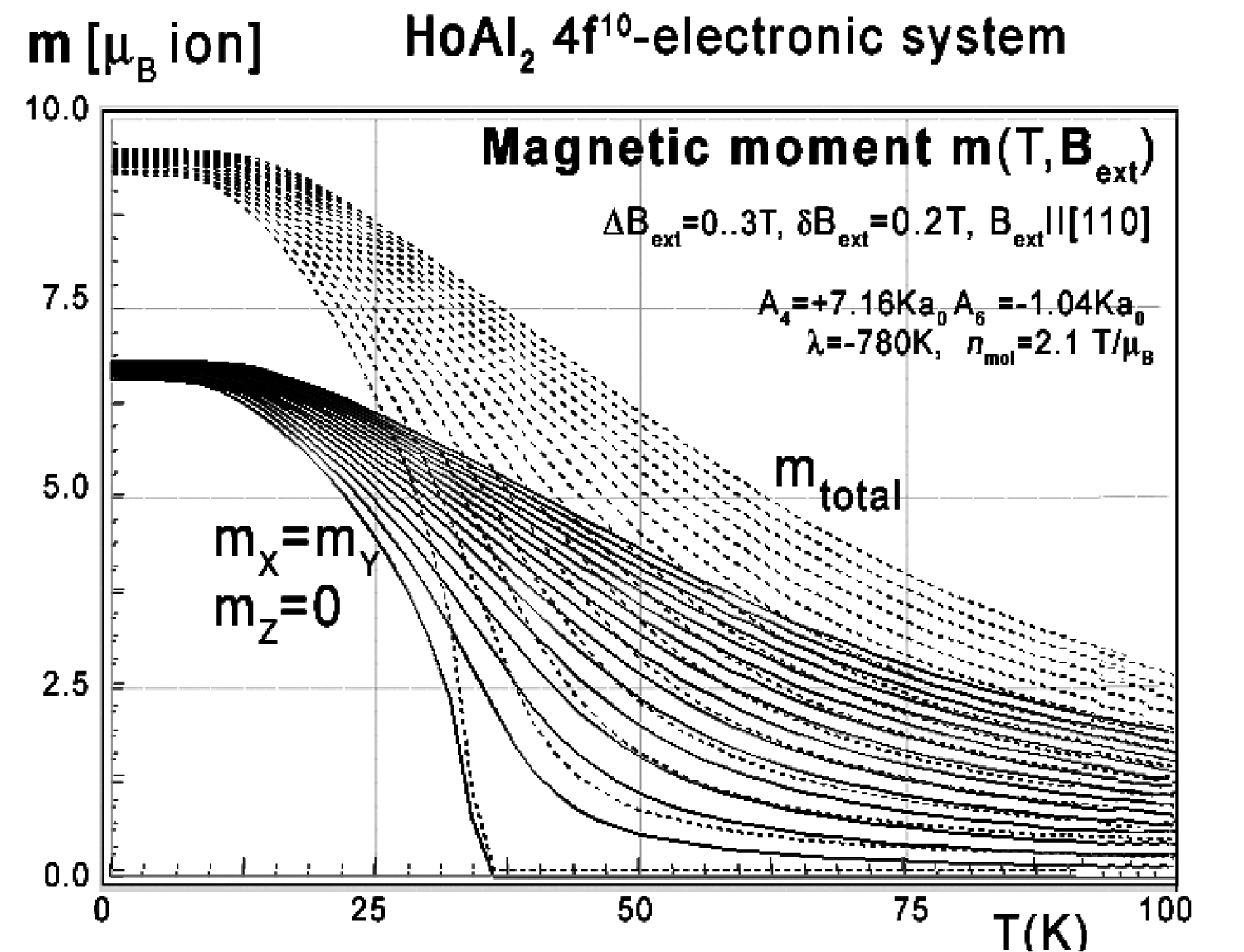
Figure 30: Calculated x-components (solid lines)...
Calculated x-components (solid lines), z-components (dashed lines) of total magnetic moment mtotal (dotted lines) vs. temperature, calculated for Ho ions in HoAl2 under the influence of CEF, molecular magnetic field and various values of external magnetic field from 0 to 3 T with step 0.2 T applied along the [110] direction.

Figure 31: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment vs. temperature, calculated for Ho ions in HoAl2 under the influence of CEF and molecular magnetic field and various values of external magnetic field from 0 to 0.2 T with step 0.05 T and from 0.2 to 5.0 T with step 0.2 T applied along the [111] direction.
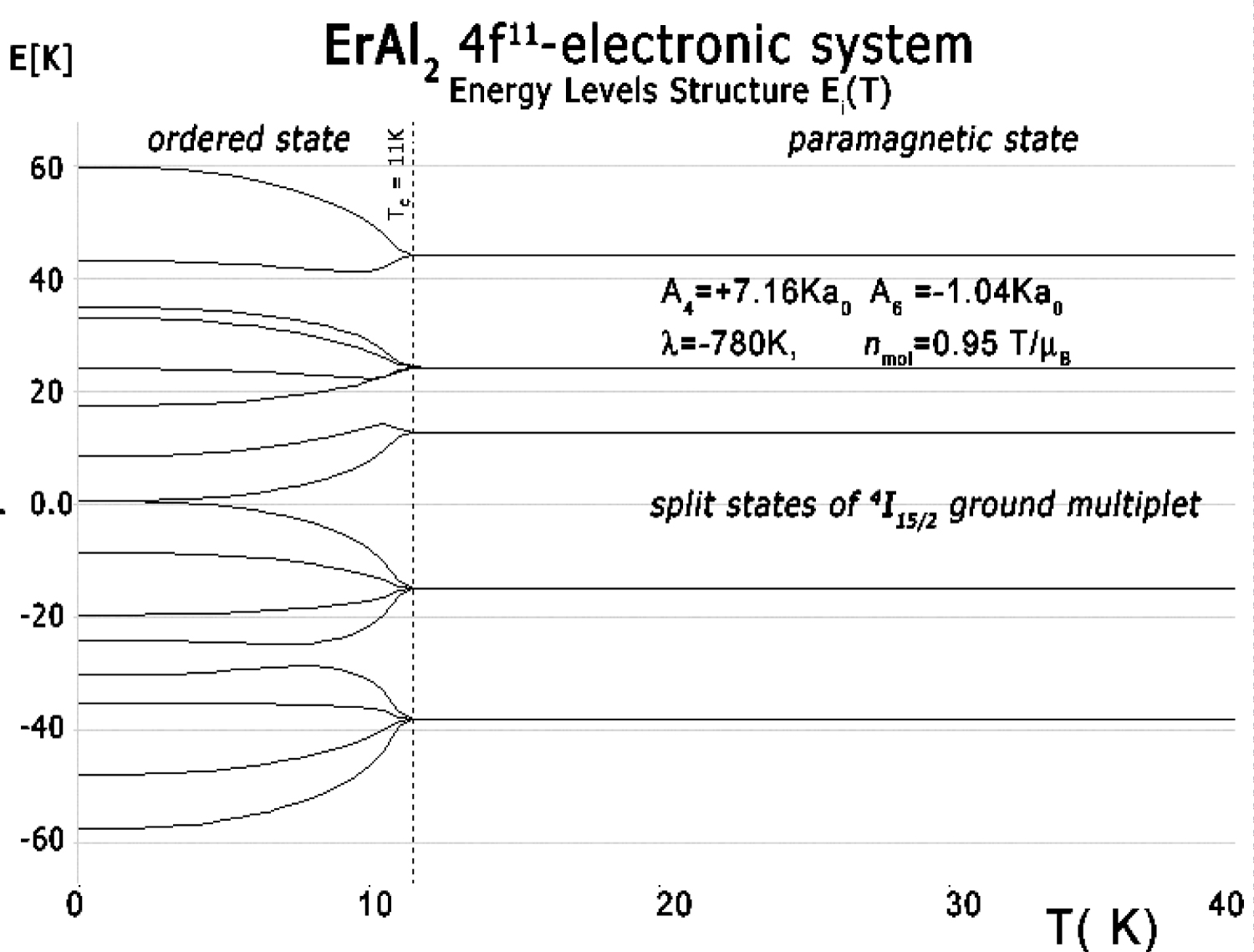
Figure 32: The result of calculation of energy...
The result of calculation of energy level positions vs. temperature of the fine electronic structure of 4f11 electronic configuration of Er ions in ErAl2.
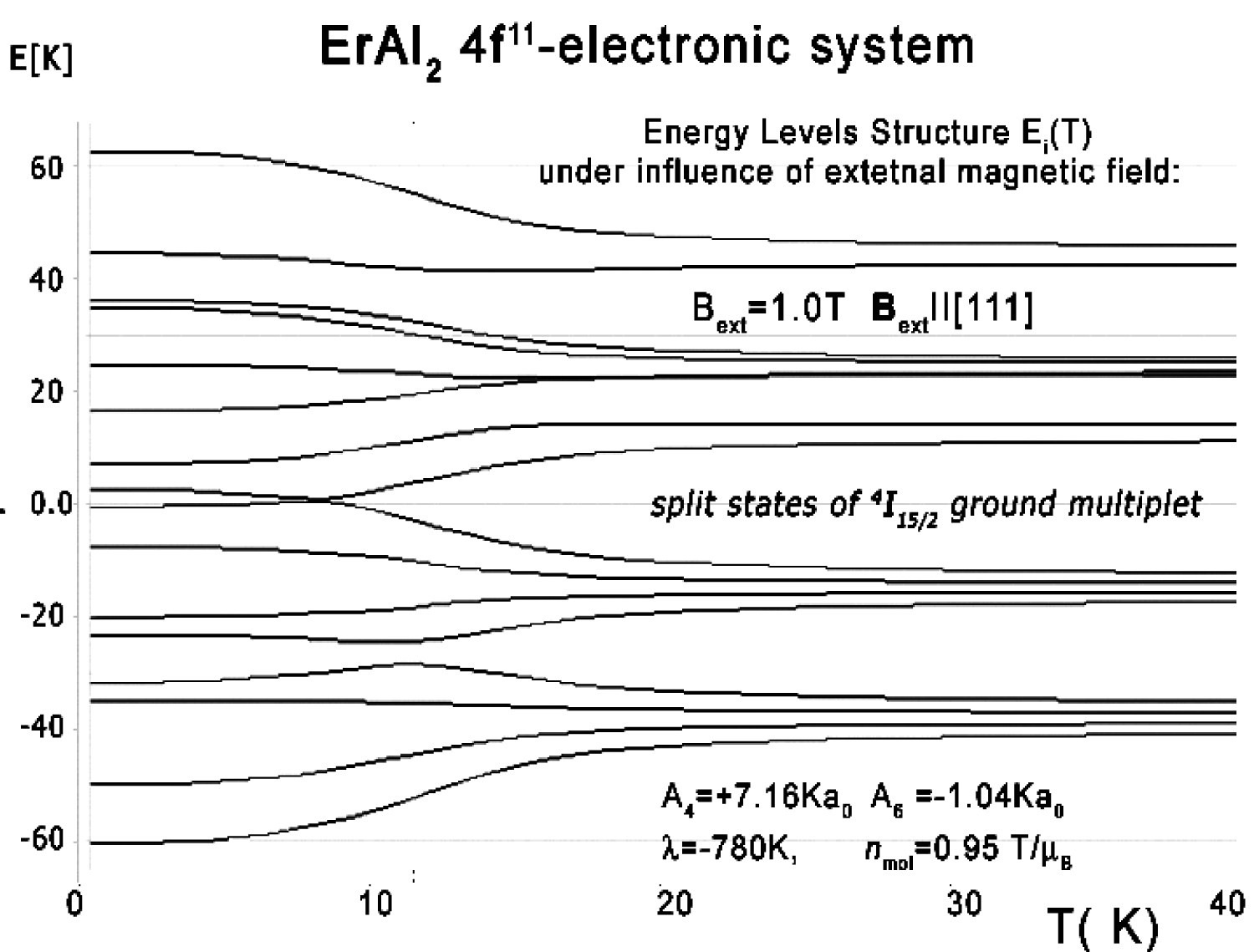
Figure 33: Calculated energy level structure of...
Calculated energy level structure of 4f11 electronic system of Er ions vs. temperature under the influence of external magnetic field Bext = 1 T applied along the [111] direction.
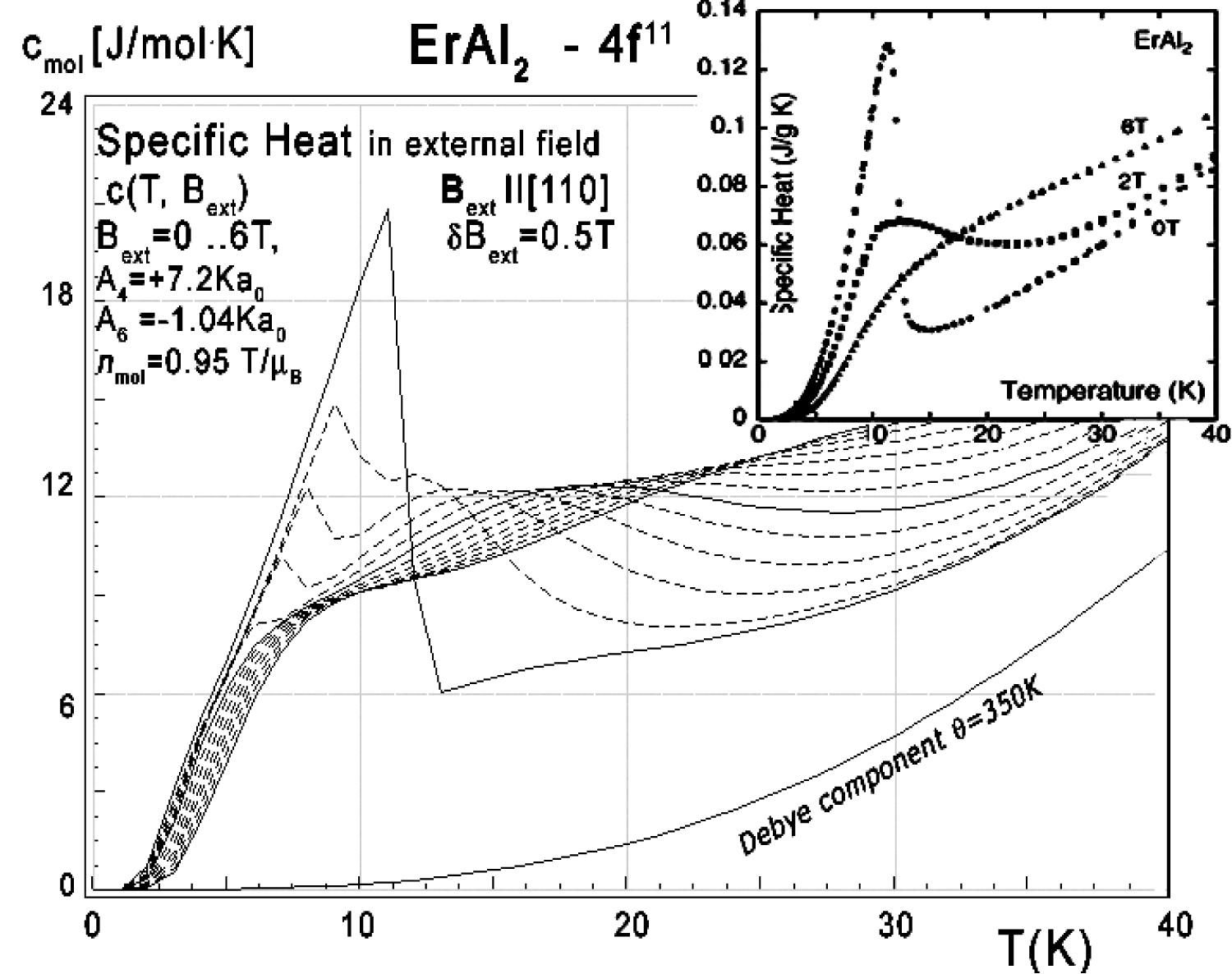
Figure 34: Calculated 4f11-electronic system...
Calculated 4f11-electronic system component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature of Er ions in ErAl2 under the influence of external magnetic field from 0 to 6 T with step 0.5 T applied along the [110] direction. Inset: experimental data from [11] congruent with results calculated for Bext = 0, Bext = 2.0 T and Bext = 6.0 T lines are solid lines.
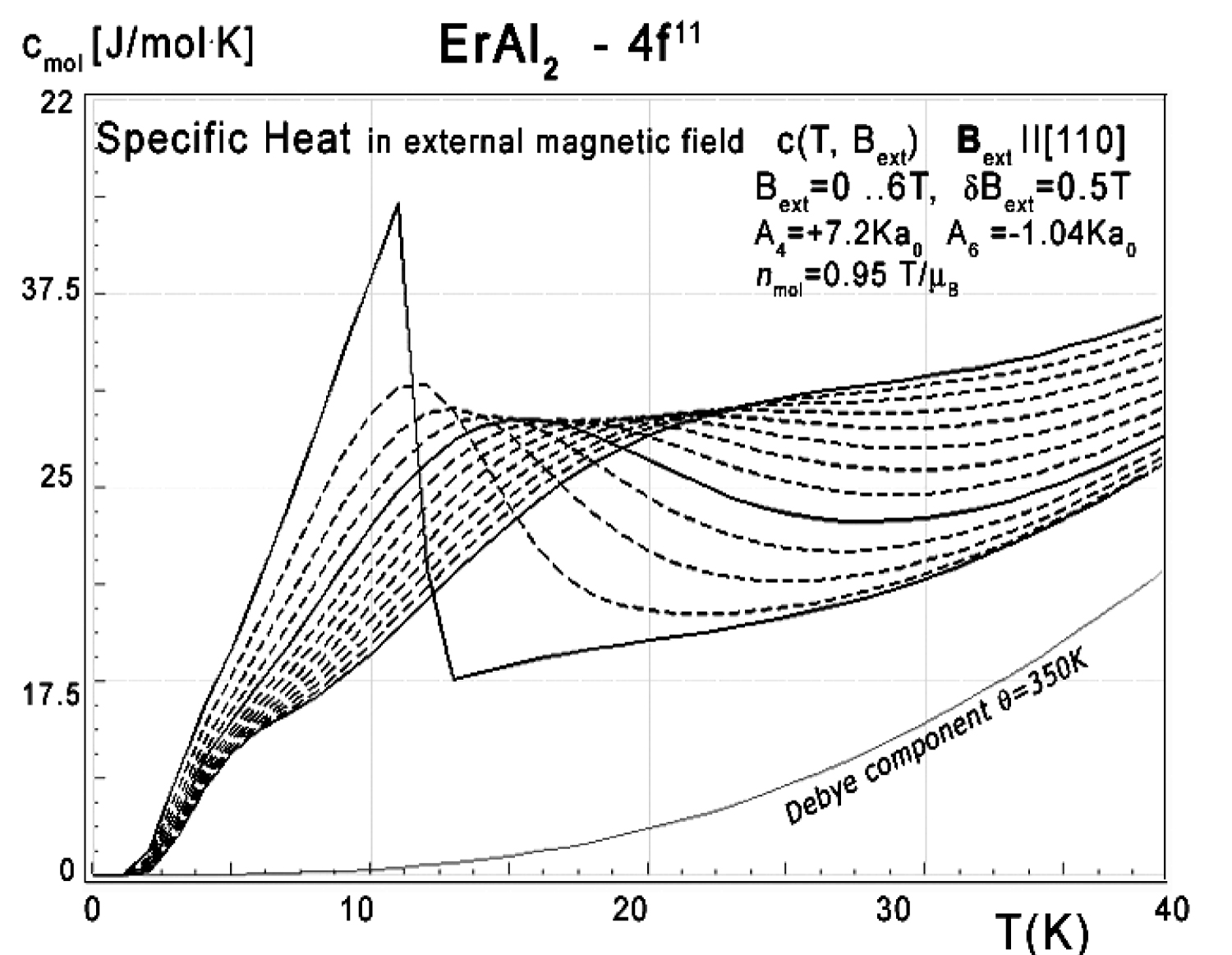
Figure 35: Calculated 4f11-electronic system component...
Calculated 4f11-electronic system component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature of Er ions in ErAl2 under the influence of external magnetic field from 0 to 6 T with step 0.5 T applied along the [110] direction.
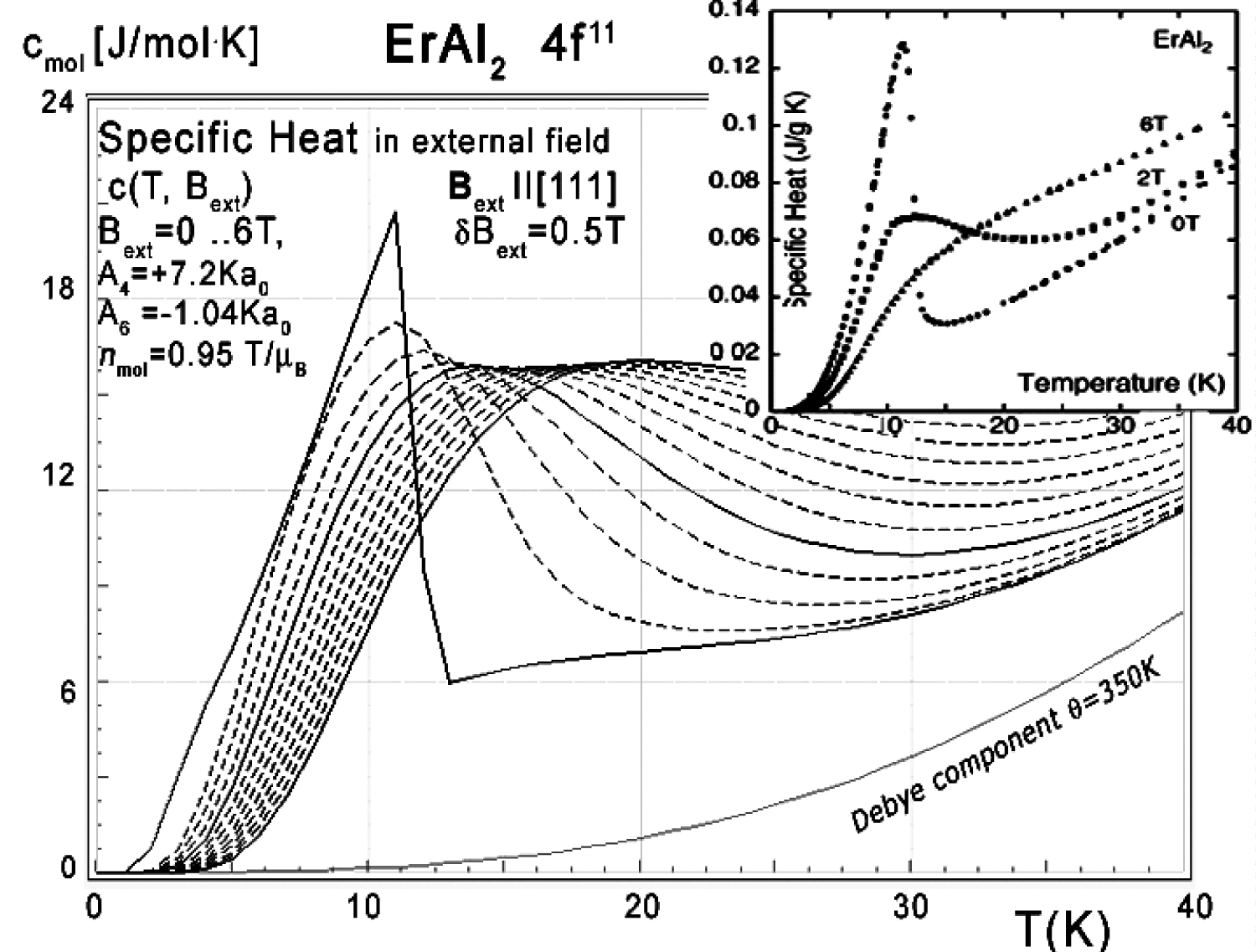
Figure 36: Calculated 4f11-electronic system...
Calculated 4f11-electronic system component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature of Er ions in ErAl2 under the influence of external magnetic field from 0 to 6 T with step 0.5 T applied along the [111] direction. Inset: experimental data from [11] congruent with results calculated for Bext = 0, Bext = 2.0 T and Bext = 6.0 T lines are solid lines.

Figure 37: Calculated isothermal entropy change...
Calculated isothermal entropy change of 4f11-electronic system vs. temperature (16) of Er ions in ErAl2 under the influence of various values of external magnetic field from 0 to 6 T with step 0.2 T applied along the [100] direction.
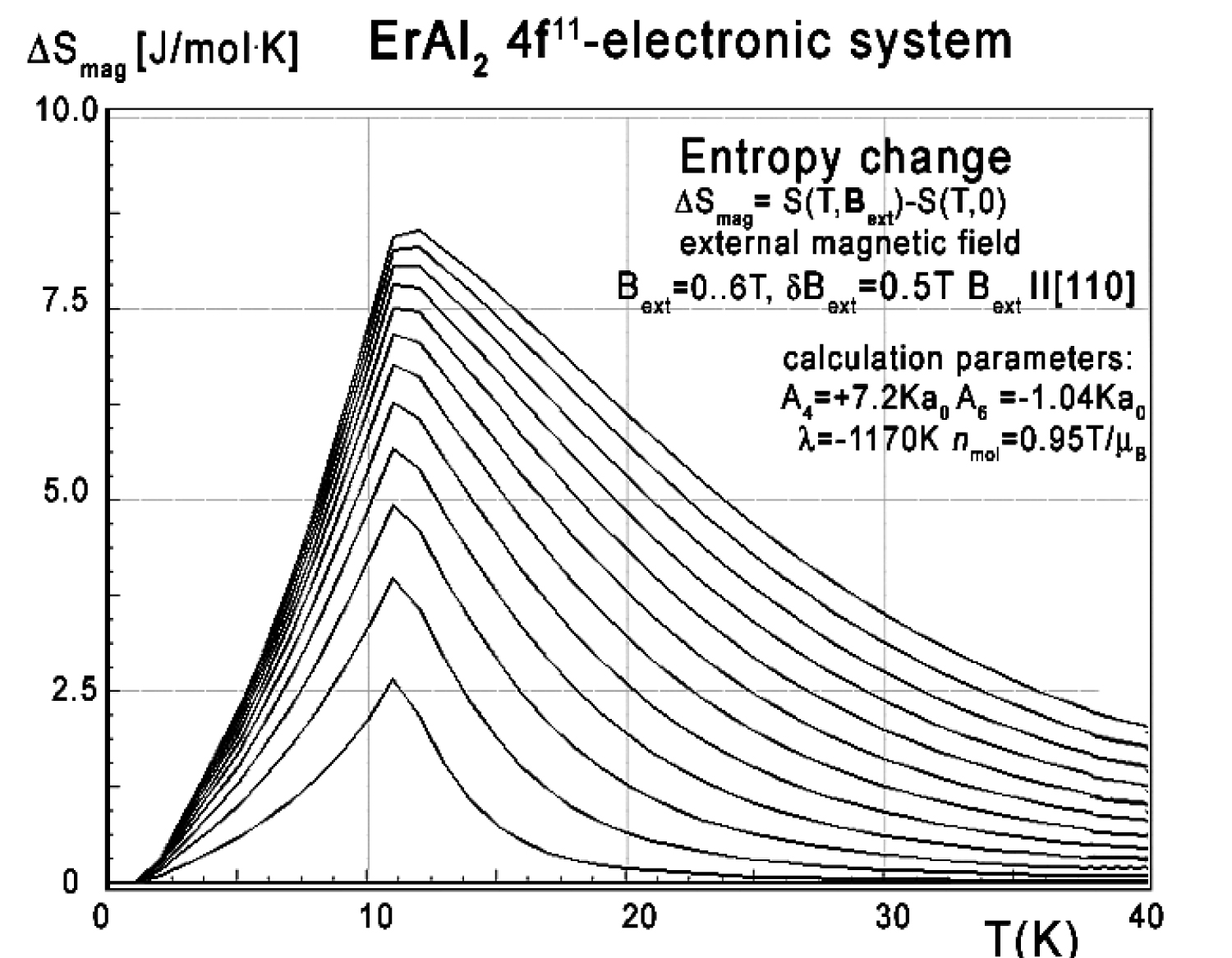
Figure 38: Calculated isothermal entropy change...
Calculated isothermal entropy change vs. temperature (16) for various values of external magnetic field from 0 to 6.0 T with step 0.5 T, applied along the [110] direction of ErAl2 crystal lattice.
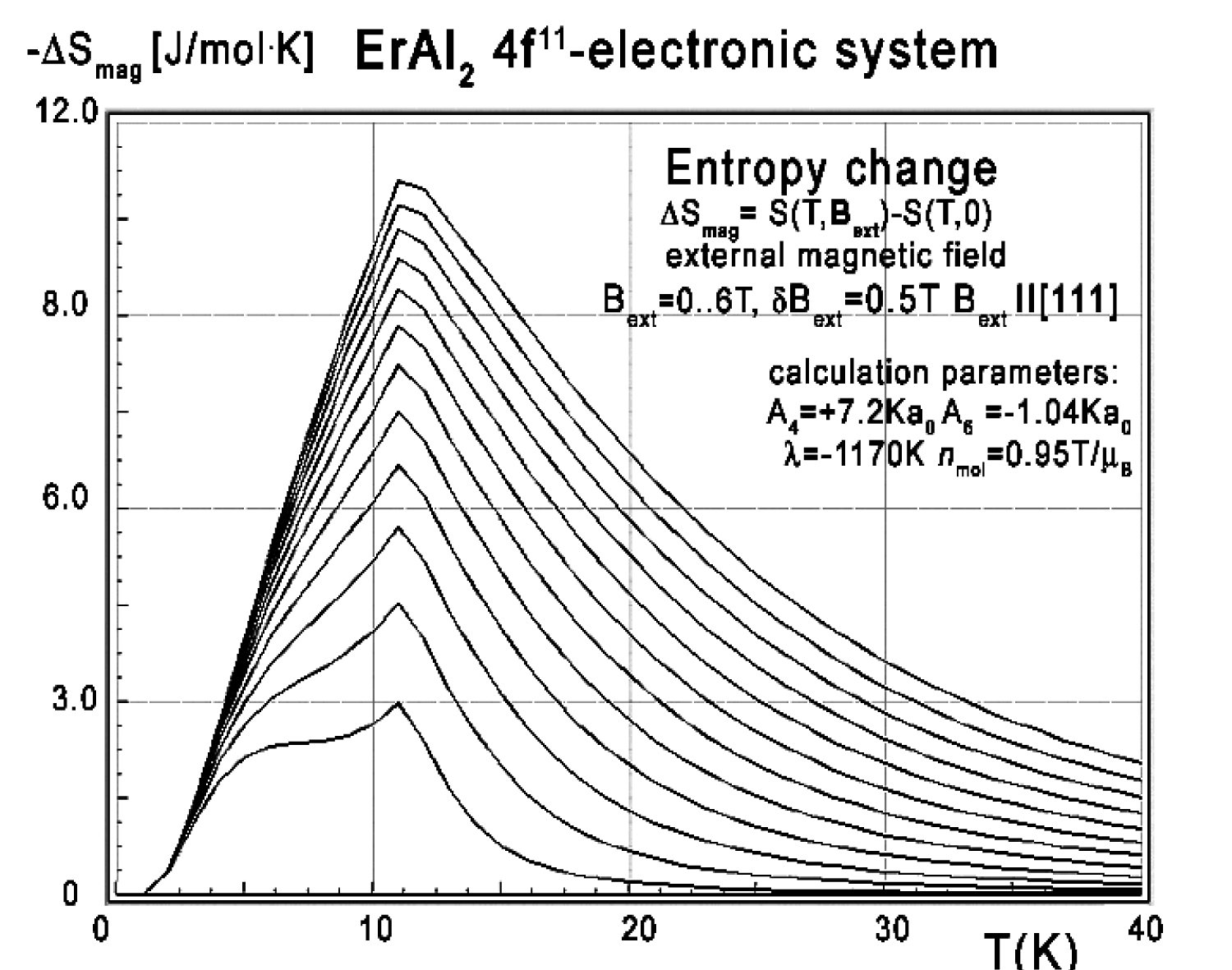
Figure 39: Calculated isothermal entropy change...
Calculated isothermal entropy change of ErAl2 vs. temperature (16) for various values of external magnetic field from 0 to 6 T with step 0.5 T applied along the diagonal [111] direction.
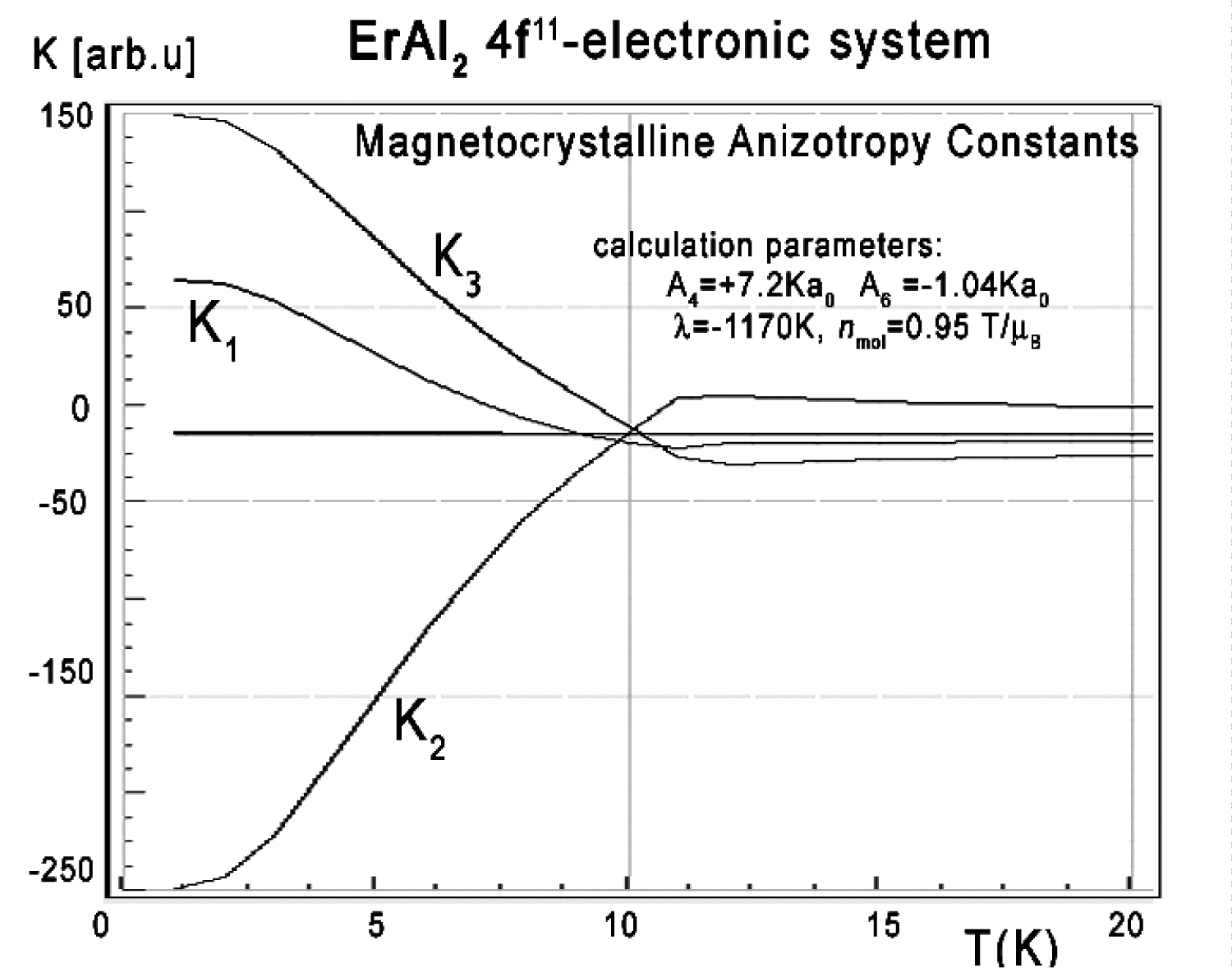
Figure 40: Calculated magnetocrystalline anisotropy...
Calculated magnetocrystalline anisotropy constants K1, K2 and K3 vs. temperature (17), calculated for Er ions under the influence of CEF established for RAl2 series and molecular magnetic field.
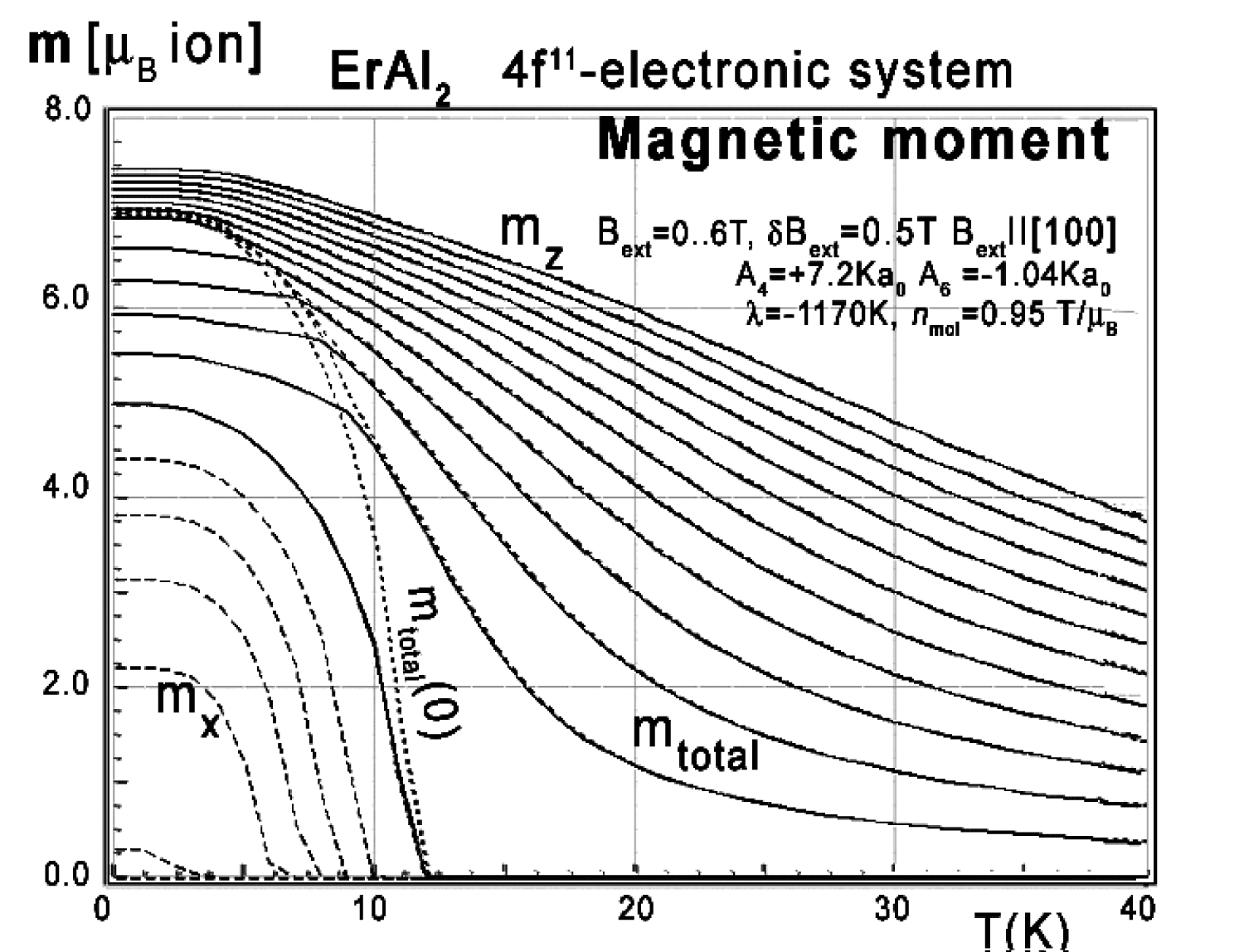
Figure 41: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment vs. temperature, calculated for Er ions in ErAl2 under the influence of CEF and molecular magnetic field and various values of external magnetic field from 0 to 6 T with step 0.5 T applied along the [100] direction.
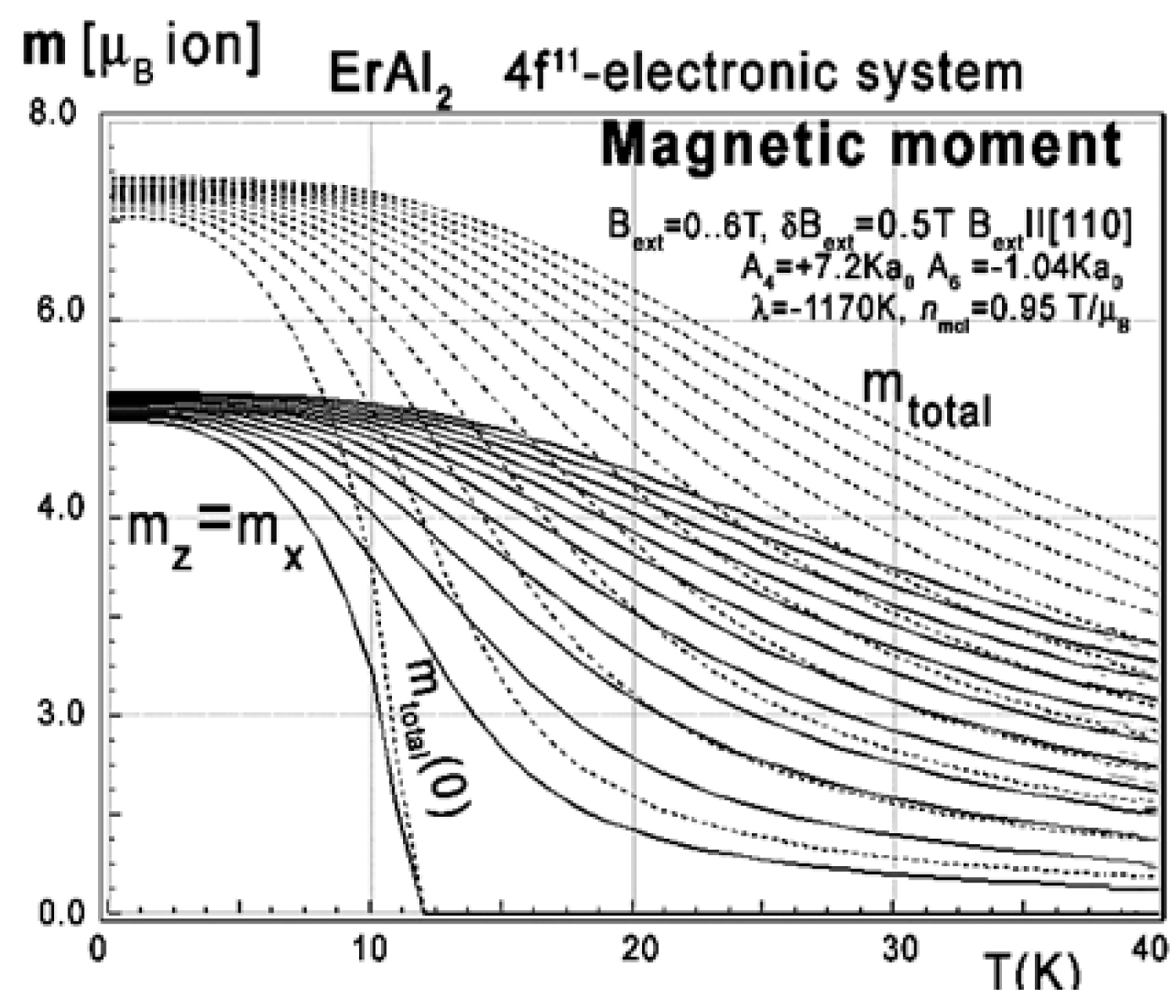
Figure 42: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment mtotal (dotted lines) vs. temperature, calculated for Er ions in ErAl2 under the influence of CEF, molecular magnetic field and various values of external magnetic field from 0 to 6 T with step 0.5 T applied along the [110] direction. my(T) = 0, x and z components of a magnetic moment are equally distributed.
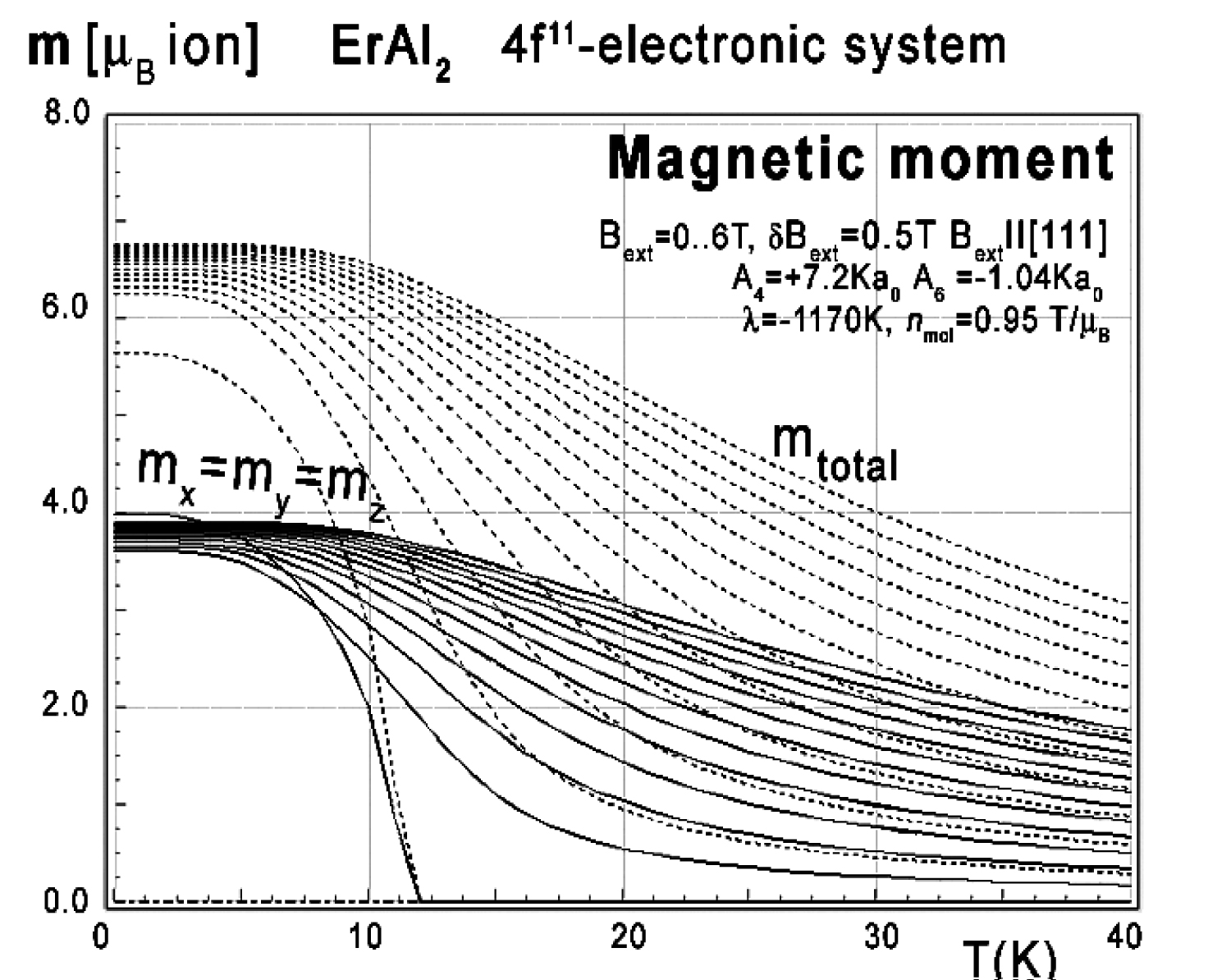
Figure 43: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of the total magnetic moment mtotal (dotted lines) vs. temperature, calculated for Er ions in ErAl2 under the influence of CEF, molecular magnetic field and various values of external magnetic field from 0 to 6 T with step 0.5 T applied along the [111] direction. All directional magnetic moment components are equally distributed.
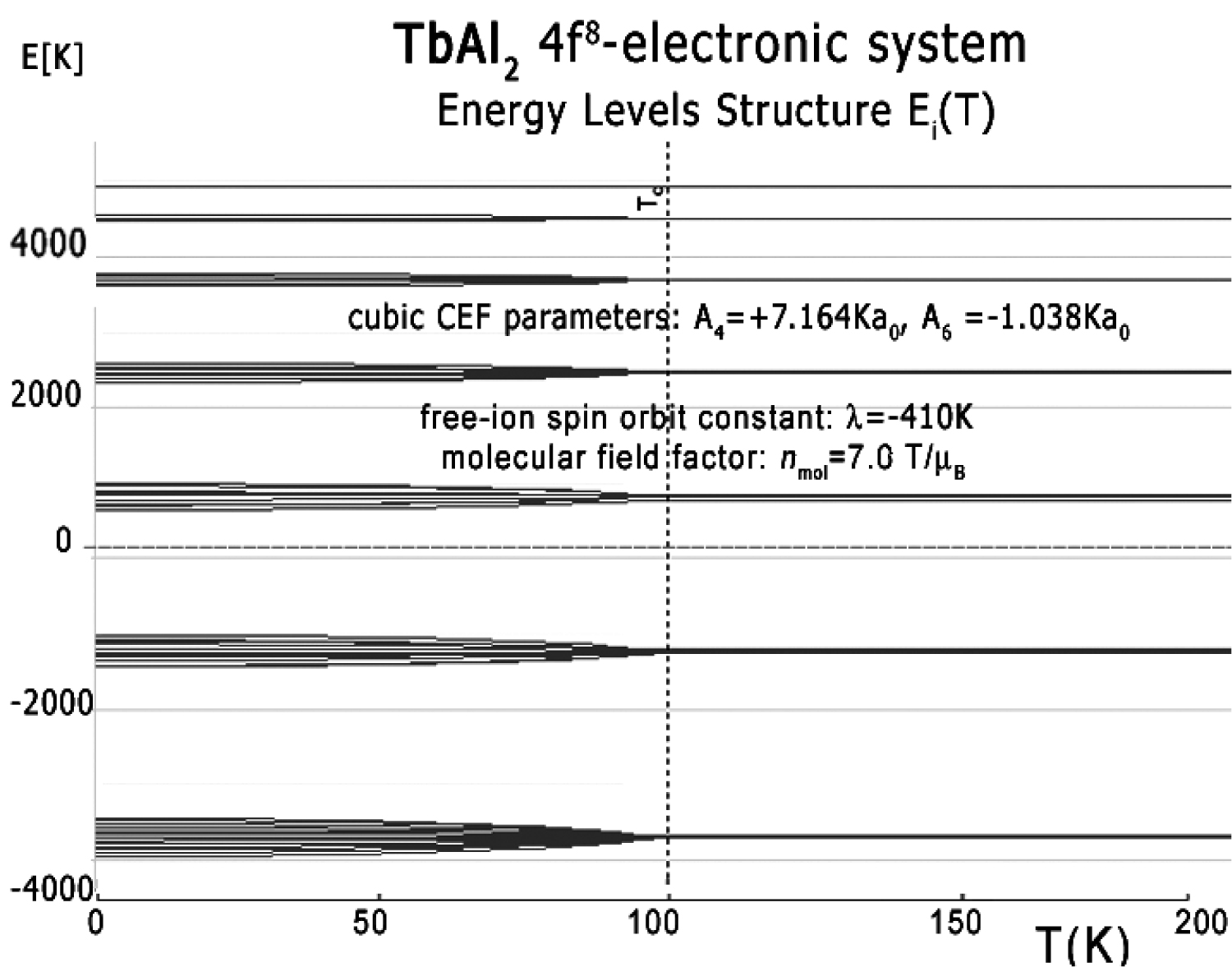
Figure 44: The result of calculation of energy...
The result of calculation of energy level positions vs. temperature of the fine electronic structure of 4f8 electronic configuration of Tb ions in TbAl2 in |L,S,Lz,Sz> space under the influence of intra-atomic spin-orbit coupling, inter-atomic self-consistent molecular magnetic field and Crystal Electric Field (CEF).

Figure 45: Calculated 4f-electron component of molar...
Calculated 4f-electron component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature for Tb ions in TbAl2 a) Under the influence of an external magnetic field applied along [100] direction; b) Under the influence of an external magnetic field applied along [111] direction; c) Under the influence of an external magnetic field applied along [110] direction.
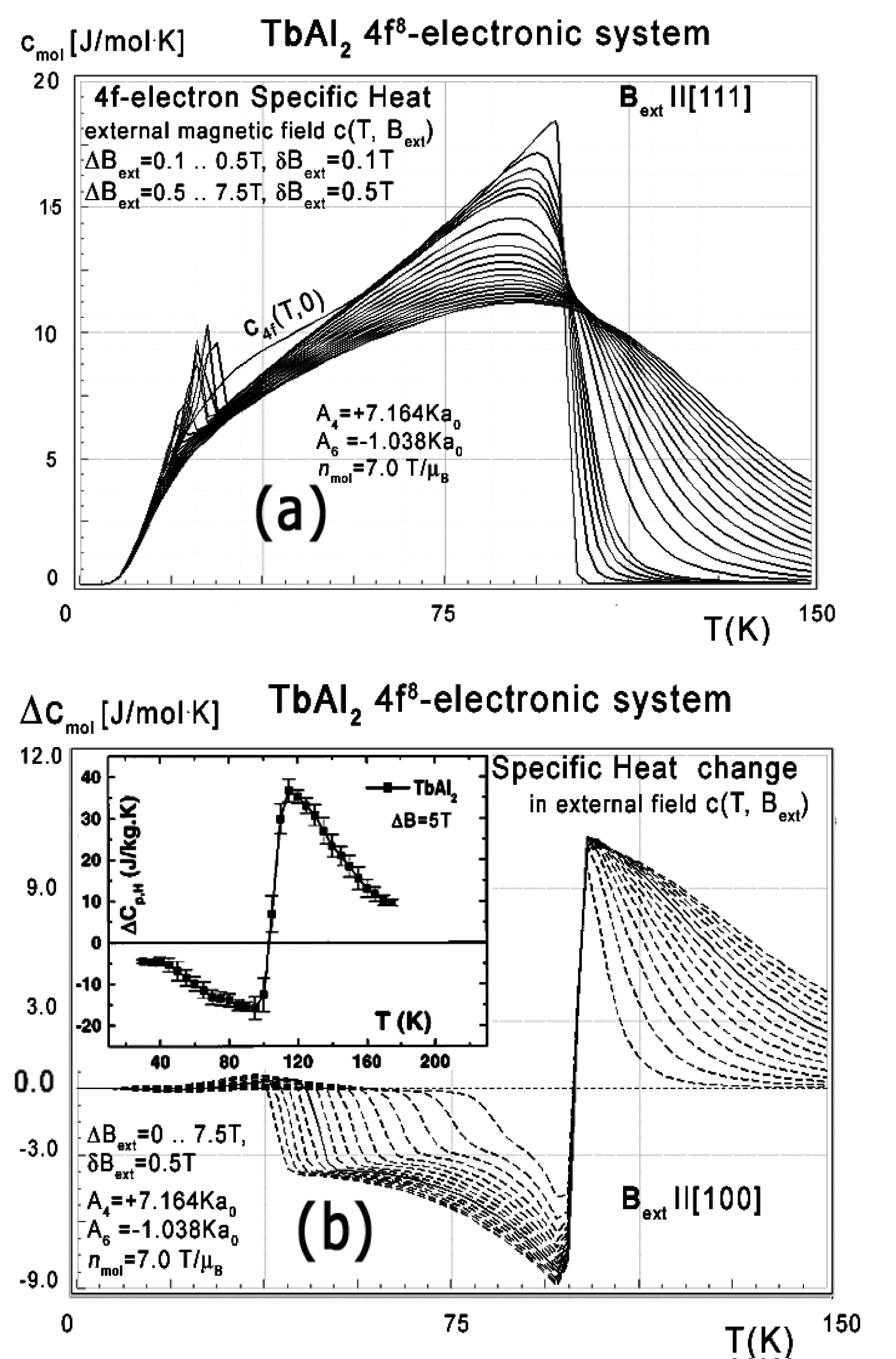
Figure 46: a) Calculated 4f-electron component...
a) Calculated 4f-electron component of molar specific heat vs. temperature for Tb ions in TbAl2 under the influence of an external magnetic field applied along [111] direction from 0 up to 7.5 T; b) Calculated specific heat change vs. temperature for Tb ions in TbAl2, under the influence of an external magnetic field applied along [100] direction from 0 to 7.5 T with step 0.5 T in comparison with experimental data from [9]. Solid line represents simulation for ΔBext = 0.5 T.

Figure 47: Calculated isothermal entropy change...
Calculated isothermal entropy change of 4f-electronic system vs. temperature (16) of Tb ions in TbAl2 under the influence of various external magnetic field values from 0 to 7.5 T with step 0.5 T a) Applied along [100] direction; b) Applied along [110] direction; c) Applied along [111] direction.
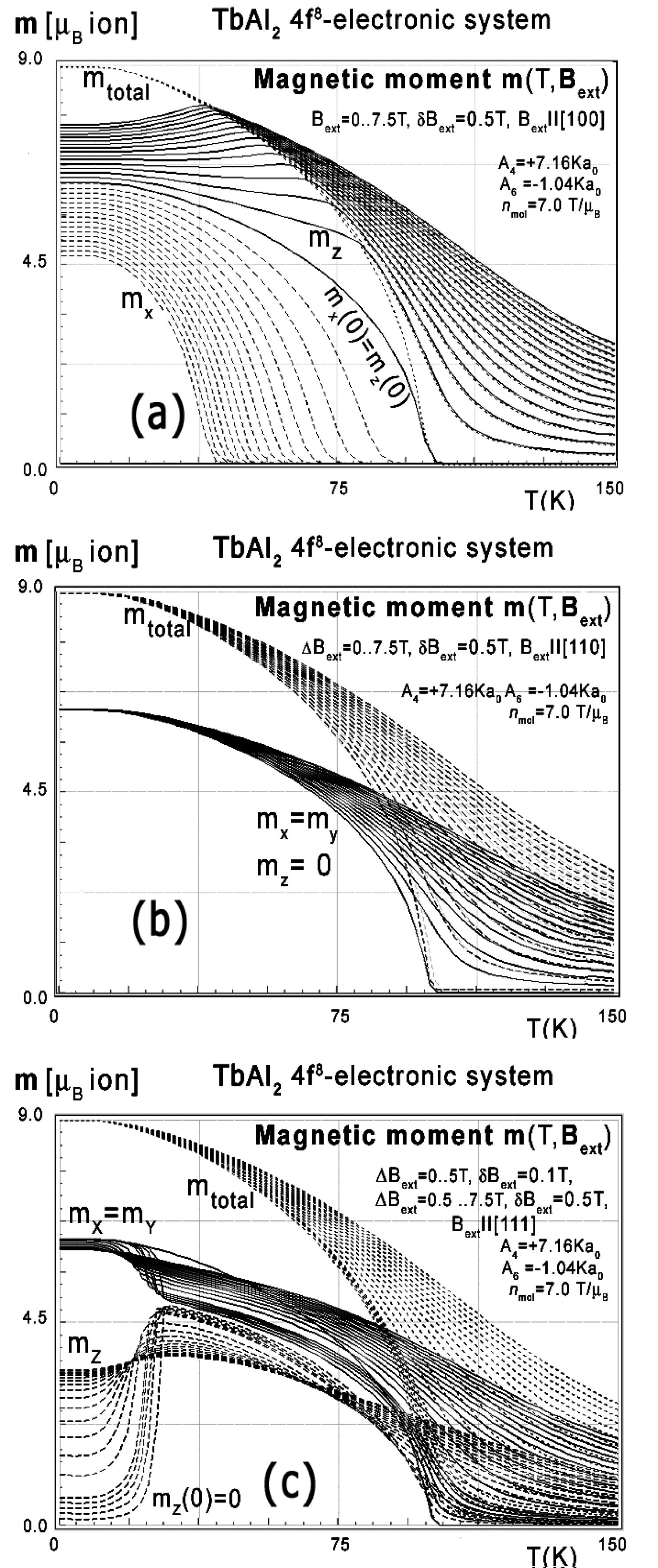
Figure 48: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment vs. temperature, calculated for Tb ions in TbAl2 under the influence of CEF and molecular magnetic field and various values of external magnetic field from 0 to 7.5 T with step 0.5 T a) Applied along [100] direction; b) Applied along [110] direction; c) Applied along [111] direction.

Figure 49: a) Energy level structure of Sm3+ ion...
a) Energy level structure of Sm3+ ion Ei(K) under the influence of defined CEF of SmAl2 calculated in |L,S,Lz,Sz> space. b) Lowest state of this structure, calculated under the influence of external magnetic field Bext = 2 T applied along [001]; c) Ground multiplet energy level structure vs. temperature calculated for 4f5 electronic system of Sm3+ in SmAl2 calculated in |J,Jz> space.
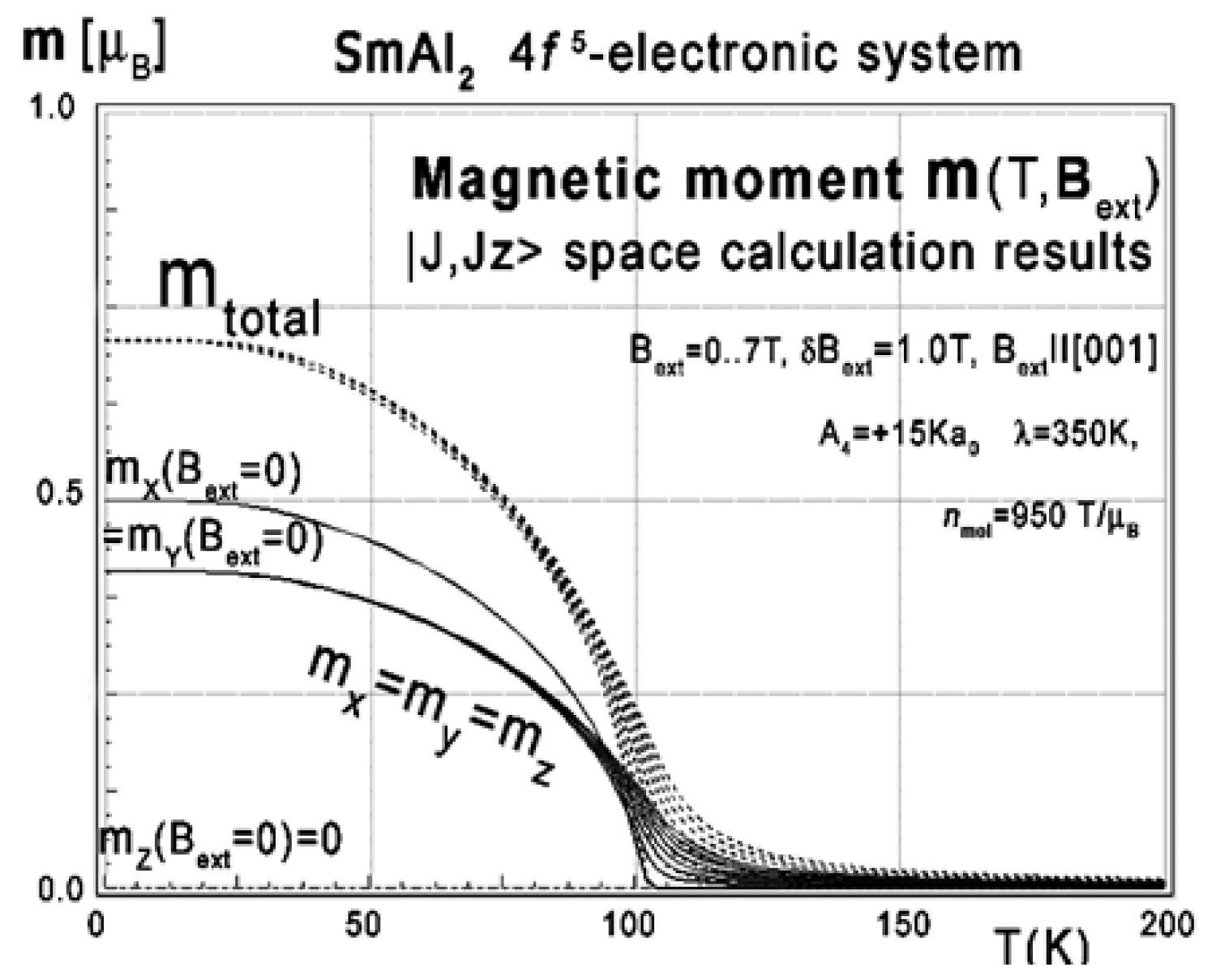
Figure 50: Calculated x,y,z-directional components...
Calculated x,y,z-directional components of total magnetic moment vs. temperature, calculated for 4f5 electronic system of Sm3+ in SmAl2 calculated in |J,Jz> space.
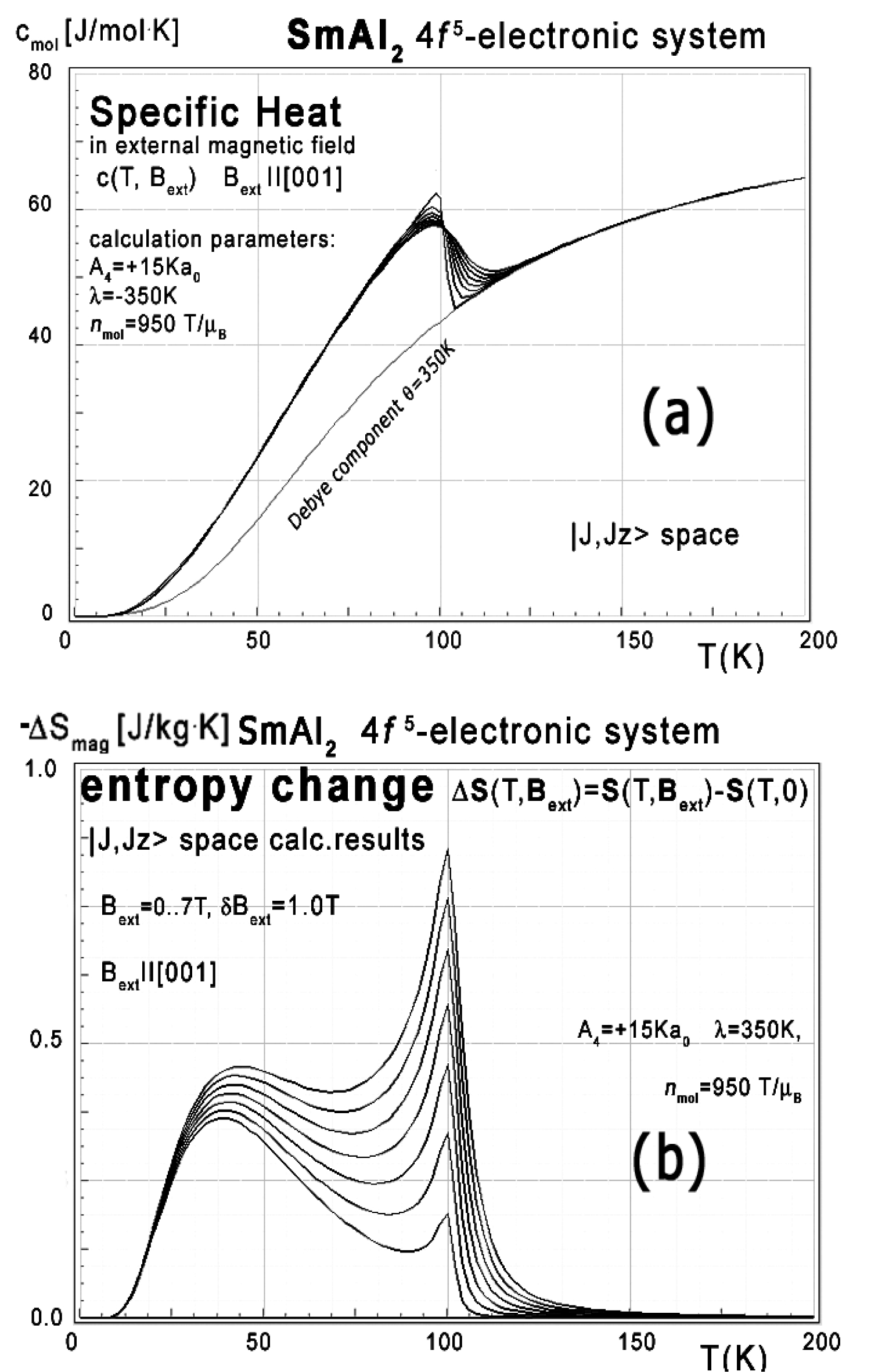
Figure 51: a) Calculated 4f-electron component of...
a) Calculated 4f-electron component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature for Sm3+ ions in SmAl2 under the influence of an external magnetic field applied along [001] direction; b) Calculated isothermal entropy change of 4f-electronic system vs. temperature (16) of Sm3+ ions in SmAl2 under the influence of an external magnetic field from 0 to 7 T applied along [001] direction.
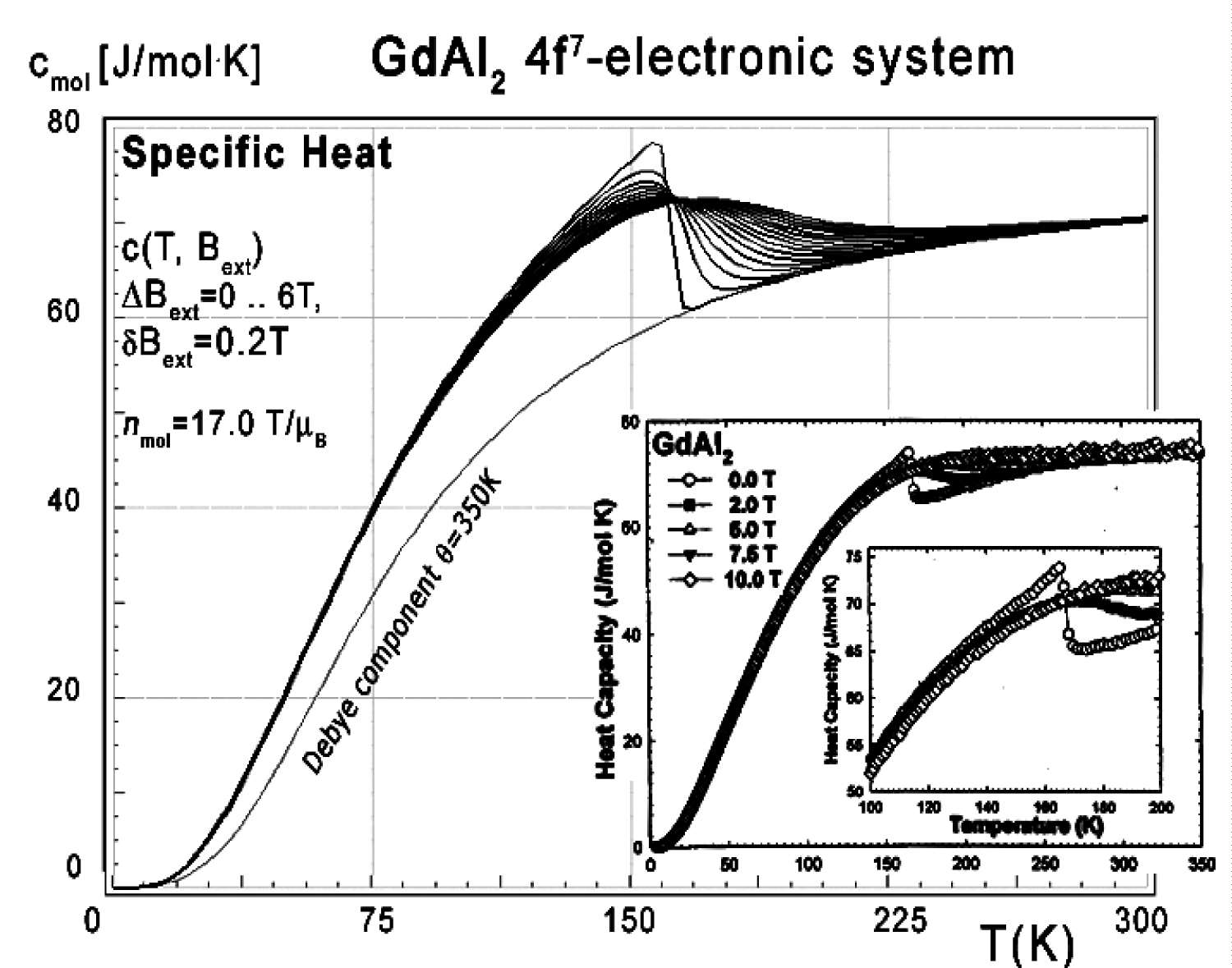
Figure 52: Calculated 4f-electron component...
Calculated 4f-electron component of molar specific heat (14) with Debye crystal lattice component (θ = 350 K) vs. temperature of Gd ions in GdAl2 under the influence of external magnetic field from 0 to 6 T with step 0.2 T. Inset: Experimental data from [31].

Figure 53: Calculated isothermal entropy change...
Calculated isothermal entropy change of 4f-electronic system vs. temperature (16) of Gd ions in GdAl2 under the influence of various values of external magnetic fields from 0 to 7.5 T with step 0.5 T. Inset: Isothermal entropy change obtained from experimental data, taken from [31]. Experimental data shown in inset corresponds with calculated solid curves for ΔBext = 2 T and ΔBext = 5 T.
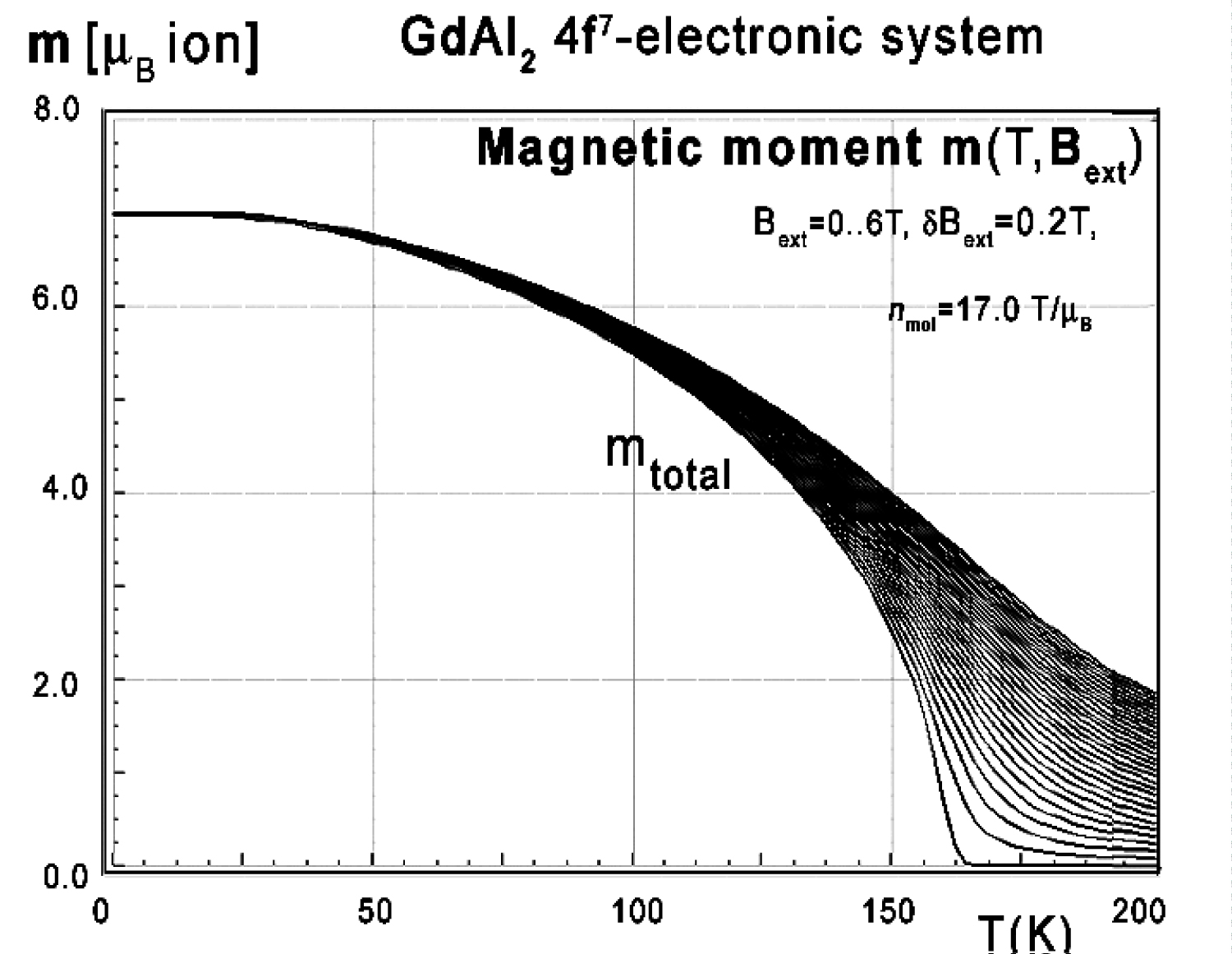
Figure 54: Calculated unidirectional total magnetic...
Calculated unidirectional total magnetic moment vs. temperature, calculated for Gd ions in GdAl2 under the influence of molecular magnetic field and various values of external magnetic field from 0 to 6.0 T with step 0.2 T.
References
- Michalski R, Zygadło J (2016) Describing the Fine Electronic Structure and Predicting Properties of Materials with ATOMIC MATTERS Computation System. International Journal of Physical and Mathematical Sciences 10: 294-300.
- Michalski R, Zygadło J (2016) Thermal dependences of single ionic, magnetic properties of materials in ordered state, calculated with ATOMIC MATTERS MFA computation system. Proceedings: 7th IIF-IIR International Conference on Magnetic Refrigeration at Room Temperature, Thermag VII - Torino, ITALY.
- Lima AL, Tsokol AO, Gschneidner KA Jr, Pecharsky VK, Lograsso TA, et al. (2005) Magnetic properties of single-crystal DyAl2. Phys Rev B 72: 024403.
- Purwins HG, Leson A (1990) Magnetic properties of (rare earth) Al2 intermetallic compounds. Adv Phys 39: 309-403.
- Pecharsky VK, Gschneidner KA, Pecharsky AO, Tishin AM (2001) Thermodynamics of the magnetocaloric effect. Phys Rev B 64: 144406.
- Von Ranke PJ, De Oliveira NA, Plaza EJR, De Sousa VSR, Alho BP, et al. (2008) The giant anisotropic magnetocaloric effect in DyAl2. Journal of Applied Physics 104: 093906.
- Gil LA, Campoy JCP, Plaza EJR, De Souza MV (2016) Conventional and anisotropic magnetic entropy change in HoAl2 ferromagnetic compound. Journal of Magnetism and Magnetic Materials 409: 45-49.
- Patra MS, Majumdar S, Giri S, Xiao Y, Chatterji T (2011) Magnetic and magnetoresistive properties of cubic Laves phase HoAl2 single crystal.
- Wang FW, Zhang XX, Hu FX (2000) Large magnetic entropy change in TbAl2 and (Tb0.4Gd0.6)Al2. Appl Phys Lett 77: 1360.
- Ribeiro PO, Alho BP, Alvarenga TST, Nóbrega EP, DeSousa VSR, et al. (2015) Theoretical investigations on magnetocaloric effect in Er1-yTbyAl2 series. Journal of Magnetism and Magnetic Materials 379: 112-116.
- Wikus P, Canavan E, Heine ST, Matsumoto K, Numazawa T (2014) Magnetocaloric materials and the optimization of cooling power density. Cryogenics 62: 150-162.
- Blaut A, Michalski R, Kocor M, Ropka Z, Baran AJ, et al. (2003) Electronic structure and magnetism of intermetallic NdAl2. Acta Physica Polonica B 34: 1261-1264.
- www.atomicmatters.eu.
- Elliot J, Stevens KWH (1953) The theory of the magnetic properties of rare earth salts: Cerium ethyl sulphate. Proc Roy Soc A 215: 437-453.
- Elliot J, Stevens KWH (1953) The theory of magnetic resonance experiments on salts of the rare earths. Proc Roy Soc A 218: 553-566.
- Rudowicz C, Chung CY (2004) The generalization of the extended Stevens operators to higher ranks and spins, and a systematic review of the tables of the tensor operators and their matrix elements. J Phys: Condens Matter 16: 5825-5847.
- Hutchings MT (1964) Point-charge calculations of energy levels of magnetic ions in crystalline electric fields. Solid State Phys 16: 227-273.
- Franse JJM, Radwański RJ (1993) Magnetic properties of binary rare-earth 3d-transition metal intermetallic compounds. In: Bushow KHJ, Handbook of Magnetic Materials. 7: 307-501.
- Radwański RJ, Michalski R, Ropka Z, Blaut A (2002) Crystal-field interactions and magnetism in rare-earth transition-metal intermetallic compounds. Physica B: Condensed Matter 319: 78-89.
- Szpunar B, Lindgard PA (1979) On the origin of the large magnetic anisotropy of rare earth-cobalt compounds. J Phys F: Metal Phys 9.
- de Gennes PG (1962) Indirect interactions between 4f shells in rare earth metals. J Phys Radium 23: 510.
- Wybourne BG (1970) Symmetry principles and atomic spectroscopy. J Wiley and Sons, New York.
- Abragam A, Bleaney B (1970) EPR of transition ions. Clarendon Press, Oxford.
- Michalski R, Zygadło J (2018) Predictions of thermomagnetic properties of Laves phase compounds: TbAl2, GdAl2 and SmAl2 performed with atomic matters mfa Computation System. Journal of Magnetism and Magnetic Materials 452: 415-426.
- White JA, Van Vleck JH (1961) Sign of knight shift in samarium intermetallic compounds. Phys Rev Lett 6: 412-413.
- Itou M, Koizumi A, Sakurai Y (2013) Spin and orbital magnetization loops obtained using magnetic compton scattering. Appl Phys Lett 102: 082403.
- Qiao S, Kimura A, Adachi H, Iori K, Miyamoto K, et al. (2004) Direct evidence of ferromagnetism without net magnetization observed by x-ray magnetic circular dichroism. Phys Rev B 70: 134418.
- Adachi H, Ino H, Miwa H (1999) Separation of the 4f-spin, 4f-orbital and conduction-electron magnetization from exotic thermomagnetic behavior for ferromagnetic Sm intermetallics. Phys Rev B 59: 11445.
- Adachi H, Ino H (1999) A ferromagnet having no net magnetic moment. Nature 401: 148-150.
- Kulkarni PD, Dhar SK, Provino A, Manfrinetti P, Grover AK (2010) Self-magnetic compensation and shifted hysteresis loops in ferromagnetic samarium systems. Phys Rev B 82: 144411.
- Dankov SY, Ivtchenko VV, Tishin A, Pecharsky VK (2000) Magnetocaloric Effect in GdAl2 and Nd2Fe17, conference paper. Advances in Cryogenic Engineering (Materials) 46: 397-404.
- Ribeiro PO, Alho BP, Alvarenga TST, Nóbrega EP, deSousa VSR, et al. (2013) Theoretical investigations on the magnetocaloric and barocaloric effects in TbyGd(1-y)Al2 series. Journal of Alloys and Compounds 563: 242-248.
Author Details
R Michalski1* and J Zygadło1,2
1Atomic Systems, Cracow, Poland
2Faculty of Mathematics and Computer Science, Jagiellonian University, Cracow, Poland
Corresponding author
R Michalski, Atomic Systems, M. Pszona 41/29, 31-462 Cracow, Poland.
Accepted: February 27, 2019 | Published Online: March 01, 2019
Citation: Michalski R, Zygadło J (2019) Simulated Thermomagnetic Properties of DyAl2, HoAl2 and ErAl2 Compounds in Comparison with the Results for TbAl2, GdAl2 and SmAl2 Calculated by ATOMIC MATTERS MFA Computation System. Int J Magnetics Electromagnetism 5:018.
Copyright: © 2019 Michalski R, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We present the results of calculations of magnetic properties of 3 compounds from Laves phase C15 family: DyAl2, HoAl2 and ErAl2 performed with a new computation system called ATOMIC MATTERS MFA. We compare these results with the recently published results for TbAl2, GdAl2 and SmAl2. The calculation methodology was based on the localized electron approach applied to describe the thermal evolution electronic structure of rare-earth R3+ ions over a wide temperature range and to compute magnetocaloric effect (MCE). Thermomagnetic properties were calculated based on the fine electronic structure of 4f9, 4f10 and 4f11 configurations of the Dy3+, Ho3+, Er3+ ions, respectively. Our calculations yield the magnetic moment value and direction; single-crystalline magnetization curves in zero field and external magnetic field applied in various directions of m(T,Bext); the 4f-electronic components of specific heat c4f(T,Bext); and temperature dependence of the magnetic entropy and isothermal entropy change with external magnetic field -ΔS(T,Bext). The cubic CEF parameter values used for DyAl2 calculations are taken from earlier research of A.L. Lima, A.O. Tsokol and recalculated for universal cubic parameters (Amn) for the RAl2 series. Our studies reveal the importance of multipolar charge interactions when describing thermomagnetic properties of real 4f electronic systems and the effectiveness of an applied self-consistent molecular field in calculations for magnetic phase transition simulation.
Keywords
DyAl2, HoAl2, ErAl2, TbAl2, DyAl2, GdAl2, CEF, MFA, MCE, Atomic matters
Introduction
Condensed matter science research in advanced magnetic refrigerant materials has focused on the giant magnetocaloric effect since its discovery. This has advanced the development of near room-temperature magnetic cooling technology. Understanding and controlling the microscopic quantum mechanisms responsible for storing and releasing material entropy through controlled external magnetic field change processes is one of the biggest challenges in materials science.
The RAl2 (R = rare earth element) compounds are well known intermetallic materials with interesting magnetic properties at low temperatures. The magnetic properties of this series were studied intensively in the 1970s, but a new wave of interest in this compound family has appeared due to research into materials with a large Magnetocaloric Effect (MCE) for future magnetic refrigerators. We present the results of simulations performed by our ATOMIC MATTERS computation system [1,2] of thermomagnetic properties of DyAl2, HoAl2 and ErAl2. A few calculation results for the RAl2 compounds are compared with experimental data taken from the literature [3-11]. All the lanthanides combine with aluminum to form a RAl2 compound with the same crystalline structure. This structure is the so-called cubic Laves phase C15 and the point symmetry for the rare earth ion is 4-3 m.
The structure was named after the Swiss crystallographer who performed work on the prototype compound MgCu2. The CEF parameters describing the multipolar charge interaction of R ions in the crystal surrounding in this structure were agreed for both compounds and established by previous studies [3,4,12] for A4 = +7.164 Ka0 and A6 = -1.038 Ka0.
Computation System
All RAl2 calculations were performed with ATOMIC MATTERS MFA computation system [2], an extension of the ATOMIC MATTERS application [1] that describes the fine electronic structure and predicts basic magnetic and spectral properties of materials in a paramagnetic state. ATOMIC MATTERS MFA calculates magnetic, calorimetric and spectroscopic properties of atomic-like localized electron systems under the influence of Crystal Electric Field (CEF), spin-orbit coupling, and magnetic interactions, taken both as Mean Field Approximation (MFA) self-consistent, dynamic calculations and the influence of established external magnetic fields Bext [2]. ATOMIC MATTERS MFA calculates macroscopic properties of materials in defined temperature regions, especially around phase transition temperature, such as: Magnetic moment m(T,Bext) (spin and orbital, directional components); localized electron specific heat c4f(T,Bext); localized electron entropy with a useful tool-set for MCE; isothermal entropy change -ΔS(T,Bext) calculations; evolution of energy level positions; total free energy.
Both calculation systems contain advanced Graphic User Interface (GUI) with a system of hierarchical tabs for calculation results management, 3D interactive visualizations of potentials and fields based on OpenGL graphic engine, tools and databases for convenient and effective work. More up-to-date information about Atomic Matters computation systems is available on our web page [13].
Theoretical Background
The theoretical approach applied at the heart of ATOMIC MATTERS MFA computation system is deeply rooted in atomic physics. Taking into consideration the individual population of states of the fine electronic structure of ions/atoms at different temperatures according to Boltzmann statistics make it possible to define the temperature dependencies of single ionic properties. ATOMIC MATTERS MFA can simulate phase transitions of ionic/atomic systems according to dynamic calculations of the molecular field Bmol, simply defined as:
This interacts with ions to induce their magnetic moments. Such self-consistent calculations can only be performed after establishing the molecular field factor nmol that is closely related to the temperature of phase transitions TC.
For rapid calculations in a thermodynamically stable temperature region, ATOMIC MATTERS offers the following CEF + Spin-Orbit + Zeeman Hamiltonian according to the chosen calculation space of ground multiplet |J,Jz> or ground atomic term |L,S,Lz,Sz>, respectively [1]:
or
For all Hamiltonians: Bmn denotes CEF parameters, Omn are Stevens operators [14,15], λ is the spin-orbit constant, and gL and ge ≈ 2.002319 are the gyromagnetic factors of a whole ion or single electron, respectively. µB is the Bohr magneton and Bext is the external magnetic field. In all cases, calculations in the |L,S,Lz,Sz> space are more physically appropriate due to their completeness, but traditional calculations with base |J,Jz> can also be performed by our computation systems for comparisons and rapid estimations [2]. For calculating properties in temperatures around the magnetic phase transition point, a self-consistent methodology for molecular field calculation called Mean Field Approximations (MFA) is applied. The idea behind this method is the estimation of direction and value of the magnetic field (molecular field) generated by ions at a defined temperature, and calculation of the influence of this magnetic field for electronic state structures of ions. In a selected calculation space, according to (1) we define a molecular field as an expected value of the total moment of the 4f electronic subshell multiplied by the molecular field, inter ionic exchange factor nmol:
Or
Where gL and ge ≈ 2.002319 are gyromagnetic factors. On the basis of the calculated electronic level structure Ei(T), the directional components of magnetic moments are established for all identical ions. This means that Hamiltonian matrix diagonalization is performed for all defined temperature steps recurrently, in contrast to simple ATOMIC MATTERS calculations [1], which diagonalize matrices one time for a single run and deduce all thermodynamic properties from the stable discrete energy level structure obtained. This self-consistent procedure provides temperature-dependent energy level structure and has one only free parameter, nmol, called the molecular field parameter. The value of nmol is closely related to the phase transition temperature TC of the macroscopic structure of ions. The formal expression of the full Hamiltonian used by ATOMIC MATTERS MFA computation system, according to the chosen calculation space |J,Jz> or |L,S,Lz,Sz>, respectively, has the form:
Or
The eigenvectors of the Hamiltonian are described according to the selected calculation base by the total momentum quantum numbers |J,Jz> or spin and orbit quantum numbers |L,S,Lz,Sz>. Using the commutation relations of the angular momentum operators, we obtain information about expected values of the projections of the magnetic momentum of all electronic states at chosen temperature [2]:
Where: α indexes directional components, i - numbers the Hamiltonian eigenstates, while Γi represents the expected value of the total angular momentum along the α-axis in the i-th state:
All calculations can be done for 3D (x,y,z) real space by using complex Hamiltonian matrix elements defined by full expressions of extended Stevens Omn operators [16]. Mostly for comparison with traditional calculation results, ATOMIC MATTERS also offers a 2D (x,z) calculation methodology of a simplified model of CEF interactions defined by Stevens Omn operators with real number matrix elements only [14,15,17].
Taking into consideration the possibility of the thermal population of states, we automatically obtain the thermal evolution of single ion properties of the whole compound [18,19].
Under the thermodynamic principle at temperature T = 0 K only the ground state is occupied. In this situation, the magnetic moment of the ion is exactly equal to the momentum of the ground state. If the temperature rises, the probability of occupying higher states increases according to Boltzmann statistics. The number of ions with energy Ei within a system at temperature T is:
Where N0 ≈ 6.022·1023 mol-1 (Avogadro constant) and Z(T) is the sum of states. Knowing the sum of the states, we can determine the Helmholtz free energy F(T):
According to thermodynamic principles, the contribution of localized electrons to the total specific heat of materials can be calculated by numerical derivation of Helmholtz free energy:
This makes it possible to calculate entropy according to the well-known definition:
The value of electronic entropy for a defined temperature is difficult to compare, but the isothermal change of the entropy of the system at given temperature is a very important material parameter that describes its thermomagnetic properties. Isothermal entropy change -ΔS(T,Bext), captured for different temperatures under the influence of different magnetic fields, is one the most important properties of a material that describes its usefulness as a magnetocaloric material. The value -ΔS(T,Bext), which was extracted from experimental specific heat measurements, is often presented as a basic description of the magnetocaloric effect (MCE) of materials [3-7,9-11]. In our approach, isothermal entropy change can be directly calculated from (15) according to the definition:
ATOMIC MATTERS MFA also provides single-ionic magnetocrystalline anisotropy calculations that include full calculations (without Brillouin function approximation) of Ki(T) magnetocrystalline constants for defined temperature ranges according to the relations [20]:
Where: denotes thermal expected values of Stevens operators we defined according to C. Rudowicz [11]. The exchange interactions simulated according to MFA methodology defined by (1) provide simulated properties strongly dependent on only one parameter, nmol, which is closely related to the temperature of phase transitions TC. It is easy to find the value of nmol for correct TC, but the value of this parameter can be estimated according to de Gennes scaling [21]:
De Gennes scaling is also a useful tool for nmol estimation, as charge surroundings can be transferred between ions in series. The CEF part of Hamiltonian contains Stevens CEF parameters Bmn. The values of these parameters are only appropriate for a defined ion. The recalculation of Bmn parameters defined for an ion A in the crystal lattice surrounding of ion B in the same crystalline position follows the simple scheme:
Stevens Bmn parameters can be expressed by universal Amn parameters, according to the calculation space used, as follows:
Where values of 2, 4, 6-th power of the average radius of 4f shell
Calculation Results for DyAl2
The CEF parameters used for DyAl2 were originally estimated by H.G. Purwins and A. Leson [4] and confirmed by A.L. Lima, et al. [3].
The local symmetry of coordinating charges of R3+ ions defines number of non-zero CEF parameters. In case of cubic crystal field, there are only two non-zero CEF parameters describing the coordinating potential. The relation between cubic CEF parameters B4 and B6 and generally defined CEF parameters used in Hamiltonians (2), (3), (6) and (7) is simple:
The parameters were provided in cubic Stevens notation: B4 = -(5.5 ± 1.2).10-5 meV and B6 = -(5.6 ± 0.8).10-7 meV. We recalculated the values of Stevens parameters to obtain universal, ion-independent CEF notation Amn according to (19) and (20). The parameters A4 = +7.164 Ka0 and A6 = -1.038 Ka0 obtained in this manner define charge surroundings of R ion in a crystal lattice of RAl2. The visualization of this potential is shown in Figure 1. The triangular shapes that are connected to the location of the coordinating Al ions are located symmetrically in cubic surroundings and reflect the atom position in the elementary cell of Laves phase shown in Figure 2.
The intermetallic compound DyAl2 has strong magnetocaloric properties at low temperatures. This compound has been extensively studied both theoretically and experimentally [3-6].
In this section, we present the results of an investigation of the magnetic and magnetocaloric properties of a DyAl2 single crystal. We have attributed the magnetism of DyAl2 to the Dy3+ ions and calculated the fine electronic structure of the 4f9 electronic system in cubic symmetry taking into account the crystal field and inter-site, spin-dependent exchange interactions. The energy level scheme derived is associated with the reduction of the degeneracy of the lowest atomic term 6H given by Hund's first two rules.
The full calculated energy level structure in the |L,S,Lz,Sz> calculation space is shown in Figure 3. The obtained overall splitting is strongly dependent on the strength of spin-orbit intra-atomic interactions. We use the free-ion value of the spin-orbit constant of Ho3+ ions λ = -550 K [22,23] and obtain an overall splitting of 6H atomic term of about 15000 K = 1.3 eV. Details of ground states structure are shown in Figure 4.
In the absence of an external magnetic field, the induced molecular field splits and moves into degenerated states. The value of the molecular field factor established for DyAl2, which reproduces TC well at about 63 K, is nmol = 3.6 T/μB. Above TC, the material is in a paramagnetic state and the ground state of Dy ions is degenerated. The ground quartet consists of two quasi-doublets. The wave functions of the ground paramagnetic state of Dy ions in DyAl2 can be expressed in |Jz> notation:
The molecular field splits these states at T < TC. The value of the molecular field changes and at T = 0 (absolute zero) Bmol = 23.6 T and its direction is along the [100] crystal direction, which is the x-axis in our CEF potential picture from Figure 2. In this condition, the wave function of the ground singlet gets the form:
The influence of the external magnetic field applied along different crystal directions for the structure of the lowest electronic states is shown in Figure 5 and Figure 6. The comparison between the effects of the external magnetic field applied along different directions reveals the appearance of an anomaly in the level structure if an external field is applied along the [110] crystal direction. This anomaly corresponds to the specific heat curve from Figure 7, computed in the same external field direction. The specific heat of DyAl2 (spec. heat of 4f9 electronic system + Debye crystal lattice component) shown in Figure 7 was calculated for the same external field conditions as experimental measurements from [3]. Excellent agreement between calculated specific heat and experimental data is also confirmed if the external magnetic field is applied along the [100] direction. The results of this calculation and reference measurements from [3] are shown in Figure 8.
Calculations of electronic structure under the influence of an external magnetic field applied along the [111] direction were also performed. Energy level structure calculated for external magnetic field in this direction does not contain anomalies and is similar to calculations performed for Bext along the easy magnetization [100] direction, as shown in Figure 5. Specific heat calculated in these conditions is shown in Figure 8. It can be seen in Figure 7, Figure 8 and Figure 9 that the 'peak' on specific heat curve is softened with increased value of external magnetic field. This is expected and can be attributed to more smooth changes in the energy levels structure (compare Figure 4 for B = 0 T and Figure 5 for B = 1 T) that results in less rapid changes in total energy.
Collected data of specific heat makes it possible to calculate isothermal entropy change -ΔS(T,Bext) according to (16), the same methodology as used by experimentalists [3-7]. Isothermal entropy change calculated with various external magnetic fields applied along all main directions of cubic structure is presented in Figure 10, Figure 11 and Figure 12. The reference data taken from experimental measurement [3] is shown in the insets.
The anisotropic behavior of calculated thermomagnetic properties is reflected in the magnetocrystalline anisotropy constant calculations. The results of Ki(T) calculations according to (17) in the absence of external magnetic field are shown in Figure 13.
For completeness, magnetic moment calculations vs. temperature under various external magnetic field conditions were performed. The results of m(T,Bext) are presented in Figure 14, Figure 15 and Figure 16. Figure 14 clearly confirms the [100] direction as an easy magnetization axis. The applied external magnetic field along this direction confirms perfect parallel directions of magnetic vector and external magnetic field (note: in cubic symmetry [100] = [010] = [001]).
Magnetic moment calculated in an external magnetic field parallel to the [110] direction reveals unusual behavior of the directional component of the total moment. Similar behavior of magnetic moment directions was reported in [3-5].
Calculation Results for HoAl2 and ErAl2
Here we present the results of an investigation of the magnetic and magnetocaloric properties of a HoAl2 and ErAl2 single crystal. The predictions of properties are completely achieved without any free parameters. We use established cubic CEF for DyAl2 parameters in Stevens notation from [4] and recalculated them for Ho3+ and Er3+ ions.
As above, we attributed the magnetism of HoAl2 and ErAl2 and the magnetism of HoAl2 to the Ho ions and performed calculations of the fine electronic structure of the 4f10 and 4f11 electronic systems, respectively. All calculations was performed for cubic symmetry, taking into account the crystal field and inter-site, spin-dependent exchange interactions. The energy level scheme derived is associated with the reduction of the degeneracy of the lowest atomic term (5I and 4I for Ho and Er ions, respectively) given by Hund's first two rules. The value of molecular field factor nmol for HoAl2 and ErAl2 was established according to nmolDy = 3.6 T/μB for DyAl2 and de Gennes scaling (18). The comparison between experimentally found Curie temperature TC and de Gennes scaling is shown in Figure 17.
Experimental values of TC for RAl2 compounds [3-7] and the theory are in good agreement for heavy Rare Earths elements from Gd(4f7) to Yb(4f13). De Gennes relations (11) make it possible to establish molecular field factor for HoAl2 nmolHo = 2.1 T/μB and for ErAl2 nmolEr = 0.95 T/μB.
Calculated properties of HoAl2 single crystals
The electronic configuration of 67Ho atoms consists of a closed shell inactive atomic core [54Xe], electronic system 4f10 and outer electrons 5d16s2. We attributed the magnetic properties of HoAl2 compound as an effect of properties of 4f10 electronic system under the influence of electromagnetic interactions defined according to the description in the theory section. The starting point of our analysis is the ground atomic term 5I with quantum number of orbital angular momentum L = 6 and total spin S = 2.
The full calculated energy level structure in |L,S,Lz,Sz> calculation space is shown in Figure 18. The obtained overall splitting is strongly dependent on the strength of spin-orbit intra-atomic interactions. We used free-ion value of the spin-orbit constant of Ho3+ ions λ = -780 K [22] and obtained overall splitting of 2F atomic term at about 20350 K = 1.753 eV.
Details of ground states structure are shown in Figure 18.
In the absence of an external magnetic field, the induced molecular field splits and moves into degenerated states. The value of the molecular field factor established for HoAl2 which reproduces TC well at about 36 K is nmol = 2.1 T/μB Figure 19.
Above TC, in a paramagnetic state, the ground state is degenerated and consists of 3 states. The ground triplet wave functions of ground state of Ho ions (4f10 electronic system) in HoAl2 in a paramagnetic state can be expressed in |Jz> notation as:
A molecular field splits these states at T < TC. The value of the molecular field changes, and at T = 0 (absolute zero) Bmol = 13 T and its direction is along the [110] crystal direction. In this condition, the wave function of a ground singlet gets the form:
The electronic structure obtained in the absence of an external magnetic field is fragile; even a small magnetic field applied along the [100] or [111] direction forces the structure to change the order of states and creates an anomaly at low temperatures. The influence of a small external magnetic field applied along the [111] direction for the structure of the lowest electronic states is shown in Figure 20. The position of this anomaly corresponds with peaks on specific heat curves. The calculated specific heat for a HoAl2 single crystal under the influence of an external magnetic field applied along various crystal directions is presented in Figure 21, Figure 22 and Figure 23.
A closer look at the unusual behaviour of the 4f-electron component of specific heat simulated under the influence of an external magnetic field along the diagonal [110] direction is shown in Figure 23.
As in the case of DyAl2, collected specific heat data allows us to calculate isothermal entropy change -ΔS(T,Bext) according to (16), the same methodology as used by experimentalist [3-7]. Isothermal entropy changes calculated with various external magnetic fields applied along all main directions of a cubic structure are presented in Figure 24, Figure 25 and Figure 26. Note that our calculations give negative values of -ΔS at low temperatures (below 20 K) with magnetic field applied along the [100] direction - however, this surprising result is in good agreement with experimental data [8]. This suggests that HoAl2 can exhibit 'inverse' magnetocaloric effect at very low temperatures.
The anisotropic behavior of calculated thermomagnetic properties is reflected in magnetocrystalline anisotropy constant calculations. The results of Ki(T) calculations according to (17) in the absence of an external magnetic field are shown in Figure 27.
The results of Ki(T) calculations according to (17) under the influence of external magnetic field Bext = 1 T applied along the [100] direction are shown in Figure 28.
For completeness, magnetic moment calculations vs. temperature under various external magnetic field conditions were also performed. The results of m(T,Bext) are presented in Figure 29, Figure 30 and Figure 31. The simulated thermal evolution of magnetic moment components under the influence of external magnetic field along the [110] direction shown in Figure 30 clearly confirms the [110] direction as an easy magnetization axis of HoAl2 in lowest temperatures. The applied external magnetic field along this direction confirms perfect parallel directions of magnetic vector and induced external magnetic field.
Magnetic moment calculated in external magnetic field parallel to the [111] and [100] direction reveals unusual behavior of the directional component of total moment. Similar behavior of magnetic moment directions was reported in [10], but most of the calculated properties of HoAl2 presented in this paper still await experimental verification.
We found only a few reports about measurements of thermomagnetic properties of HoAl2 single crystals. Some experimental comparative data of isothermal entropy change measured on HoAl2 single crystals is provided by L.A. Gil, et al. [7], and interesting entropy change is provided by M. Patra, et al. [8]. All experimental data from [4,5] confirms the correctness of our approach in thermomagnetic properties calculations of HoAl2.
Calculation of properties of ErAl2 single crystals
The electronic configuration of Er atoms consists of a closed shell inactive atomic core [54Xe], electronic system 4f11 and 'outer electrons' 5d16s2. We attribute the magnetic properties of ErAl2 compound to be an effect of properties of 4f11 electronic system under the influence of electromagnetic interactions defined according to the description in the theory section. The starting point of our analysis is the ground atomic term 4I with quantum number of orbital angular momentum L = 6 and total spin S = 3/2.
The full calculated energy level structure in |L,S,Lz,Sz> calculation space reveals good separation of ground multiplet 4I15/2 states from the rest of eigenstates of the fine electronic structure. The overall energy levels splitting is strongly dependent on the strength of spin-orbit intra-atomic interactions. We used free-ion value of the spin-orbit constant of Er3+ ions λ = -1170 K [17] and obtained overall splitting of 4I atomic term at about 22900 K = 1.97 eV. Details of ground multiplet 4I15/2 states structure are shown in Figure 32.
In the absence of an external magnetic field, the induced molecular field at T < TC splits degenerated states. The value of the molecular field factor established according to de Gennes scaling [16] for ErAl2 which reproduces TC well at about 11 K is nmol = 0.95 T/μB. Above TC, in a paramagnetic state, the ground state is degenerated. The ground quartet consists of two quasi-doublets. The wave functions of ground state of Er (4f11 electronic system) ions in ErAl2 in a paramagnetic state can be expressed in |Jz> notation as:
A molecular field split these states at T < TC. The value of the molecular field changes, and at T = 0 (absolute zero) Bmol = 4.46 T and its direction is along the [110] crystal direction. In this condition the wave function of a ground singlet gets the form:
The structure of states is sensitive on external magnetic field influence. The effect of an external magnetic field Bext = 1 T applied along the [111] direction for the structure of the lowest electronic states is shown in Figure 33.
The energy level structure makes it possible to calculate the 4f-electron component of specific heat. The result of calculation of specific heat under the influence of an external magnetic field compared to experimental data from [11] is shown in Figure 34, Figure 35 and Figure 36. We present results for different external magnetic field directions since measurements of specific heat in [11] were obtained for a polycrystalline sample which can be seen as an 'average' of randomly directed single crystals.
Again, collected specific heat data makes it possible to calculate isothermal entropy change -ΔS(T,Bext) according to (16), the same methodology as used by experimentalist [3-8]. Isothermal entropy change calculated with various external magnetic fields is presented in Figure 37, Figure 38 and Figure 39.
The anisotropic behavior of calculated thermomagnetic properties reflects in magnetocrystalline anisotropy constant calculations. The results of Ki(T) calculations according to (17) in absence of external magnetic field are shown in Figure 40.
For completeness, magnetic moment calculations vs. temperature under various external magnetic field conditions was performed. The results of m(T,Bext) are presented in Figure 41, Figure 42 and Figure 43.
Magnetic moment calculated in external magnetic field parallel to [111] and [110] directions reveals unusual behavior of the directional component of total moment. The electronic system seems to be easy switchable between those crystallographic directions. The low-temperature easy magnetization axis along the [110] direction easily transforms into [111]. The external magnetic field under Bext < 0.01 T changes directional components distribution of total magnetic moment of Er ions (compare Figure 42 and Figure 43).
Similar behavior of magnetic moment directions was reported in [7], but most of the presented results of calculations of properties of ErAl2 still await experimental verification.
Calculated Properties of TbAl2, SmAl2 and GdAl2 Single Crystals
We performed electronic structure calculations for Tb3+, Sm3+ and Gd3+ in the RAl2 C-15 crystal structure. Details of obtained results were published in [24]. In this section we present selected results of thermomagnetic properties of these compounds.
Calculated thermomagnetic properties of TbAl2
The 65Tb atoms contain electronic structure that consists of a closed shell inactive atomic core [54Xe], electronic system 4f8 and outer electrons 5d16s2. We attributed the magnetic properties of TbAl2 compound as an effect of properties of 4f8 electronic system under the influence of electromagnetic interactions defined according to the description in the theory section. The starting point of our analysis is the ground atomic term 2F with the quantum number of orbital angular momentum L = 3 and total spin S = 3.
The full calculated energy level structure in |L,S,Lz,Sz> calculation space is shown in Figure 44. The obtained overall splitting is strongly dependent on the strength of spin-orbit intra-atomic interactions. We used free-ion value of spin-orbit constant of Tb3+ ions λ = -410 K [18] and obtained overall splitting of 2F atomic term at about 8620 K = 0.743 eV.
In the absence of an external magnetic field, the induced molecular field splits degenerated states. The value of the molecular field factor established for TbAl2 which reproduces TC well at about 105 K is nmol = 7.0 T/μB.
Above TC, in a paramagnetic state, the ground state is degenerated. The ground quartet consists of two quasi doublets. The wave functions of the ground state of Tb (4f8 electronic system) ions in TbAl2 in a paramagnetic state can be expressed in |Jz> notation as:
The molecular field splits these states at T < TC. The value of the molecular field changes, and at T = 0 (absolute zero) Bmol = 42 T and its direction is along the crystal [110] direction. In this condition the wave function of a ground singlet gets the form:
The electronic structure obtained in the absence of an external magnetic field is extremely fragile; even a small magnetic field applied along [100] or [111] direction forces the structure to change the order of states and creates an anomaly at low temperatures. The influence of a small external magnetic field applied along [111] direction for the structure of the lowest electronic states is shown in Figure 45b. The position of this anomaly corresponds with peaks on specific heat curves. The calculated specific heat for a TbAl2 single crystal under the influence of an external magnetic field applied along various crystal directions is presented in Figure 45.
The closer look at the unusual behaviour of the 4f-electron component of specific heat simulated under the influence of an external magnetic field along 'diagonal' [111] direction is shown in Figure 46a.
We have not found comparative experimental data for specific heat measurements, but F.W. Wang [9] provides data of measured specific heat change Δc(T,Bext) defined as:
For measurements for ΔBext = 5 T. Comparison between data from [9] and our simulations of Δc(T,Bext) is shown in Figure 46b. The simulation for ΔBext = 5 T in this figure is represented by a solid line.
Collected data of specific heat allows to calculate isothermal entropy change -ΔS(T,Bext) according to (16), the same methodology as used by experimentalists [3-7]. Isothermal entropy changes calculated with various external magnetic fields applied along all main directions of the cubic structure are presented in Figure 47. Note negative values of -ΔS at temperatures below 40 K for [100] and [111] directions - these results still await experimental confirmation.
For the sake of completeness, calculations of magnetic moment vs. temperature under various external magnetic field conditions were also performed. The graphs of m(T,Bext) are presented in Figure 10. The simulated thermal evolution of magnetic moment components under the influence of external magnetic field along [110] direction shown in Figure 48b clearly confirms [110] direction as an easy magnetization axis of TbAl2. The applied external magnetic field along this direction confirms perfect parallel directions of magnetic vector and external magnetic field (note: in cubic symmetry [110] = [011] = [101]).
Magnetic moment calculated in external magnetic field parallel to [111] and [100] direction reveals unusual behavior of the directional component of total moment. Similar behavior of magnetic moment directions was reported in [4], but most of the presented results of calculations of properties of TbAl2 still await experimental verification. We found only a few reports about measurements of thermomagnetic properties of TbAl2 single crystals. Some experimental comparative data of isothermal entropy change measured on TbAl2 single crystals is provided by P.O. Ribeiro, et al. [10], and interesting specific heat change measured on polycrystalline sample is provided by F.W. Wang, et al. [9]. All experimental data from [3-6] confirm the correctness of our approach in predicting the thermomagnetic properties of TbAl2.
Calculated thermomagnetic properties of SmAl2
In case of Sm3+ ions in SmAl2, the spin and orbital magnetic moments of the magnetic ions under condition of defined CEF are found always antiparallel coupled and the magnitude of its orbital magnetic moment is always larger than that of the spin one. Calculations of electronic states in a paramagnetic state (ATOMIC MATTERS methodology) reveals this antiparallel coupling between spin and orbital momentum. The full structure of energy level in a paramagnetic state, calculated in |L,S,Lz,Sz> space, together with expected values of angular momentum (spin and orbital) of particular states is shown in Figure 49.
The obtained electronic structure clearly demonstrates spin and orbital compensation of expected values of spin and orbital component of total angular momentum.
Calculations of energy level structure according to MFA methodology, in simplified |J,Jz> space, according to (6) (ground J-multiplet only) provide primitive energy level structure shown in Figure 49c. According to the described methodology we calculated the total moment m(T) under the influence of molecular field (Figure 50). To achieve Curie temperature TC of about 120 K, the value of the molecular field parameter was estimated at about nmol = 950 T/μB. We do not have an explanation for such a large value of nmol. The value of the ordered moment at T = 0 K achieved that way is approx. m(0) = 0.73 μB, about four times higher than the experimental value mexp = 0.2 μB [25-30].
The energy level structure makes it possible to calculate localized electron specific heat under the influence of an external magnetic field as shown in Figure 51a.
Calculated thermomagnetic properties of GdAl2
The electronic configuration of Gd atoms consists of a closed shell inactive atomic core [54Xe], a half filled 4f shell (e.g. electronic system 4f7), and outer electrons 5d16s2. We attribute the magnetic properties of GdAl2 compound to be an effect of properties of 4f7 electronic system under the influence of electromagnetic interactions defined according to the description in the theory section. The starting point of our analysis is the ground atomic term 8S with the quantum number of orbital angular momentum L = 0 and total spin S = 7/2. This means Gd is a pure spin system. According to this, CEF does not interact with electronic states of the ground atomic term 8S. In consequence, according to our approach, there is no source of single ionic anisotropy of Gd+3 ions with 4f7 electronic system. Inter-atomic magnetic interactions according to our MFA approach have pure isotropic nature (4) and (5), therefore the obtained properties of GdAl2 are absolutely identical despite the direction of the magnetic field applied. The value of molecular field factor nmol for GdAl2 was established according to de Gennes scaling [10] nmolGd = 17.0 T/μB. The calculated energy level structure is shown in Figure 11a.
In the absence of an external magnetic field, the ground term of the 4f7 electronic system is fully degenerated. A self-consistent molecular field splits these states at T < TC. The value of the molecular field changes, and at T = 0 (absolute zero) Bmol = 63 T.
The calculations of electronic structure under the influence of an external magnetic field applied along [111] direction was also performed. The energy level structure calculated for the external magnetic field in this direction does not contain any anomalies. Specific heat calculated in this condition is shown in Figure 52.
Collected specific heat data makes it possible to calculate isothermal entropy change -ΔS(T,3) according to (16), the same methodology as used by experimentalists [3-7]. Isothermal isotropic entropy change calculated with various values of external magnetic field is presented in Figure 53. The reference data taken from experimental measurement [3] is shown in the insets.
The isotropic behavior of calculated thermomagnetic properties agrees with experimental data [31,32]. For completeness, magnetic moment calculations vs. temperature under various external magnetic field conditions were performed - the results are presented in Figure 54.
Conclusions
In the first step we performed calculations of Dy3+ ions in the cubic CEF characteristic for Laves Phase C15 adequate for RAl2 crystals. Single-ionic thermomagnetic properties of DyAl2 calculated with the ATOMIC MATTERS MFA computation system bases of the local symmetry of the Dy in the point symmetry for R ion is 4-3 m. The local symmetry of R ions in this structure is cubic, which significantly simplifies the analysis. All the calculations were performed with only 2 cubic CEF parameters and molecular field factor nmol.
The excellent agreement between obtained calculated thermomagnetic properties and the reference data confirms the effectiveness of our theoretical approach. Although, the single atomic approach seems to be very effective methodology for description 4f electronic systems, the complete analysis of magnetic properties of macroscopic materials needs more extended models, e.g. simulations domain structure by many-ionic interactions.
Thermomagnetic properties of materials such as ΔS(T,Bext) and m(T,Bext) are currently an area of re-interest of researchers due to searching for effective materials for refrigerators working on the basis of magnetocaloric effect. As we have shown, magnetocaloric properties of materials can be well predicted based on the knowledge of the CEF crystalline field for paramagnetic ions (responsible for MCE) in the analyzed material. There is, however, not much information on the magnetocaloric properties of materials, even well-known and tested for other functional aspects. There is a huge knowledge base regarding crystalline fields of thousands of chemical compounds in solid state. Our application is able to convert parameters of CF, CEF, ZFS and LF models written in various conventions (Wybourne, Racach, Stevens) to the universal CEF convention in the Amn parameter language. Thanks to this, it is a tool that allows researchers to easily get knowledge about thermomagnetic properties of a material based on the methodology described in chapter 3, using the introduction of CEF coefficients to the software and allowing the researcher to select the convention. Recalculation of CEF coefficients between different compounds in the isostructural series leads to establishing a new set of crystal field parameters. With a significant confidence level we are able to predict properties of new materials, in particular their thermomagnetic behavior. The effectiveness of this methodology is confirmed by the presented calculation results for materials DyAl2, HoAl2, ErAl2, TbAl2, SmAl2 and GdAl2. According to established universal CEF parameters (Amn) for all RAl2 compounds, we performed similar calculations for HoAl2 and ErAl2 thermomagnetic properties. The local symmetry of the Ho and Er ions is cubic, which significantly simplifies the analyses. All the calculations were performed without free parameters. Very good agreement was obtained between thermomagnetic properties and experimental data confirms the effectiveness of our theoretical approach. Working with ATOMIC MATTERS MFA has revealed its high usefulness. The visual form of calculation results, full 3D interactive CEF potential visualization, intuitive tools for convention and unit recalculation, and the ability to compare data results all allow users to utilize the power of the application very effectively. In conclusion, we confirm that ATOMIC MATTERS MFA is a unique application that combines a package of tools for correctly describing the physical properties of atomic-like electron systems subjected to electromagnetic interactions in real materials. This is an accurate tool for calculating properties of ions under the influence of the electrostatic potential of definable symmetry and both external and inter-ionic magnetic fields taken as a mean field approximation in magnetically ordered state.