International Journal of Earth Science and Geophysics
(ISSN: 2631-5033)
Volume 4, Issue 2
Research Article
DOI: 10.35840/2631-5033/1820
Audio-Frequency Magnetotelluric Prospecting in the Mamfe Sedimentary Basin of Southwestern Cameroon
Jean Jacques Nguimbous-Kouoh1*, Theophile Ndougsa Mbarga2 and Eliezer Manguelle-Dicoum3
Table of Content
Figures
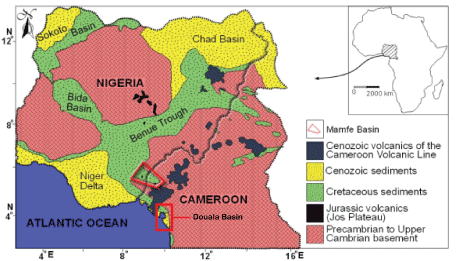
Figure 1A: Simplified geological map of Cameroon and Nigeria...
Simplified geological map of Cameroon and Nigeria showing the main sedimentary basins and location of the Mamfe Basin shown as an arm of benue trough in Cameroon (modified from Avbovbo, Ajonina, et al.) [24,42].
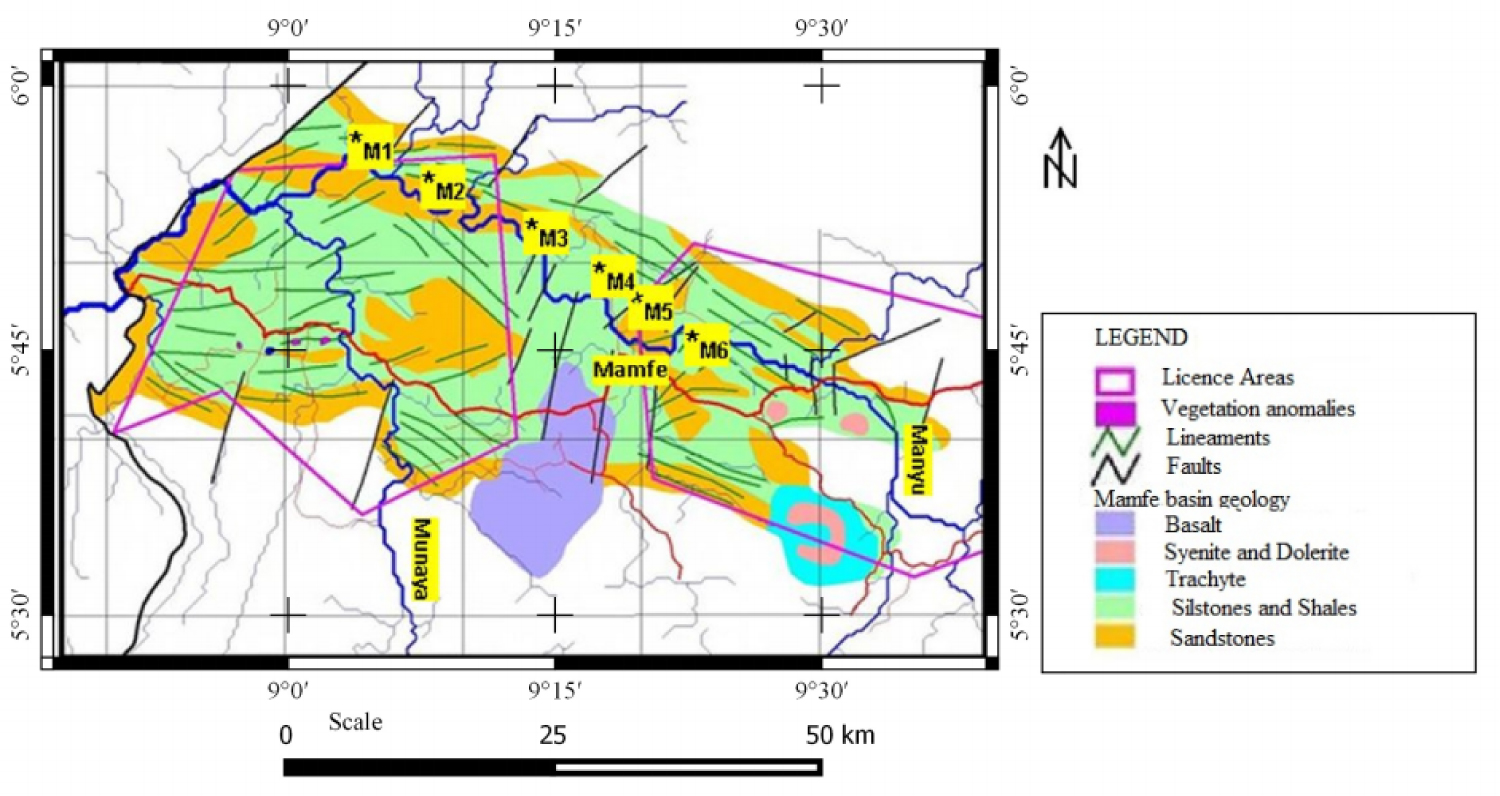
Figure 1B: Geologic map of Mamfe sedimentary basin...
Geologic map of Mamfe sedimentary basin (modified from Avbovbo, Ajonina, et al.) [24,42].
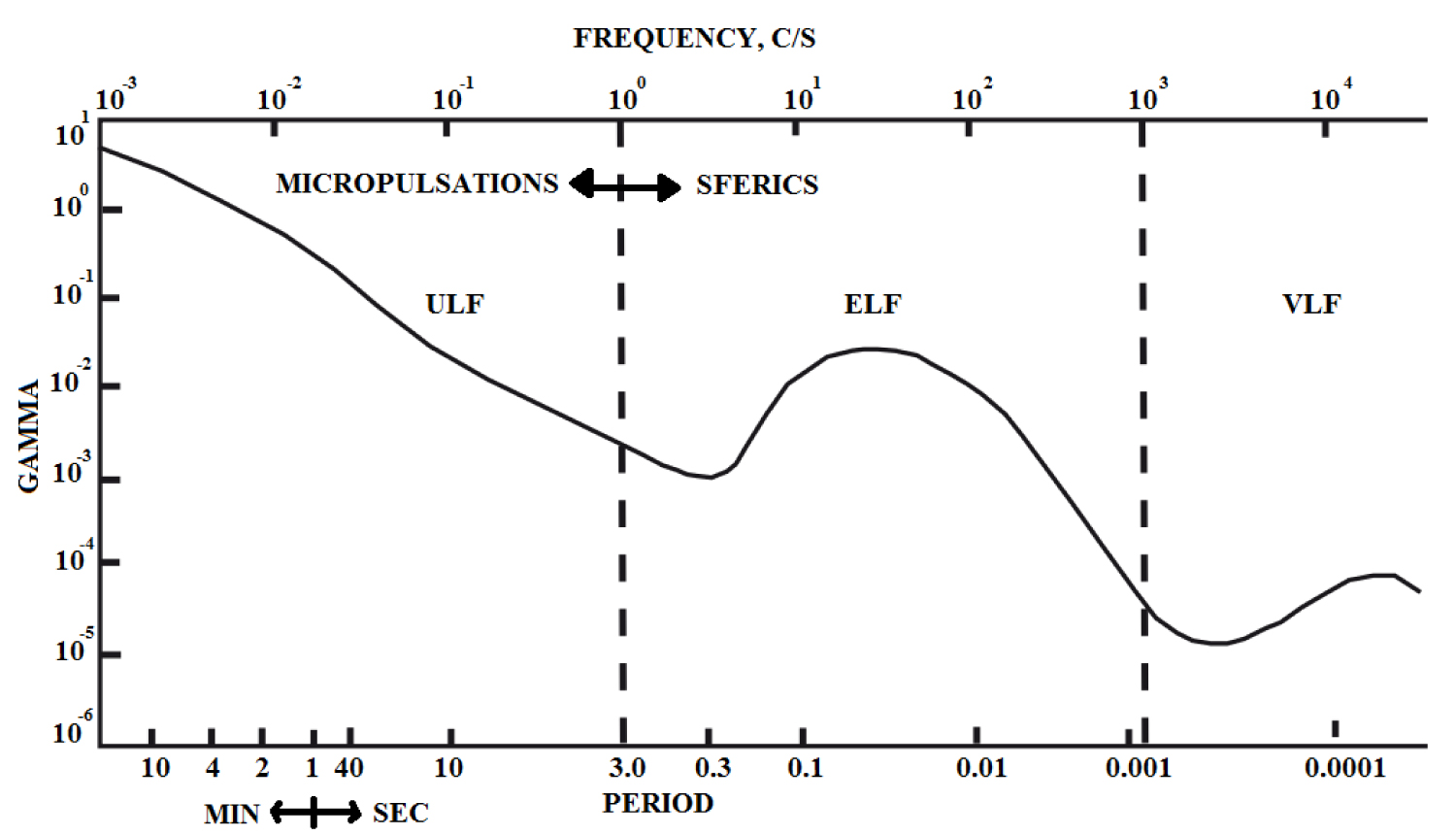
Figure 2: The natural magnetic field spectrum...
The natural magnetic field spectrum (modified from Bastani) [29].
Figure 3: Current sunspot cycle (modified from...
Current sunspot cycle (modified from Bastani) [29].

Figure 4: The setup of a magnetotelluric sounding...
The setup of a magnetotelluric sounding (modified from Bastani) [29].
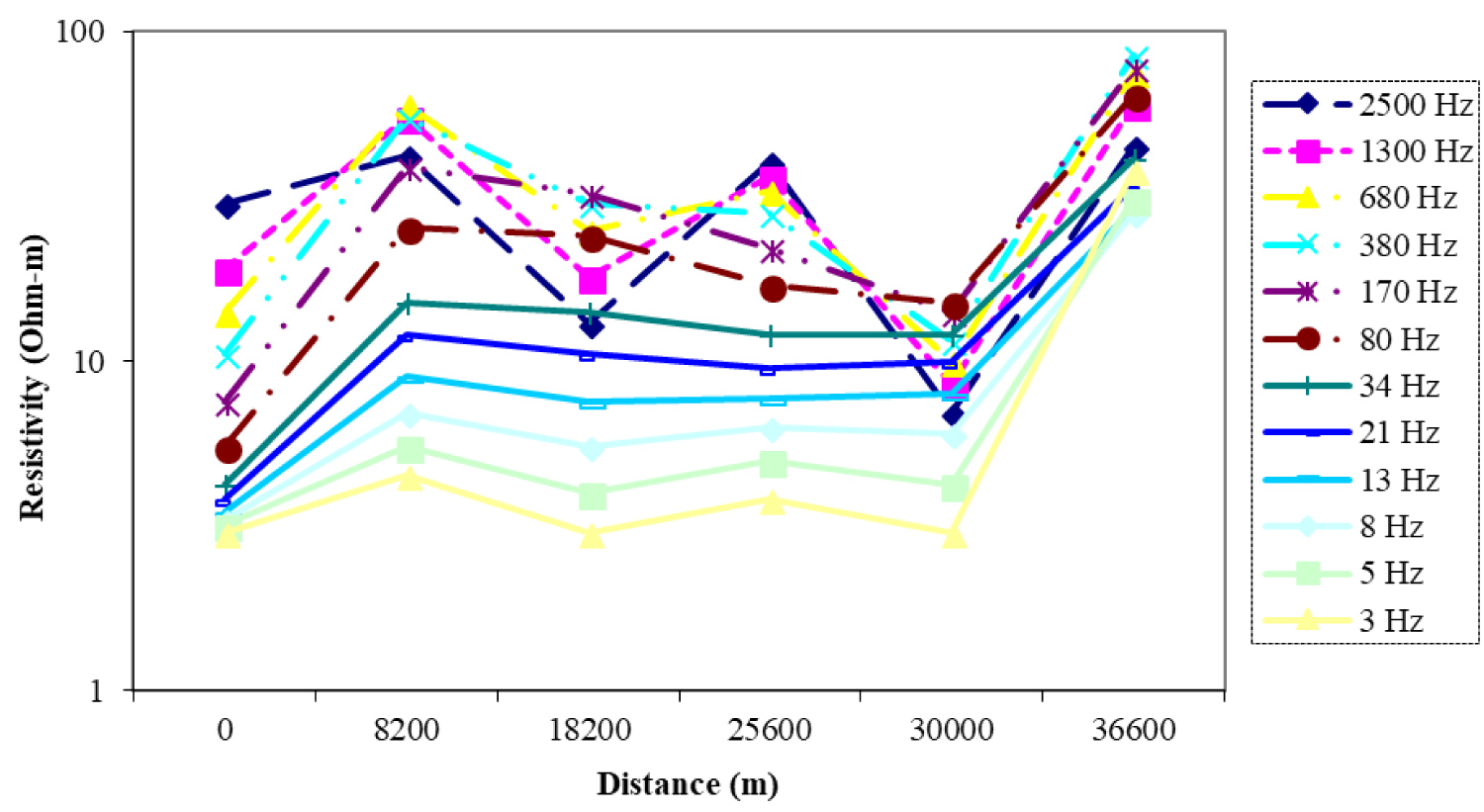
Figure 6A: Monofrequency electrical profiling TE mode E-W...
Monofrequency electrical profiling TE mode E-W.

Figure 6B: Monofrequency electrical profiling TM mode N-S...
Monofrequency electrical profiling TM mode N-S.
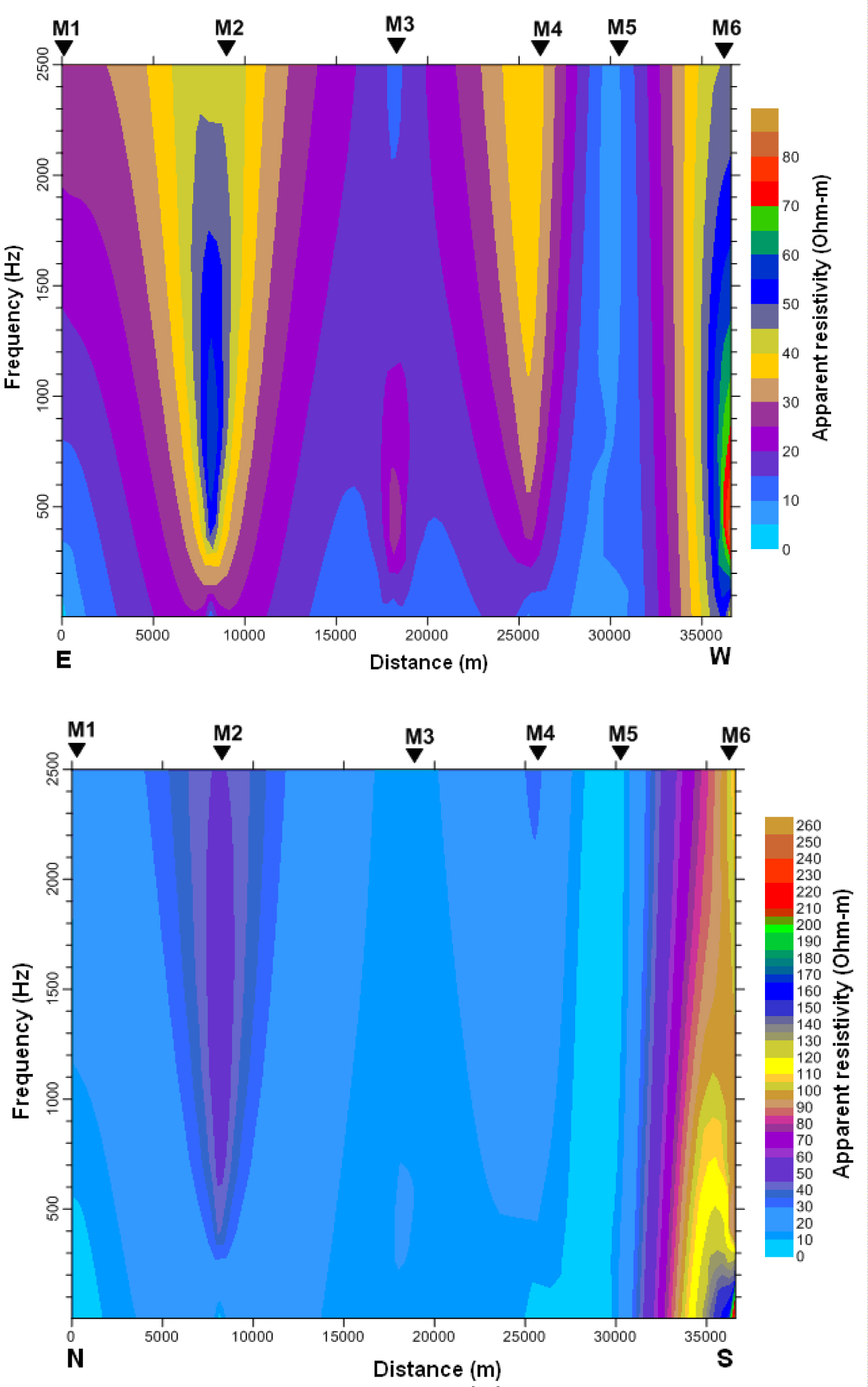
Figure 7: Pseudo-section of the TE and TM response across...
Pseudo-section of the TE and TM response across the profile. Contour intervals are the same for the TE and TM modes. a) Pseudo-section of the TE response across the profile; b) Pseudo-section of the TM response across the profile.

Figure 8: Geoelectric model of apparent resistivity...
Geoelectric model of apparent resistivity (different color scales are used to highlight underground structures).
References
- Alan D Chave, Alan G Jones (2012) The magnetotelluric method: Theory and practice. Cambridge University Press.
- Le Le Fur Y (1965) Basement-Cretaceous Mission. 1964-1965 report on the lead and zinc indices of the Gulf of Mamfe. BRGM Report, Cameroon, 30.
- Dumort JC (1968) Geological map of recognition at the scale 1/500000. Explanatory note on the Douala -West sheet. Federal Republic of Cameroon, Directorate of Mines and Geology of Cameroon, 69.
- Paterson, Grant, Watson (1976) Aeromagnetic studies on certain regions of the United Republic of Cameroon. Interpretation Report Canadian International Development Agency Toronto, 35.
- Fairhead JD, Okereke CS (1988) Depth to major density contrast beneath the West African rift system in Nigeria and Cameroon based on the spectral analysis of gravity data. Jour of African Earth Science 7: 769-777.
- Fairhead JD, Okereke, Nnange JM (1991) Crustal Structure of the Mamfe basin, West Africa, based on gravity data. Tectonophysics 186: 351-358.
- Manguelle-Dicoum E, Nouayou R, Tabod C, Kwende-Mbanwi TE (1999) Audio and Heliomagnetotelluric study of the Mamfe sedimentary basin. 58.
- Kangkolo R (2002) Aeromagnetic study of the Mamfe basalts of southwestern Cameroon. Journal of the Cameroon Academy of Sciences 2: 173-180.
- Eseme E, Agyingi CM, Foba-Tendo J (2002) Geochemistry and genesis of brine emanations from Cretaceous strata of the Mamfe Basin, Cameroon. Journal of African Earth Sciences 35: 467-476.
- Eseme E, Littke R, Agyingi CM (2006) Geochemical characterization of a Cretaceous black shale from the Mamfe Basin, Cameroon. Petroleum Geoscience 12: 69-74.
- Eseme E, Abanda PA, Agyingi CM, Foba-Tendo J, Hannigan RE (2006) Composition and applied sedimentology of salt from brines of the Mamfe Basin, Cameroon. Journal of Geochemical Exploration 91: 41-55.
- Nguimbous-Kouoh JJ (2003) Contribution of audio-magnetotelluric (AMT) for the subsurface layers study along the Manyu River. Masters thesis, Faculty of Sciences, University of Yaounde 1: 52.
- Eyong JT (2003) Litho - Biostratigraphy of the Mamfe Cretaceous Basin, SW Province of Cameroon-West Africa. PhD thesis, University of Leeds, 265.
- Ndougsa-Mbarga T (2004) Geophysical study by gravity method of the deep and superficial structures of the Mamfe region. Thesis of Doctorate, PhD, Fac, Sci, University of Yaounde 1, 255.
- Nouayou R (2005) Contribution of the Mamfe sedimentary basin geophysical study by audio and helio magnetotelluric prospecting. PhD thesis in the geophysics, University of Yaounde 1: 184.
- Ndougsa-Mbarga T, Manguelle-Dicoum E, Campos-Enriquez JO, Yene Atangana Q (2007) Gravity anomalies, sub-surface structure and oil and gas migration in the Mamfe, Cameroon-Nigeria, sedimentary basin. Geofísica Internacional 46: 129-139.
- Tabod CT, Tokam Kamga AP, Manguelle-Dicoum E, Nouayou R, Nguiya S (2008) An audio-magnetotelluric investigation of the eastern margin of the mamfe basin, Cameroon. The Abdus Salam International Centre for Theoretical Physics, Trieste, Italy.
- Ajonina HN, Ajibola OA, Bassey CE (2001) The Mamfe basin, SE Nigeria and SW Cameroon: A review of basin filling model and tectonic evolution. Journal of the Geosciences Society of Cameroon 1: 24-25.
- Ajonina HN, Betzler C, Jaramillo C (2010) Paleoclimatic significance of an Early Cretaceous fan-delta sedimentary succession in the eastern Mamfe Basin, SW Cameroon. 2010 Afrikagruppe deutscher Geowissenschaftler (AdG), Frankfurt, Germany, 30.
- Ajonina HN, Betzler C, Volkheimer W, Eyong JT (2008) Palynology and depositional environments of Early Cretaceous sediments in the Mamfe Basin, west Africa and their relationship to other Gondwanic regions in South America. 12th International Palynological Congress (IPC-XII) 8th International Organisation of Paleobotany Conference (IOPC), Bonn, Germany, 8.
- Ajonina HN, Betzler C, Eyong JT, Eseme E, Hell JV (2007) Stratigraphy and sedimentary evolution of the Mamfe Basin, southwest Cameroon, West Africa. 4th International Limnogeology Congress, Barcelona, Spain, 57.
- Ajonina HN, Njilah IK, Ndjeng E, Hell JV, Bassey CE, et al. (2006) Sedimentology and reservoir potential of sandstones of the Mamfe Formation, Mamfe Basin, southeast Nigeria and southwest Cameroon. Annales de la Faculté des Sciences Université de Yaoundé I, série Science de la Nature et de la vie, 36: 117-132.
- Ajonina HN, Jaramillo C, Volkheimer W, Mejía P, Betzler C, et al. (2010) Palynostratigraphy and age of the Lower Cretaceous Mamfe Group, Mamfe Basin, SW Cameroon, eastern West Africa. 8th European Palaeobotany-Palynology Conference (EPPC), Budapest, Hungary, 51-52.
- Ajonina HN, Betzler C, Hell JV, Eseme E, Volkheimer W, et al. (2012) Hydrocarbon potential of the Mamfe Basin, SW Cameroon. GV & Sediment Meeting 2012, Hamburg, Germany 31.
- Eyong JT, Wignall P, Fantong WY, Best J, Hell JV (2013) Paragenetic sequences of carbonate and sulphide minerals of the Mamfe Basin (Cameroon): Indicators of palaeo-fluids, palaeo-oxygen levels and diagenetic zones. Journal of African Earth Sciences 86: 25-44.
- Tikhonov AN (1950) On determining electric characteristics of the deep layers of the earth's crust. Dokl Akad Nauk SSSR 73: 295-297.
- Cagniard L (1953) Basic theory of the magneto-telluric method in geophysical prospecting. Geophysics 8: 605-635.
- Vozoff K (1991) The magnetotelluric method. In: MN Nabighian, Electromagnetic methods in applied geophysics. Society of Exploration Geophysicists, Tulsa, Oklahoma, 2: 641-711.
- Bastani M (2001) EnviroMT New Controlled Source/Radio Magnetotelluric. Ph.D. thesis, Uppsala University.
- Bastani M, Pedersen L (2001) Estimation of the magnetotelluric transfer functions from radio transmitters. Geophysics 66: 1038-1051.
- Garcia X, Jones AG (2005) A new methodology for the acquisition and processing of audio-magnetotelluric (AMT) data in the dead band. Geophysics 70: 119-126.
- Pratt J, Craven J (2010) Magnetotelluric imaging of the Nachako basin, Bristish Colombia. Geological survey of Canada.
- Dupis A (1970) First application of magnetotellurics to oil, geological and mining prospecting of various metropolitan regions. State-Doctorate ès-sciences.
- Benderritter Y (1982) Interpretation of magnetotelluric measurements using an ECA resistivity meter. Geophysical Research Center-Garchy-Nievre.
- Andrieux P (1987) Application of Magnetotelluric surveys to medium and deep exploration. U.P.M.C, Paris VI.
- Roger Guerin (2004) Synthesis of the research presented for obtaining the authority to direct research. 200.
- Pedersen L, Engels M (2005) Routine 2D inversion of magnetotelluric data using the determinant of the impedance tensor. Geophysics 70: 33-41.
- Marescot L, Loke MH, Chapellier D, Delaloye R, Lambiel C, et al. (2003) Assessing reliability of 2D resistivity imaging in mountain permafrost studies using the depth of investigation index method. Near Surface Geophysics 1: 55-67.
- Hjärten M (2007) Master thesis in interpretation of controlled-sourceradiomagnetotelluric data from Hallandsåsen. Uppsala Universitet Institution Enför Geovetenskaper, Geofysik, 120.
- Telford WM, Geldart LP, Sheriff RE (1990) Applied Geophysics second edition.
- Manguelle-Dicoum E, Nouayou R, Bokosah AS, Kwende-Mbanwi TE (1993) Audiomagnetotellurics soundings on the basement-sedimentary transition zone around the eastern margin of the Douala Basin in Cameroon. Journal of African Earth Sciences (and the Middle East) 17: 487-496.
- Avbovbo AA (1980) Basement geology in the sedimentary basins of Nigeria. Geology 8: 323-327.
Author Details
Jean Jacques Nguimbous-Kouoh1*, Theophile Ndougsa Mbarga2 and Eliezer Manguelle-Dicoum3
1Department of Mines, University of Maroua, Cameroon
2Department of Physics, University of Yaoundé, Cameroon
3Department of Physics, University of Yaoundé, Cameroon
Corresponding author
Jean Jacques Nguimbous-Kouoh, Department of Mines, Petroleum, Gas and Water Resources Exploration, Faculty of Mines and Petroleum Industries, University of Maroua, PO Box: 08 Kaele, Cameroon.
Accepted: July 04, 2018 | Published Online: July 06, 2018
Citation: Nguimbous-Kouoh JJ, Ndougsa-Mbarga T, Manguelle-Dicoum E (2018) Audio-Frequency Magnetotelluric Prospecting in the Mamfe Sedimentary Basin of Southwestern Cameroon. Int J Earth Sci Geophys 4:020.
Copyright: © 2018 Nguimbous-Kouoh, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The Audio-Magnetotellurics (AMT) method was used to study the heterogeneity level of shallow geological strata along a 36.6 km profile by different audio-frequency magnetotelluric techniques in the Mamfe sedimentary basin of southwestern Cameroon. The aim was to present the geoelectric structure of part of the southern section of the basin. The subsurface electrical anisotropy model was computed and showed anisotropy coefficient which varies between 0.7% and 2.6% indicating a degree of cracking less than 1 mm. The apparent resistivity profiles and pseudo-sections of transverse electric (TE) and transverse magnetic (TM) modes were computed and helped to highlight various electrical discontinuities in the basement and a multiplicity of heterogeneous layers. The subsurface geoelectrical model was performed and showed horizontal and vertical distribution of average electrical resistivities of layers that varies between 1 and 144 Ohm-m, at the depth greater than 2500 m. This model has highlighted three major discontinuities across the profile associated with superficial flaws. A vertical contact sediment/basement was found between Baku and Eshobi and was associated with a southeast edge of the Mamfe basin.
Keywords
Mamfe sedimentary basin, Audio frequency, Anisotropy, Apparent resistivity pseudo-section, Geoelectric model
Introduction
Over the past three decades, and particularly over the intervals 1985-1995 and 2005-2010, magnetotellurics has undergone a revolution driven by four main factors: (1) The emergence of low-power, low-cost, 24-bit digital electromagnetic sensing and recording technologies, (2) Dramatic improvements in the understanding of noise in electromagnetic measurements, with the concomitant evolution of data processing algorithms, (3) Substantial advances ability to recognize and remove distortion by near surface structure local to the measurement point that is the base of practical magnetotellurics, and (4) The development of fast two-and three-dimensional (2D and 3D) modeling and inversion capabilities concurrent with the constantly increasing power of computers [1]. In the 1970s, a typical magnetotelluric survey consisted of a handful of sites whose data were analyzed using ordinary least-squares methods, smoothed in the frequency domain to reduce data scatter, and interpreted using one-dimensional (1D) models "stitched" together into a 2D pseudo-section that may, or may not, be tested through 2D forward modeling [1]. By the 1990s, surveys comprising several tens of sites along a single line were common, data were processed using robust methods, which produced substantially more reliable response estimates that were subsequently analyzed for galvanic distortion, and rapid 2D modeling and inversion were standard [1]. By the 2010s, magnetotelluric surveys consisting of many hundreds of sites, with areal rather than linear coverage, are being carried out, data processing is semi-automatic, usually using bounded influence or multivariate approaches, multi-site distortion removal is being applied routinely, 2D interpretation, often including anisotropy, is routine [1].
The Audio-frequencies magnetotelluric (AMT) used from the context of this study is a variant of magnetotelluric. This method was conducted in the southern area of the Mamfe basin which is located about 150 km to the northeast of the meeting point of the early Cretaceous Benue Trough-Equatorial Atlantic-South Atlantic rift system triple junction. The Mamfe sedimentary basin is difficult to access due to its rugged terrain and the vast vegetation that hides most of the major geological structures and formations. Several previous studies have been carried out on the Mamfe sedimentary basin from the multidisciplinary framework [2-25].
Our study is part of the work of Nguimbous-Kouoh [12], in the southern area of the Mamfe basin. It is motivated by the need to significantly increase the geophysical knowledge of the basin. Its aims are to identify the geological strata heterogeneity, to estimate the degree of shallow layers cracking, and to propose the subsurface geoelectric structure of the southern area of the Mamfe sedimentary basin.
A discussion is conducted to assess the validity of the AMT method used in this study; the correlation between this study and some previous studies in the basin are discussed and suggestions are made for a more detailed study of the basin in light of finding commercial accumulations of hydrocarbons.
Geology of Study Area
The Mamfe sedimentary basin is an intracratonique rift basin formed in response to the dislocation of the Gondwana supercontinent and following the separation of South American and African plates. The basin is a small extension of the Benue sedimentary basin (Figure 1a). The basin is favorable to the exploration and exploitation of salt springs, minerals, precious stones and hydrocarbons. It has an area of approximately 2400 km2 and is located between latitudes 5°30'N and 6°00'N and longitudes 8°50' and 9°40'E (Figure 1b). It has the form of a plain with an average altitude that varies between 90 and 300 m above the sea level. Its average crustal thickness is between 33 and 40 km and the coat is at a depth of about 57 km [2-25].
Figure 1b shows the available geological map of the basin. Some geological details were extrapolated or removed. The geological map is preliminary and has jointly been updated following several studies. The geomorphology of the area is characterized by a succession of horst and grabens. Overall, the Mamfe sedimentary basin has a NW-SE structural trend with a length of 130 kilometers and a width of approximately 60 kilometers. It is bordered by faults, lineaments and rivers such as Manyu, Munaya and extends from Cameroon to Nigeria [2-25]. Lithologically, the basin is formed by thick Cretaceous age sediments whose thickness can vary according to the study site. It rests on granite-gneissic bedrock of Precambrian age. The order of the geological formations, from bottom to top, has a succession of granite, shale, sandstone, clays and laterite. The lamination forms a typical sigmoid syncline structure which is oriented E-W and plunge axes of 10° to about 20° W.
The tectonic history of the basin highlights the structures and syn-to post-sedimentary which has two main phases [2-25]:
• An expansion phase characterized by sedimentation.
• A compression phase during which sedimentation ended and the basin was closed.
The compression phase resulted in the creation of anticlinal and synclinal structures, horst and grabens deeding NW-SE. The phase of sedimentation and extension resulted in the creation of faults and syn-sedimentary folds.
The Magnetotelluric Method
The magnetotelluric (MT) method is a passive surface measurement of the earth's natural electrical (E) field and magnetic (H) field in orthogonal directions. It can be shown that the relationship between the horizontal orthogonal magnetic and electric fields depend on the subsurface resistivity structure. It is therefore used to determine the conductivity (resistivity) of the earth, ranging from a few tens of meters to several hundreds of kilometers. The fundamental theory was first developed by Tikhonov and Cagniard [26,27]. MT generally refers to recording of 10 kHz to 1000 s (0.001 Hz) or as low as 10.000 s (0.0001 Hz). AMT (audio MT) refers to audio frequencies, generally recording 100 Hz to 10 kHz. LMT-Long period MT generally refers to recording from 1.000 s to 10.000 s or much higher (to 100.000). The depth of penetration of MT soundings depends on the frequency, the lower the frequency the greater the depth of penetration and vice versa. The earth's electromagnetic field contains a wide spectrum (Figure 2). The low frequencies are generated by ionospheric and magnetospheric currents caused by solar wind (plasma) interfering with the earth's magnetic field. Higher frequencies (< 1 Hz) are due to thunderstorms near equator distributed as guided waves between the earth and the ionosphere. The time varying magnetic field induces electric field and hence currents in the ground. By measuring variations in the magnetic and electric fields in the surface of the ground, information on the subsurface resistivity can be obtained.
The sunspot cycle has been measured since the mid 17th century. There is a regular cycle of little over 10 years. Presently there is a minimum of activity (Figure 3), making MT soundings difficult in present years.
A typical setup for an MT sounding is shown in Figure 4. The horizontal orthogonal magnetic field, Hx (usually aligned in the magnetic north-south direction) and Hy (perpendicular to Hx) and the vertical magnetic field Hz are measured by magnetic coils. The horizontal orthogonal electric field, Expand Ey is measured by a pair of electrodes (the potential difference divided by the distance, 50-100 m). A GPS unit is used for synchronizing the data. The digital recording of the electromagnetic fields as a function of time is done through an acquisition unit and the time series saved on a memory card. The time series are Fourier transformed from the time domain to the frequency domain and processed. The tensors and the consequent apparent resistivity and phase are calculated as a function of the frequencies for later to be interpreted into a resistivity model of the subsurface.
General theory of magnetotelluric
The magnetotelluric methods use the four Maxwell's equations which describe the electromagnetic field. They are Gauss's law for the magnetic field (divB = 0) and Gauss's law for the electric field (divD = q) Faradays's law and Ampère's law with Maxwell's term:
: Electric field intensity (V/m); : Magnetic field intensity (A/m); : Electrical current density ; : Conductivity (Siemens/m) ; : Electrical permittivity; μ: Magnetic permeability.
Assuming: Harmonic dependence of the oscillating electromagnetic fields: ; : Angular frequency; T: period; gives: ; vertical incident plane wave: .
Using Faraday's law above, gives:
Similarly applying Ampère's law above gives:
Combining Faraday's and Ampère's law gives:
For the quasi-stationary approximation:
And
This can be written:
The general solutions for a homogeneous earth (σ constant) can be written as:
Axy; Bxy are constants to be determined
As and ; and we get:
The impedance tensor elements Zij are defined as:
And we can calculate the resistivity of the half-space
The resistivity may also be written as:
For a non-homogeneous earth the apparent resistivity (ρa) and phase are defined as:
Z0 is impedance at surface.
The depth of investigation, also called the skin depth can be estimated by the following expression: [28-30]. In this formula T is the period of the propagating signal.
The general definition of the impedance tensor is:
For 1D earth, Zxx = Zyy = 0 and Zxy = -Zyx.
For 2D earth is possible to rotate the tensor in the strike direction and Zxx = Zyy = 0.
For 3D earth it is not possible to rotate the tensor and get Zxx = Zyy = 0.
The magnetotelluric method is well documented in the literature [28-32].
Audio magnetotelluric data
The data used for this study were collected using the resistivity-meter LAGAS of the Garchy laboratory in France. A line containing 6 AMT stations was used with frequencies ranging between 3-2500 Hz. The geographical coordinates of the line can be found in Figure 1b and Table 1 [12,15]. The profile is approximately 36.6 kilometers and is oriented approximately NW-SE. The location of stations and the direction of the line were obtained using a compass and a GPS. The electrodes were deployed at each station, using two electrodes on the north-south direction and two on the east-west direction. The length of the telluric line was set to 100 m on both directions. The names of the stations were selected such that they correspond to the localities; we have: Ndwap (M1), Abonando (M2) Esagem1 (M3), Esagem2 (M4), Baku (M5) and Eshobi (M6) (Figure 1b). The processing of the data consisted in spectral analysis and manual editing for the removal of noisy data. The inversion of the data was done with the software [33-35]. The anisotropy coefficients were calculated using the formula . The mean apparent electrical resistivities at each frequency were calculated using the following formula .
Structural Interpretation
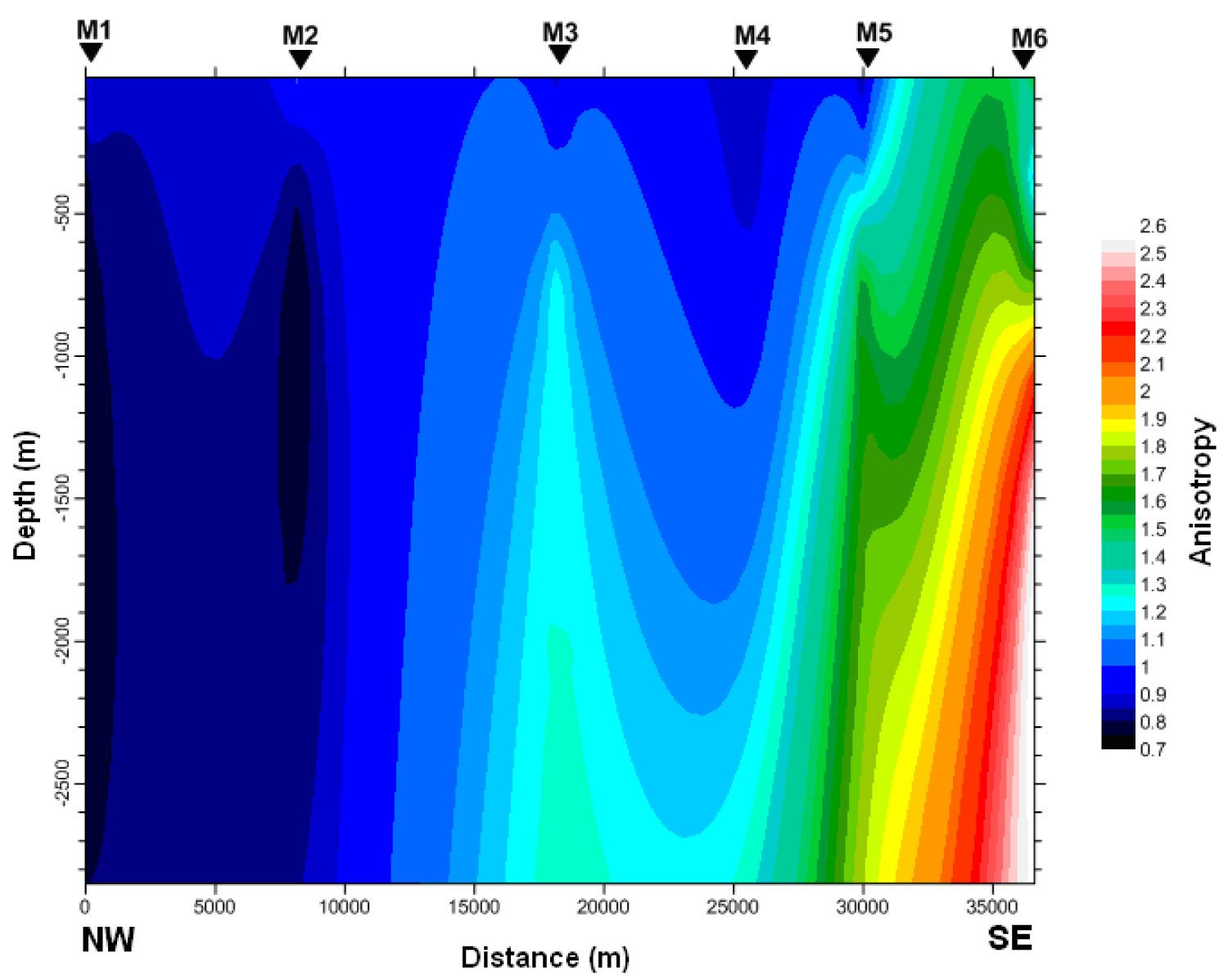
The visualization of the heterogeneity effects and the structural interpretation were done using the result from the anisotropy profile (Figure 5), the mono-frequency profiles (Figure 6), the pseudo-sections (Figure 7) and the geoelectric model (Figure 8).
Profile of anisotropy
The two resistivities and are not equal and the electrical resistivity structure is 1D. The coefficients of anisotropy are used to settle the 1D assumption, to test the data quality and to determine the degree of subsurface cracking [35,36]. Here we want to evaluate the variability of the coefficient of anisotropy, to identify the heterogeneity of strata and estimate the degree of underground cracking.
Figure 5 is a reproduction of the underground electric distribution of apparent anisotropy coefficients along the profile. High or low anisotropy values are observed at different depths. The electrical anisotropy coefficients are represented by different colors and their values vary between 0.7% and 2.6%. The blue and black colors match the signature of the geological layers of low and medium anisotropy. These layers can be associated with some heterogeneous layers while the green colors, red and yellow are the signature of geological layers of high anisotropy. They may correspond to highly heterogeneous layers. The fact that the coefficient of anisotropy varies between 0.7% and 2.6% is evidence of little data dispersion between the telluric and magnetic direction. It is also evidence of a low degree of geological layers cracking.
Monofrequencies profiling
The profile of electrical resistivity allows the qualitative study of non-tabular structures. It helps highlighting the lateral distribution of apparent resistivity for each frequency.
Figures 6a and Figure 6b show the lateral variations of apparent resistivity for the twelve frequencies. The TE and TM modes are displayed such that, the distance between stations are plotted on the x-axis while the apparent resistivity in logarithmic scale is plotted on the y-axis. Overall, the two profiles of resistivity show areas of with relative conductive or resistant discontinuities. These discontinuities may represent faults or zones of contact between layers of different lithologies. The change in slope between different stations marks the change of geological strata. A gentle slope corresponds to a minor lithological change while an abrupt change in slope is associated with a significant lithological change between the stations.
Pseudo-sections of apparent resistivity
Figures 7a and Figure 7b show the response of the pseudo-sections in TE and TM modes. The interval between resistivity contours is the same in both modes. The label frequencies are two on the color scale. The pseudo-sections in TE and TM modes are displayed such that the distances between stations are plotted on the abscissa and the frequencies are plotted on the ordinate. Overall, the two pseudo-sections have electrical discontinuities or abnormalities that may be associated with underground geological structures. The resistivity following the N-S magnetic mode are high to low at high frequencies (1-260 ohm-m), while the resistivity on the TE mode (E-W) are relatively low (1-85 Ohm-m). This generally indicates that the telluric current meets a great resistance when passing through the geological layers in the magnetic direction N-S. The two pseudo-sections highlight two shallow discontinuities near the stations M2 and M4. They also allow locating a geometric boundary between the stations M5 and M6. This boundary may correspond to a zone of contact between two geological layers of different types. The electrical resistivities are represented by different colors just below the surface and at depth. The observation of the distribution of these colors on both pseudo-sections shows that the geological layers are more heterogeneous in the E-W direction than in the N-S direction.
Interpretation of the geoelectric model
The geoelectric model is a representation of the variation of the subsurface electrical resistivity with depth obtained after the inversion of processed field data. Generally, it is assumed that the resistivity do not change in the direction perpendicular to the profile. The starting model can be a homogeneous model or an estimated model obtained using a priori geological information. The final model obtained after the inversion generally requires several iterations and is non-unique. Additional information such as resistivity logs are necessary to constraint the inversion and obtain the best model. The final model can be represented using contour map of constant resistivity values [36-39].
The geoelectrical model of our profile is displayed in Figure 8. This model represents the vertical and horizontal distribution of underground average resistivity. The discontinuities depth and prospected layers is greater than 2500 m. The contour curves are such that, by reducing the interval between the resistivity we manage to combine low-contrast geological layers; which allows to observe the major discontinuities. When the intervals between the resistivities are very large, layers of different resistivity values are highly fragmented, and do not allow precise location of discontinuities. The model has different resistivity horizons: the low resistivity values (1-25 Ohm-m) can be associated with all the sedimentary rocks between station M1 and M5; while the high resistivity (26-144 Ohm-m) can be associated with relatively high resistivity rocks, probably the basement, between stations M5 and M6. The model has three shallow discontinuities near stations M2, M3 and M4. These three discontinuities may be associated with subterranean fractures. Whereas the corresponding limit to the discontinuity between M5 and M6 may be associated with a stepped hole; considering the difference in altitude (35 m) between the two stations (Table 1). This limit can also be associated with a vertical contact between sediments and basement rocks. It is substantially perpendicular to the profile.
Discussion
This study shows that the anisotropy in the area is related to shallow heterogeneities. This anisotropy may be associated with the occurrence of shallow scattered volcanic rocks from the Cameroon Volcanic line in the basin (Figure 1a and Figure 1b).
Roger Guerin [36] has shown that the scatters greater than 1 mm are detectable for values of anisotropy coefficient lower than 0.42 or greater than 3.14. Similarly, when the anisotropy coefficient is greater than 1 (respectively less than 1) scatters are preferentially oriented at 0 degrees (respectively 90 degree) in the direction of the profile. Based on this result, we can conclude that the degree of scattering along the southern part of the basin is less than 1 millimeter and that the orientation of scatters is between 0 and 90 degrees.
Telford, et al. [40] demonstrated that the values of the anisotropy coefficient can be as large as 2 in some graphitic slates, and range from 1 to 1.2 in rocks such as limestone, shale and basalt. Manguelle-Dicoum, et al. [41] calculated the coefficients of anisotropy of various rocks collected in the Douala sedimentary basin; they demonstrated that the range of values 1.02 to 1.06 could be associated with intercalated shale with sandstone and/or thick sections of alluvium. Based on these assumptions, and considering that the Mamfe sedimentary basin and the Douala basin are two neighboring structures of the Benue trough, we can tentatively conclude that the rocks in the southern part of the basin are basalts, shales, sandstone and alluvium.
Correlations between this study and other geological, geochemical and geophysical observations in the field [10,11,17] allow us to say that the low resistivity values associated with volcanic and sedimentary rocks are probably due to the occurrence of shallow salt springs that are present at different locations in the basin or the presence of hydrocarbon.
The aeromagnetic study by Kangkolo [8] revealed the existence of mineralized zones at the boundaries between sediment and basalts in the south-eastern part of the basin. The contact zone sediment/basement identified between Baku and Eshobi can also be associated with a zone of mineralization.
The thickness of sediments obtained from this profile (> 2500 m) is relatively close to that obtained by Kangkolo [8] (2000 m) by spectral analysis and 2.5D modeling of aeromagnetic data of different profiles across two locations (Adjayoudip and Osing-Ikom) located above basaltic flows.
This study, and that by Nouayou [15] show that the audio-magnetotelluric method is effective in the study of the Mamfe basin to a maximum depth of approximately 2500 m. Imaging deeper structures will necessitate the use of frequencies (below 1 Hz).
Conclusion
The implementation of the audio-magnetotelluric method in the Mamfe sedimentary basin allowed us to explore the deep basin, to observe the horizontal and vertical variation of anisotropy coefficients and resistivity along the southern part of the Mamfe basin. The anisotropy model enabled to distinguish different heterogeneous areas of the profile. The pseudo-sections in telluric and magnetic modes allowed highlighting two major discontinuities and identifying the most heterogeneous layers in the E-W direction. The apparent geo-electric model allowed highlighting three major discontinuities that were associated with shallow faults or fractures. Based on this study and previous studies carried out on the basin, it would be interesting for future studies to improve knowledge of the basin using tensor decomposition to study the dimensionality and extract the 2D and 3D impedance tensor which should be corrected for static shift caused by shallow heterogeneities. A more complete study of the basin should be conducted with the contribution of other geophysical methods such as Helio-magnetotelluric and seismic.
Acknowledgments
We thank IRGM and SNH for the authorization to use the data set in this article.