
International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 3, Issue 1
Orginal Article
DOI: 10.35840/2631-5017/2509
Calculation of Silicon Plasmas with a Relativistic Collisional Radiative Average Atom Code
AJ Benita1,2*
Table of Content
Figures
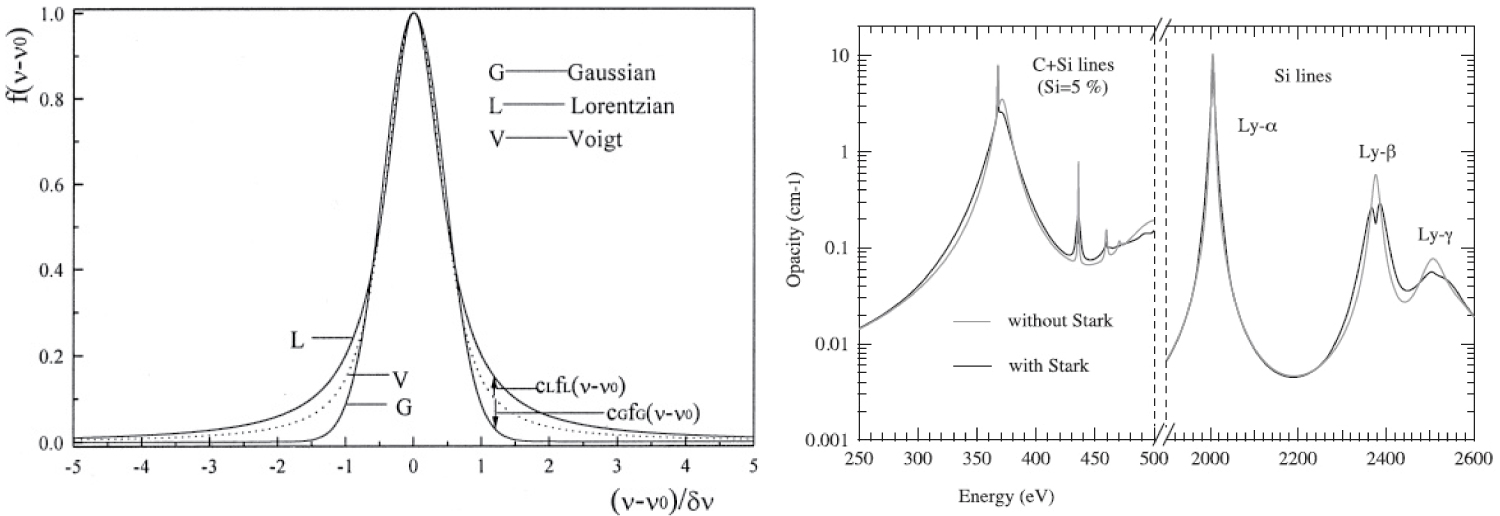
Figure 1: Typical Gaussian, Lorentzian and Voigt bound...
Typical Gaussian, Lorentzian and Voigt bound-bound line profiles (left). Opacity profiles with or without Stark broadening of plasma C + Si mixture at electronic density Ne = 6E + 23 cm-3, electronic temperature Te = 1000 eV. The fraction of silicon is 5%.
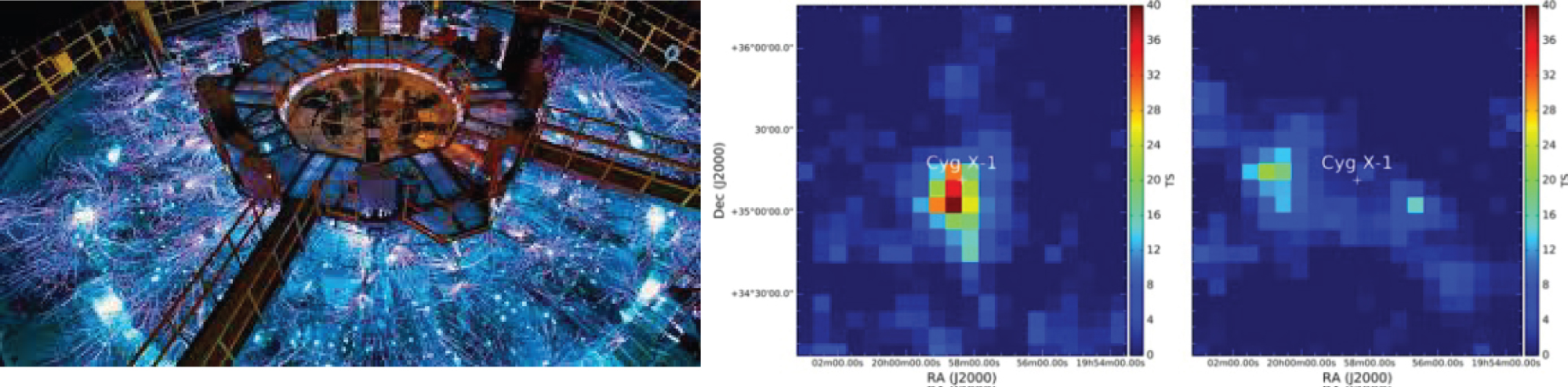
Figure 2: Sandia's Z-machine of 1.6 MJ X-ray burst with...
Sandia's Z-machine of 1.6 MJ X-ray burst with a 3 ns FWHM and 220 TW peak power (left). Detection of gamma rays of likely jet origin in Cygnus X-1 (right), which is a galactic X-ray source with accretion disk, compact object, companion star and blobs of plasma.
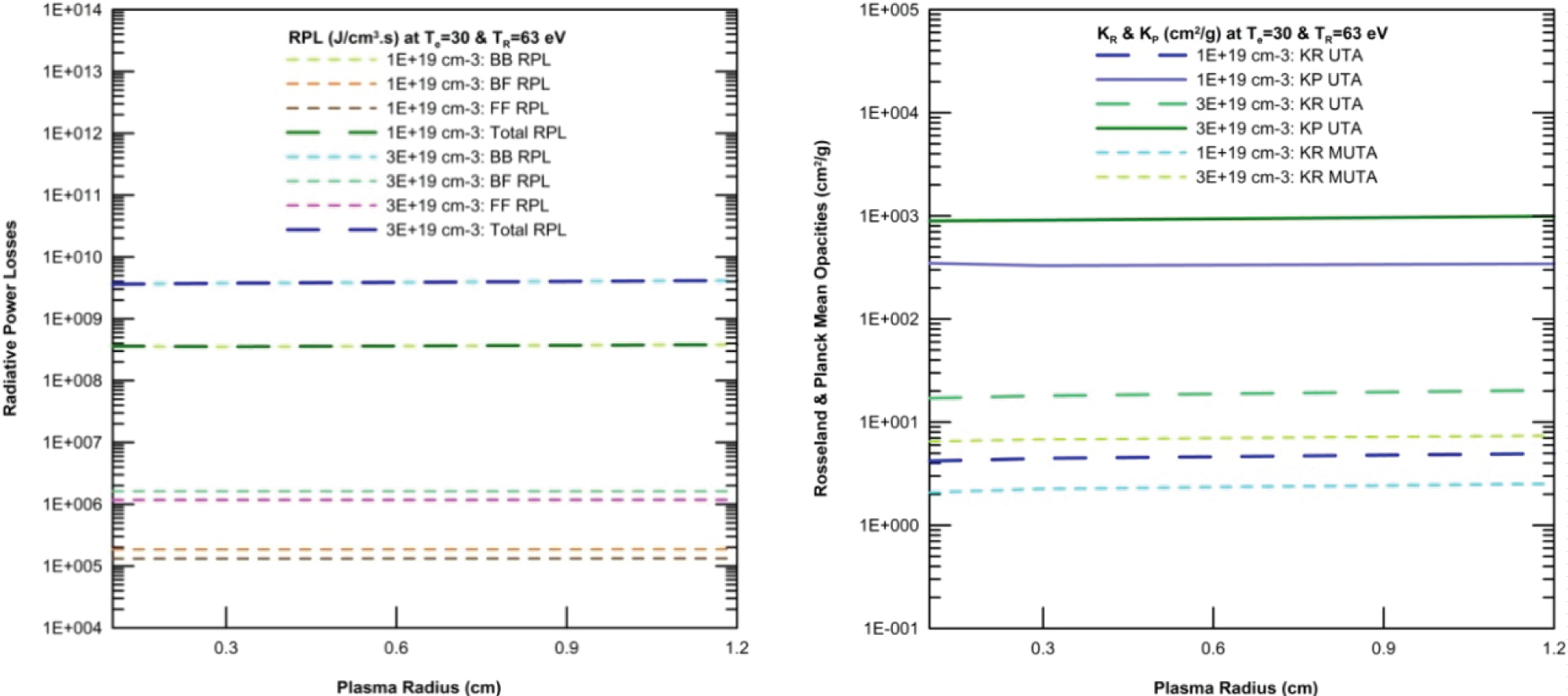
Figure 3: Radiative Power Losses and Mean opacities...
Radiative Power Losses and Mean opacities at Ne = 1E + 19/3E + 19 cm-3, Te = 30 eV, TR = 63 eV, Xdil = 1.0, plasma radius 0.1, 0.3, 1.2 cm.

Figure 4: Hohlraum and capsule for Inertial Confinement...
Hohlraum and capsule for Inertial Confinement with indirect drive approach and opacity (cm2/g) at Te = 300 eV for SiC, TR = 0 eV and Ne = 6.0E + 23 cm-3 with the code ALICE II [14] (lines as legend) and ATMED CR (orange line), the grey line belongs to the spectrum registered by DANTE (upper graphs). Opacity of mixtures of C + Si with percentage 1%-2%-3% Si calculated with Pim Pam Pum (PPP) code at density ρ = 0.01 g/cm3 and Te = TR = 50 eV and mixtures C + 1% Si at several densities [2,24] and profiles of ATMED CR (intermediate graphs). Opacity for the aforementioned mixtures calculated with ATMED CR code at several densities and % of Si at Te = TR = 50 eV and mean charge of SiO2 and 5% SiC mixtures in LTE or NLTE regimes with dilution factor 1 at Te = 200 ÷ 500 eV, TR = 300 eV and ρ = 2.6 g/cm3 (lower graphs).
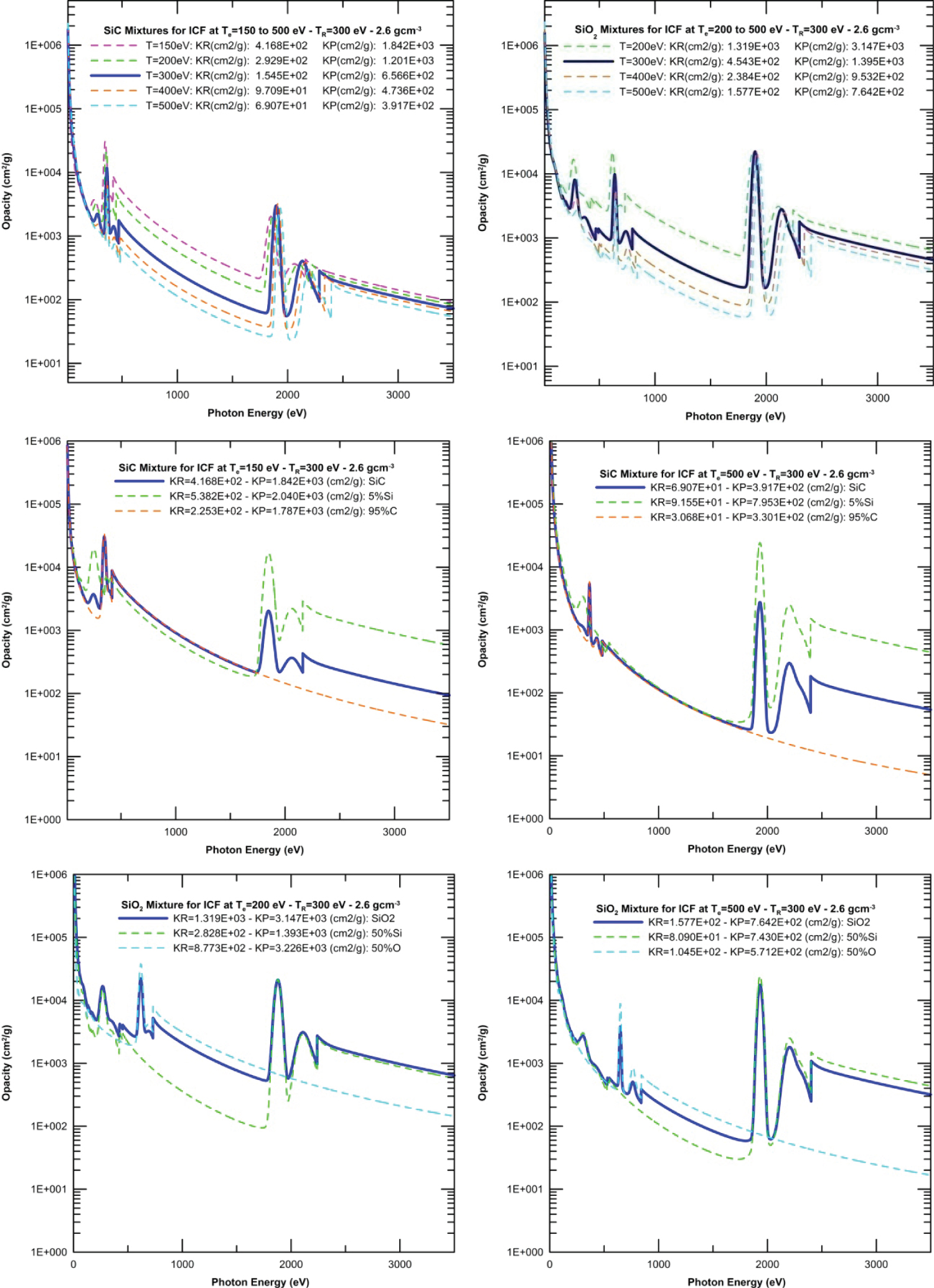
Figure 5: Spectrally resolved opacity (cm2/g)...
Spectrally resolved opacity (cm2/g) at several electronic temperatures and TR = 300 eV for SiC at Te = 150 ÷ 500 eV or SiO2 Te = 200 ÷ 500 eV and ρ = 2.6 g/cm3 (upper graphs). Spectrally resolved opacity (cm2/g) at TR = 300 eV for mixtures and components (dashed lines) at several electronic temperatures and 2.6 g/cm3: 5% SiC at Te = 150 eV; 5% SiC at Te = 500 eV; SiO2 at Te = 200 eV and SiO2 at Te = 500 eV.

Figure 6: Left plot showing calculation of...
Left plot showing calculation of the specific energy stored in the coronal plasma at 2 ns in the laser pulse of 635 kJ, for the XSN average atom model [8] and Detailed Configuration Accounting models which use a flux limit of 0.05 or 0.15 respectively. The spectrum at peak x-ray flux with a radiation temperature of 340 eV and a x-ray power of 19,600 GW/sr is included as measured by Dante (▬▬) and calculated spectrum using the DCA code (▬▬). Right plot showing Flux (GW/sr) and radiation temperature (eV) as seen by capsule and resulting from modulating the laser beam energy (kJ) incident over the hohlraum. Scaling of the (●) measured peak radiation fluxes compared with the ones of XSN simulation with a flux limit of 0.05 (▬ ▬) and of the DCA model with a flux limit of 0.15 (▬▬). The peak radiation measured temperatures (■) are displayed also along with a curve fit (•••••) at 2 ns and wall albedo of 90% inferred from simulation that gives ~88% of conversion efficiency.

Figure 7: Radiation temperature as seen by capsule versus time (ns)...
Radiation temperature as seen by capsule versus time (ns) [27]. Typical capsules for ICF with doped ablator with several fractions of silicon. Mean charge evolution Zbar (t) of capsule plasma CH + 2% Si. Opacity (cm2/g) at several temporal intervals of mixture. Opacity of mixture (solid lines) and components (dashed lines) at: 1.4E - 09 s and 2.0E - 09 at TR = 230 eV; 1.0E - 09 and 2.9E - 09 at TR = 170 eV.
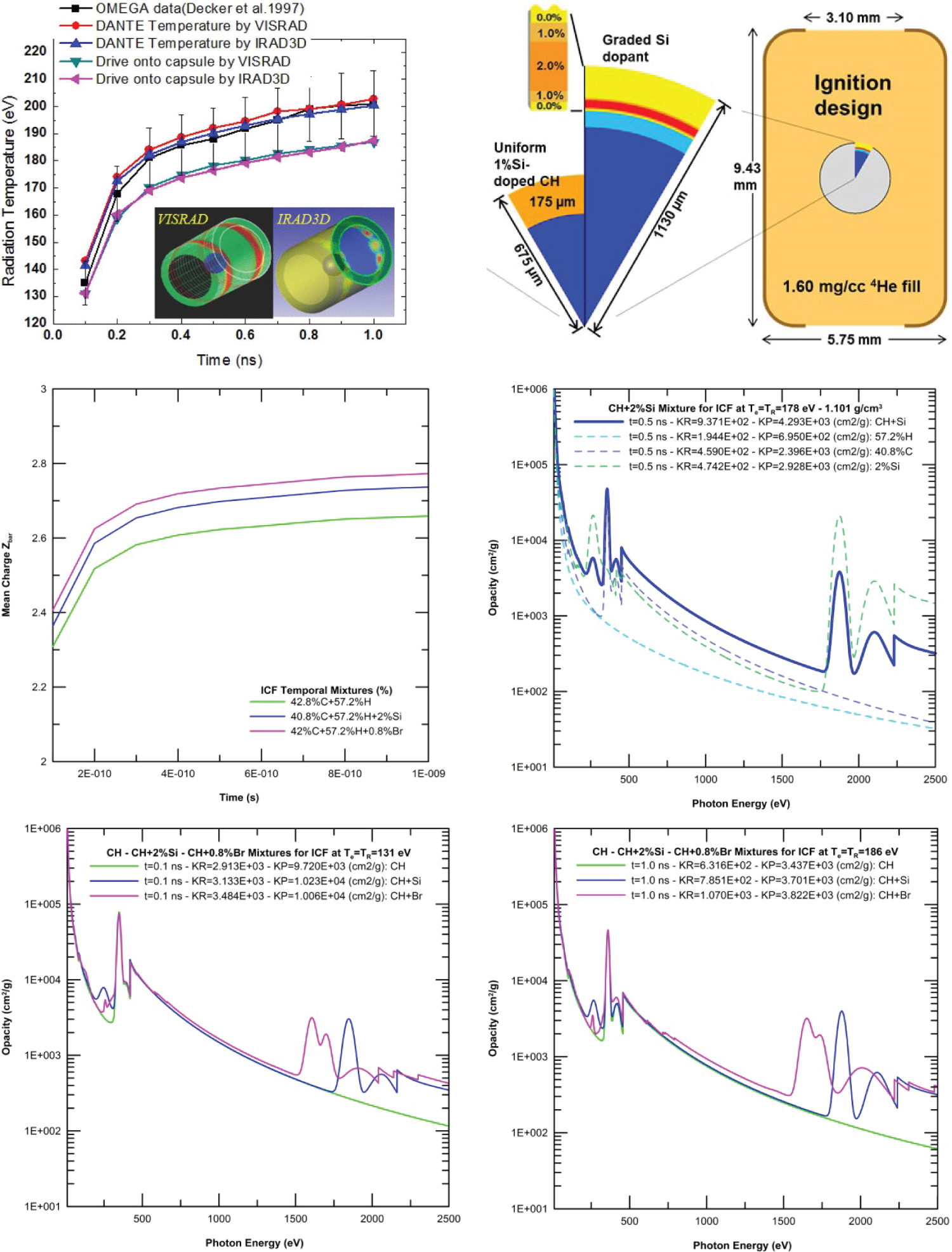
Figure 8: TR of capsule versus time (ns)...
TR of capsule versus time (ns). ICF capsules, the internal layers of ablator are graded doped with Si [28]. Mean charge evolution Zbar (t) of CH, CH + 2% Si, CH + 0.8% Br. Opacity (cm2/g) at several temporal intervals of mixtures (solid lines) and components (dashed lines).
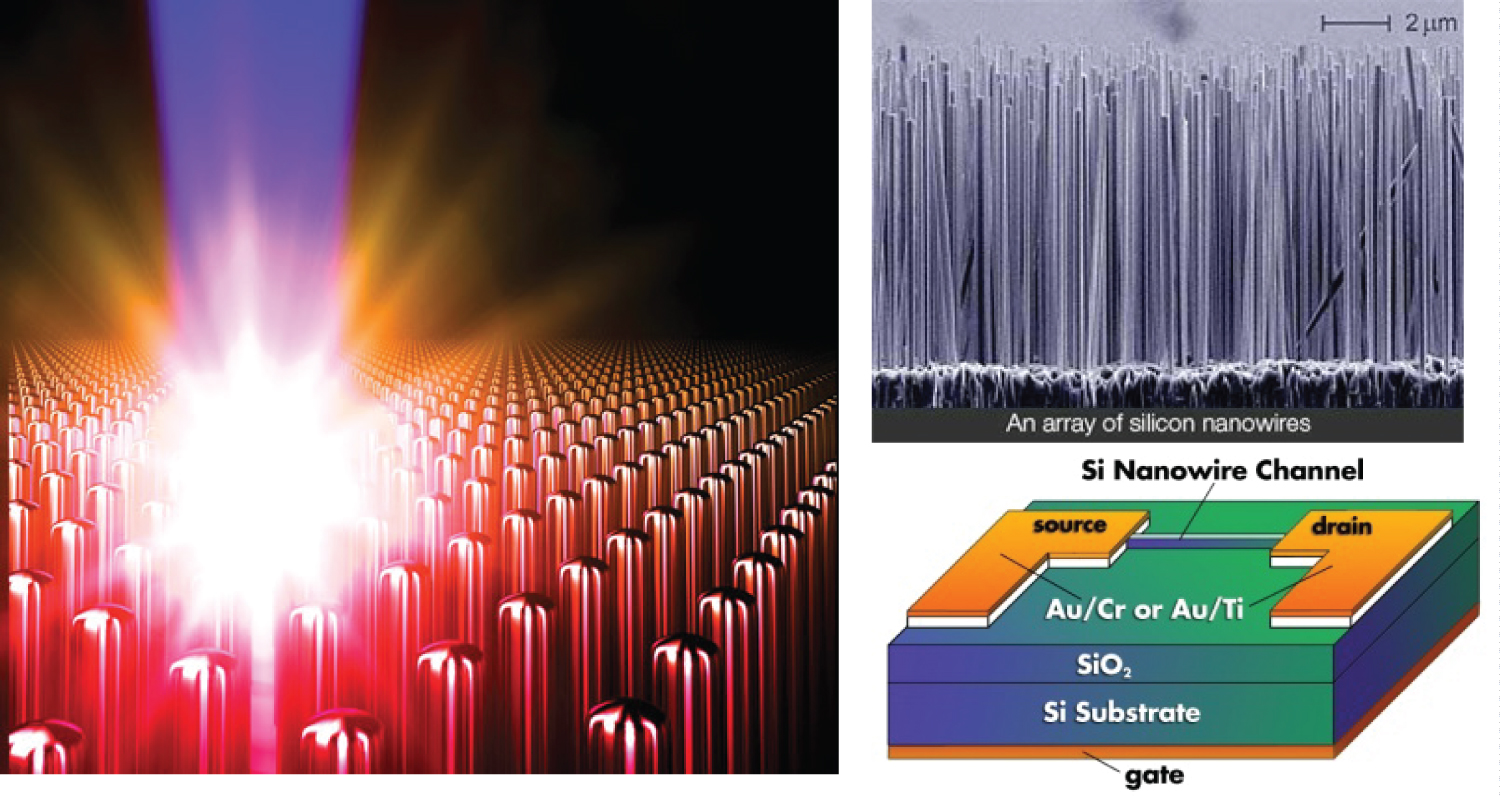
Figure 9: Irradiation of aligned nanowire arrays with...
Irradiation of aligned nanowire arrays with UHED regime for the study of atomic properties [20] (left). Array of silicon vertical nanowires and schematic diagram of the silicon nanowire channel for planar transistor of NIST on silicon substrate (right).

Figure 10: Matter density (g/cm3) inwards...
Matter density (g/cm3) inwards evolution versus time and position with the hydrodynamic code HYAT 1D + ATMED CR in instants 0.03, 0.1, 0.6, 1, 3, 5, 6 and 7 ns at conditions of case N1 in simulations of irradiated 25 μm silicon targets. Characterization of nanowires of silicon and titanium with lasers for irradiating targets (upper graphs). Matter density, electronic and ionic temperatures (eV) at times 0.03 ns and 6 ns versus position with heat wave propagation from the irradiated side outwards the silicon target (lower graphs).
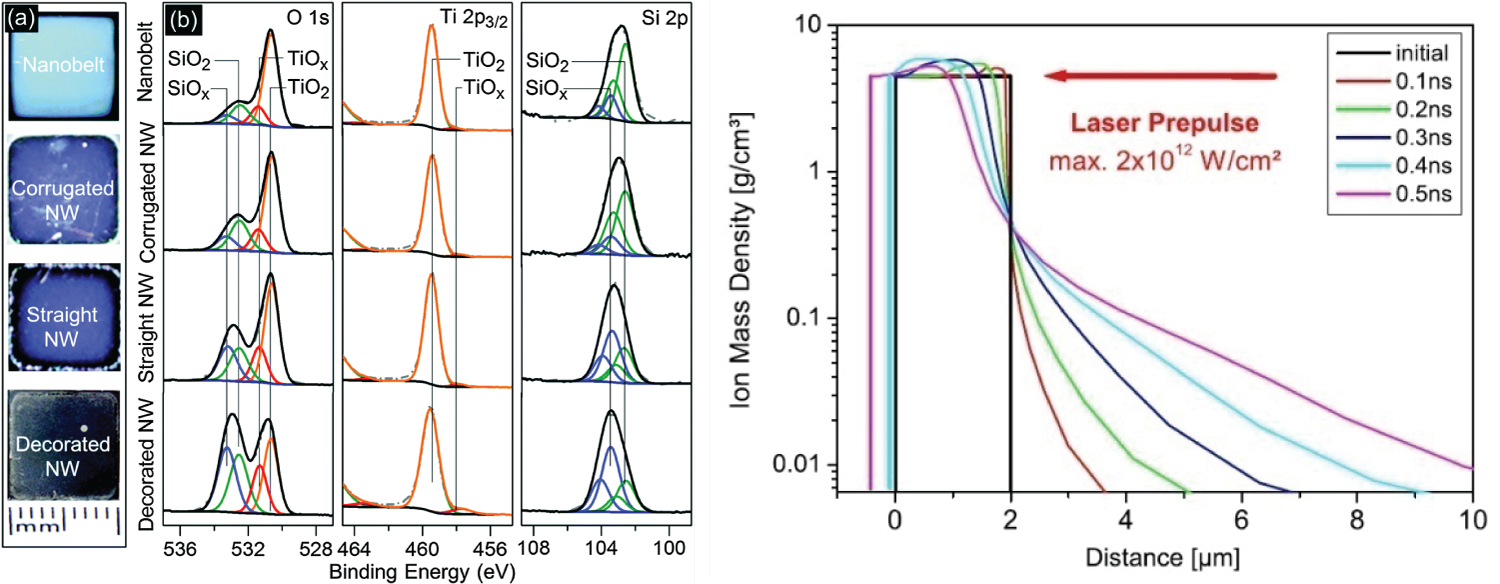
Figure 11: Characterization of nanowires of silicon...
Characterization of nanowires of silicon and titanium with lasers for irradiating targets (left). Matter density vs. time and position with code HELIOS 1D in instants 0.1, 0.2, 0.3, 0.4 and 0.5 ns of foils of 2 μm Ti [34] with a laser peak intensity 2 × 1012 W/cm2 (right).
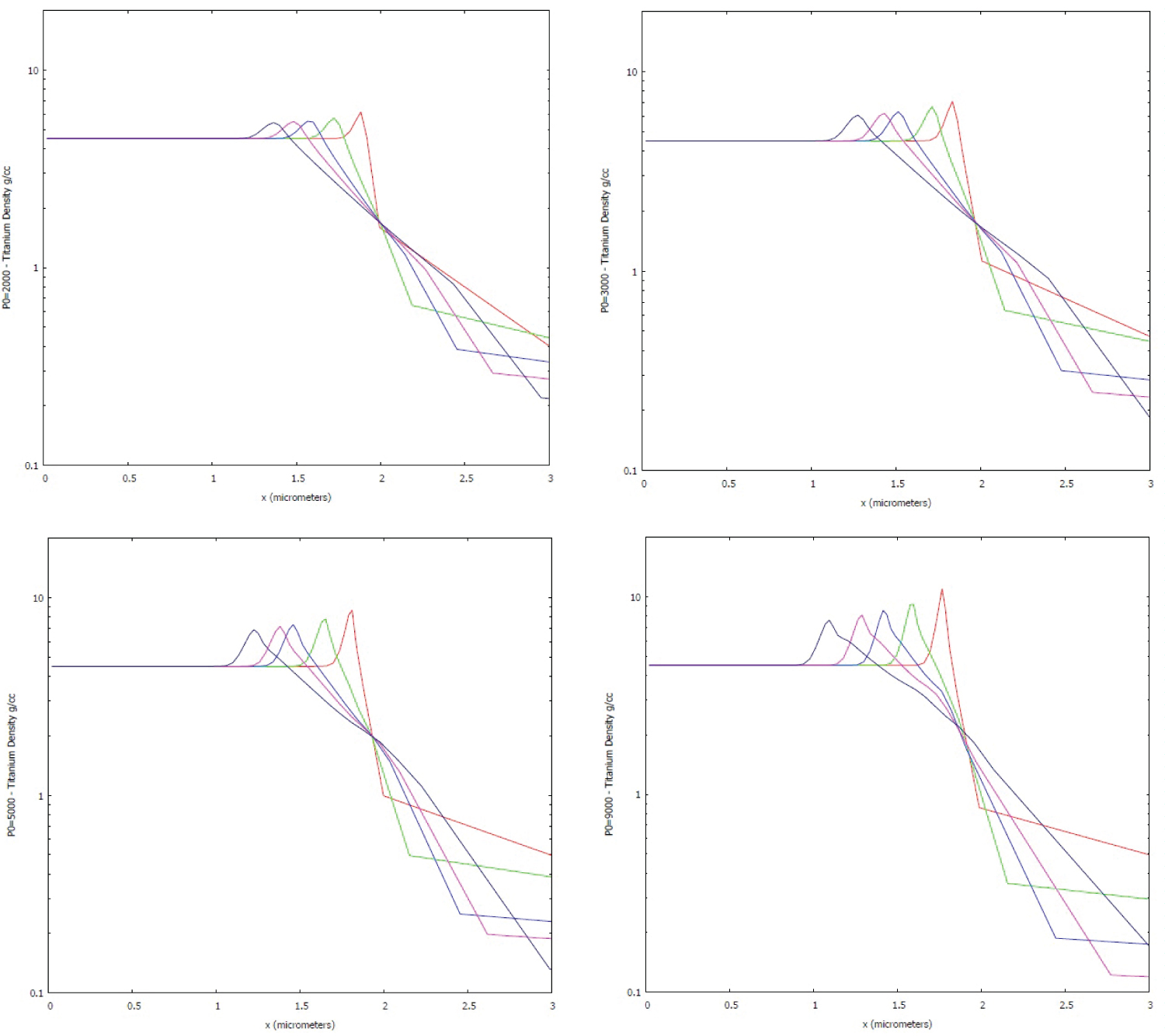
Figure 12: Matter density (g/cm3) inwards...
Matter density (g/cm3) inwards evolution versus time and position with the hydrodynamic code HYAT 1D + ATMED CR in instants 0.1, 0.2, 0.3, 0.4 and 0.5 ns at conditions of several values of maximum peak of laser pulse P0 of irradiated 2 μm titanium targets.
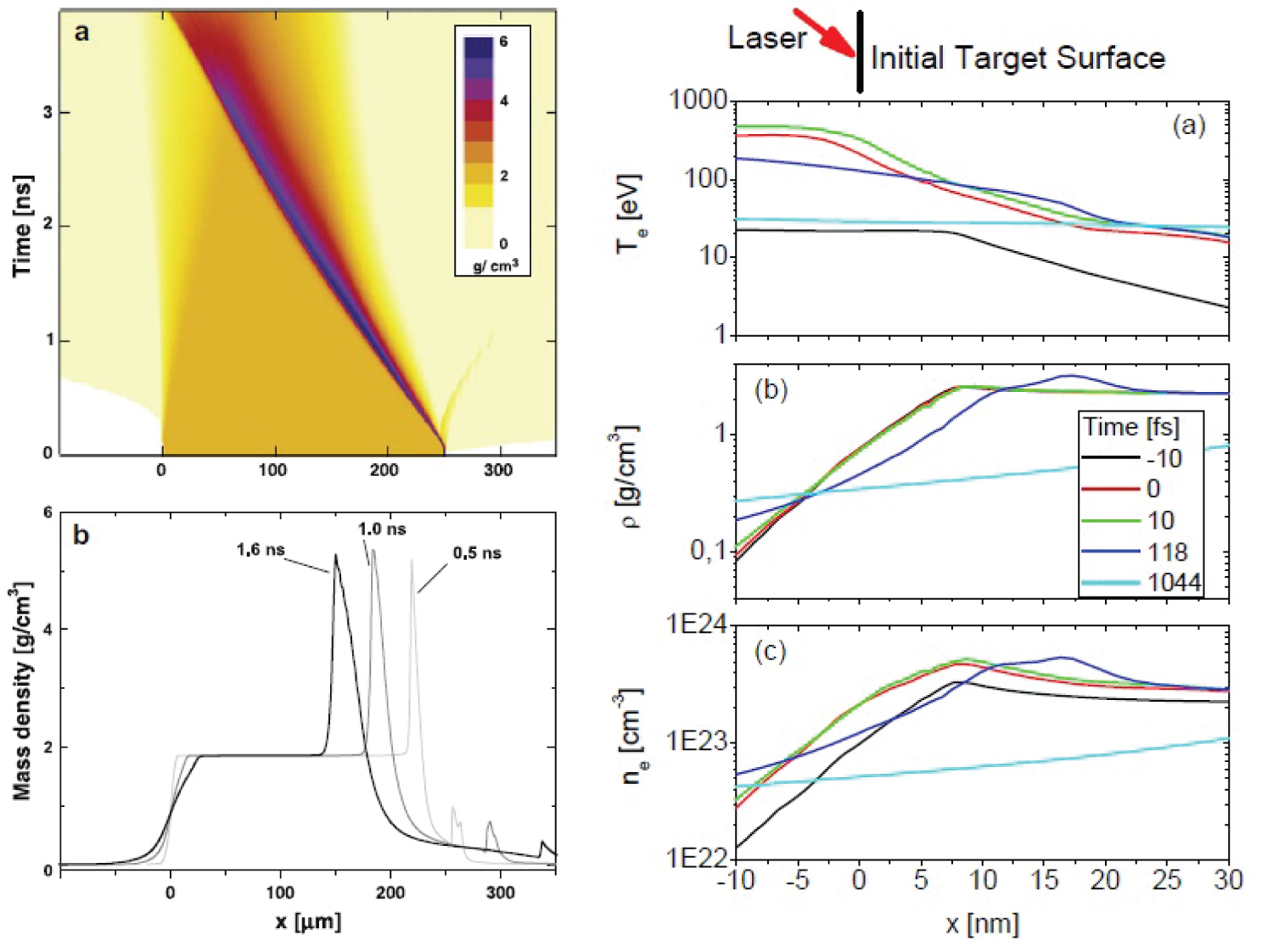
Figure 13: Matter density vs. time and position with HELIOS...
Matter density vs. time and position with HELIOS 1D of beryllium foils of 250 μm [35] (left) and with one dimensional Lagrangian hydrocode MULTI-fs + FLY 1D of carbon targets of 30 nm [43] with initial position of surface at x = 0 and peak intensity 3 × 1016 W/cm2 (right).
Tables
Table 1: Main parameters of Sandia's Z-Machine experiments of optically thick plasmas of silicon [21,22].
Table 2: Mean charge of optically thick plasmas of silicon with Planckian fields calculated with ATMED CR.
Table 3: Mean charge of optically thick plasmas with 1, 2 or 3 Planckian fields calculated with ATMED CR.
Table 4: Rates out/into all energy levels (Σ Pnlj) of silicon plasmas proposed in the Workshop NLTE-10, considering for photoionized plasmas as electronic temperature Te = 30 eV.
Table 5A: Ranges and main parameters used in simulations of plasmas of silicon created from exploding nanowires with FLFT = 0.1.
Table 5B: Evolution of variables with HYAT + ATMED CR of 25/50 μm silicon plasmas at several coordinates x (μm) and instants, including the last cell affected by the irradiation before the first non-perturbed one (2.330 g/cm3) and cells inside/outside the target on laser irradiated side, observing a heat wave propagation from the irradiated side outwards the Si target with time progression as in Figure 10.
Table 6A: Evolution of variables with HYAT + ATMED CR of 2 μm Ti plasmas with P0 = 2000 for several coordinates x (μm) and instants, including the last cell affected by the irradiation before the first non-perturbed one (4.5070 g/cm3) in the material, the cell of a peak in density, two intermediate ones and the first cell affected of target on laser irradiated side, giving way to a similar parabolic evolution of mass density as equal as in HELIOS 1D, Figures 11 and Figure 12.
Table 6B: Evolution of variables of 2 μm Ti plasmas with P0 = 1000 ÷ 9000 for the coordinate of the cell of a peak in density and instants.
Table 6C: Evolution of variables with P0 = 9000 of 2 μm Ti plasmas for several coordinates x (μm) and instants, including the last cell affected by the irradiation before the first non-perturbed one (4.5070 g/cm3) in the material, the cell of a peak in density, two intermediate ones and the first cell affected of target on laser irradiated side, giving way to a peaked profile evolution of mass density.
Table 6D: Density peak of 2 μm titanium plasmas for several instants computed with HYAT (Z) or with HYAT + ATMED (Zbar).
References
- AJ Benita, E Mínguez, MA Mendoza, JG Rubiano, JM Gil, et al. (2015) Collisional radiative average atom code based on a relativistic screened hydrogenic model. High Energy Density Physics 14: 18-29.
- AJ Benita (2017) Collisional radiative average atom code with relativistic atomic model. Theoretical physics LAP Lambert Academic Publishing.
- AJ Benita (2012) Fast Calculation of Plasmas Properties with ATMED LTE. Project of Nuclear Science and Technology Master at UPM.
- MA Mendoza, JG Rubiano, JM Gil, R Rodriguez, R Florido, et al. (2013) Fast Computation of radiative properties and EOS of warm dense matter using the ATMED code. Eight International Conference on Inertial Fusion Sciences and Applications (IFSA 2013).
- MA Mendoza, JG Rubiano, JM Gil, R Rodriguez, R Florido, et al. (2014) Calculation of radiative opacity of plasma mixtures using a relativistic screened hydrogenic model. Journal of Quantitative Spectroscopy & Radiative Transfer 140: 81-98.
- MA Mendoza, JG Rubiano, JM Gil, R Rodriguez, R Florido, et al. (2011) A new set of relativistic screening constants for the screened hydrogenic model. High Energy Density Physics 7: 169-179.
- FH Ruano, JG Rubiano, MA Mendoza, JM Gil, R Rodriguez, et al. (2012) Relativistic screened hydrogenic radial integrals. Journal of Quantitative Spectroscopy & Radiative Transfer 117123-117132.
- WA Lokke, WH Grasberger (1977) XSNQ-U A Non-LTE emission and absorption coefficient subroutine. Prepared for U.S. Energy Research & Development Administration under contract No. W-7405-Eng-48, UCRL-52276.
- G Faussurier, C Blancard, T Kato, R More (2009) Prigogine theorem of minimum entropy production applied to the average atom model. High Energy Density Physics 5: 283.
- Balazs F Rozsnyai (2010) Hot plasma opacities in the presence or absence of local thermodynamic equilibrium. High Energy Density Physics 6: 345-355.
- Balazs F Rozsnyai (1997) Collisional radiative average atom model for hot plasmas. Physical Review E 55.
- RC Mancini, IM Hall, T Durmaz, JE Bailey, GA Rochau, et al. (2010) Experiments and modeling of photoionized plasmas at z. Science with High-Power Lasers and Pulsed Power Workshop, August 4-6, Santa Fe, NM.
- PAM Van Hoof, ME Foord, RF Heeter, JE Bailey, HK Chung, et al. (2005) Modeling x-ray photoionized plasmas produced at the Sandia Z-facility. Astrophysics and Space Science 298: 147-153.
- EG Hill, SJ Rose (2012) Modelling of silicon in inertial confinement fusion conditions. High Energy Density Physics 8: 307-312.
- WU Ze-Qing, HAN Guo-Xing, PANG Jin-Qiao (2002) Opacity calculations for non-local thermodynamic equilibrium mixtures. Chin Phys Lett 19: 518.
- MacFarlane JJ, Golovkin IE, Mancini RC, Welser LA, Bailey JE, et al. (2005) Dopant radiative cooling effects in indirect-drive Ar-doped capsule implosion experiments. Phys Rev E Stat Nonlin Soft Matter Phys 72.
- Patents and the Fourth Industrial Revolution (2017) The inventions behind digital transformation. European Patent Office in cooperation with Handelsblatt Research Institute.
- Agnès Grossel (2007) Spectrométrie Infrarouge et Détection de Gaz à L'aide de Lasers à Cascade Quantique. Thèse de l'Université de Reims Champagne-Ardenne. Spécialité: Physique.
- (2018) Analysis of fundamental electronic properties of nitride-based heterostructures and light emitting devices/diodes (LED's). Tyndall National Research Institute.
- https://www.laserfocusworld.com/articles/.
- http://nlte.nist.gov/NLTE10/.
- Loisel GP, Bailey JE, Liedahl DA, Fontes CJ, Kallman TR, et al. (2017) Benchmark experiment for photoionized plasma emission from accretion-powered x-ray sources. Physical Review Letters 119: 075001.
- https://www.researchgate.net/profile/Aj_Benita.
- D Benredjem, W Jarraha, F Gilleron, JC Pain, S Ferri, et al. (2015) Opacity calculations. Ge and Si dopants in ICF. HEDP 16: 23-27.
- Kline JL, Glenzer SH, Olson RE, Suter LJ, Widmann K, et al. (2011) Observation of high soft x-ray drive in large-scale hohlraums at the national ignition facility. Phys Rev Lett 106: 085003.
- Marriann Silveira (2014) OSIsoft at Lawrence Livermore National Laboratory. OSIsoft Federal Workshop.
- SVG Menon (2000) A primer on high energy density system simulations and typical results. 05 / SVGM / High Energy Density System Simulations.
- https://lasers.llnl.gov/news/papers-presentations/2016.
- KA Brueckner (1977) Fast-electron production in laser-heated plasmas. NUCLEAR FUSION 17: 6.
- Robert J Harrach, Ray E Kidder (1981) Simple model of energy deposition by suprathermal electrons in laser-irradiated targets. Physical Review 23: 887.
- LR Veeser (1978) Exploratory laser driven shock wave studies. Phys Rev Letters.
- RP Drake, HF Robey, OA Hurricane, Y Zhang, BA Remington, et al. (2002) Experiments to produce hydrodynamically unstable, spherically diverging system of relevance to instabilities in Supernovae. The Astrophysical Journal 564: 896È908.
- R Paul Drake (2006) High energy density physics. fundamentals, inertial fusion and experimental astrophysics. Springer, Shock Wave and High Pressure Phenomena.
- U Zastrau, A Sengebusch, P Audebert, E Brambrink, RR Fäustlin, et al. (2011) High-resolution radial Kα spectra obtained from a multi-keV electron distribution in solid-density titanium foils generated by relativistic laser-matter interaction. High Energy Density Physics 7: 47-53.
- T Döppner, OL Landen, HJ Lee, P Neumayer, SP Regan, et al. (2009) Temperature measurement through detailed balance in x-ray Thomson scattering. High Energy Density Physics 5: 182-186.
- Roberto C Mancini (1983) Doctoral thesis thermodynamics and hydrodynamics of compressed matter.
- H Brysk, PM Campbell, P Hammerling (1975) Thermal conduction in laser fusion. Plasma Physics 17.
- JJ MacFarlane, IE Golovkin, PR Woodruff (2006) HELIOS-CR - A 1-D radiation magneto hydrodynamics code with inline atomic kinetics modeling. Journal of Quantitative Spectroscopy and Radiative Transfer 99: 381-397.
- JJ MacFarlane, GA Moses, RR Peterson (1995) BUCKY-1 A 1-D radiation hydrodynamics code for simulating inertial confinement fusion high energy density plasmas. UWFDM-984.
- JP Christiansen, DETF Ashby, KV Roberts (1974) MEDUSA a one-dimensional laser fusion code. Computer Physics Communications 7.
- Naofumi Ohnishi (2012) Toward an accurate numerical simulation of radiation hydrodynamics in laser ablation plasmas. High Energy Density Physics 8: 341-348.
- M Fatenejad, B Fryxell, J Wohlbier, E Myra, D Lamb, et al. (2013) Collaborative comparison of simulation codes for high-energy-density physics applications. High Energy Density Physics 9: 63-66.
- J Osterholz, F Brandl, M Cerchez, T Fischer, D Hemmers, et al. (2008) Extreme ultraviolet emission from dense plasmas generated with sub-10-fs laser pulses. AIP Physics of Plasmas 15.
- TWJ Dzelzainis, J Chalupsky, M Fajardo, R Faustlin, PA Heimann, et al. (2010) Plasma emission spectroscopy of solids irradiated by intense XUV pulses from a free electron laser. High Energy Density Physics 6: 109-112.
- A Mancic, J Robiche, P Antici, P Audebert, C Blancard, et al. (2010) Isochoric heating of solids by laser-accelerated protons: Experimental characterization and self-consistent hydrodynamic modeling. High Energy Density Physics 6: 21-28.
- EI Moses (2010) Advances in inertial confinement fusion at the National Ignition Facility (NIF). Fusion Engineering and Design 85: 983-986.
- AGR Thomas, M Tzoufras, APL Robinson, RJ Kingham, CP Ridgers, et al. (2012) A review of Vlasov-Fokker-Planck numerical modeling of inertial confinement fusion plasma. Journal of Computational Physics 231: 1051-1079.
- Paul A Keiter, Katie Mussack, Sallee R Kleina (2013) An experimental concept to measure opacities under solar-relevant conditions. High Energy Density Physics 9: 319-324.
- TS Perry, RF Heeter, YP Opachich, PW Ross, JL Kline, et al. (2017) Replicating the Z iron opacity experiments on the NIF. High Energy Density Physics 23: 223-227.
- AJ Benita (2018) Calculation of temporal plasmas of XFEL experiments with a relativistic collisional radiative average atom code. Physical Science International Journal.
- AJ Benita (2018) Comparison of iron plasma atomic and radiative properties computed with a relativistic collisional radiative average atom code versus other models. Asian Journal of Research and Reviews in Physics.
Author Details
AJ Benita1,2*
1Plasma Atomic Physics Group, Madrid Polytechnic University, Spain
2Physics Department, Las Palmas Canary Islands University, Spain
Corresponding author
AJ Benita, Plasma Atomic Physics Group, Madrid Polytechnic University, 28006 Madrid, Spain; Physics Department, Las Palmas Canary Islands University, 35017 Las Palmas de Gran Canaria, Spain.
Accepted: August 30, 2018 | Published Online: September 01, 2018
Citation: Benita AJ (2018) Calculation of Silicon Plasmas with a Relativistic Collisional Radiative Average Atom Code. Int J At Nucl Phys 3:009.
Copyright: © 2018 Benita AJ. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper, it is illustrated the computational capability of the collisional radiative model ATMED CR for calculating accurate relativistic populations including nlj-splitting, mean charge, atomic and radiative properties and processes rates of photoionized silicon plasmas for astrophysics and inertial confinement fusion sciences. Experiments in Sandia's Z-machine with Accretion-Powered X-Ray Sources have been carried out in a regime comparable to astrophysical plasmas, where radiative processes are more dominant than collisional ones for setting the plasma ionization and relativistic population distribution. It will be checked the importance in calculations of radiative rates as stimulated emission, photoionization and photorecombination, considering the influence of an optical thickness as well of the plasma through the photon confinement probability formalism. Besides, silicon is a chemical element of the greatest importance for nanotechnology, electronics, astrophysics, inertial confinement fusion, so in turn the study of its atomic structure as well as the collisional and radiative processes rates in solid state, as warm dense matter or as a plasma component, is indispensable.
Keywords
Screened hydrogenic atomic model, Collisional radiative average atom code, Photoionized plasmas of silicon, Combination of planckian radiation fields
Introduction
The collisional radiative code ATMED CR [1-5] developed in the Average Atom formalism has been conceived to compute the population distribution of relativistic atomic levels (nlj-splitting), the average ionization as well as the main atomic and radiative properties of steady-state and temporal plasmas of pure chemical elements or mixtures. The atomic model inside ATMED CR is based on a New Relativistic Screened Hydrogenic Model (NRSHM) with a set of universal screening constants including nlj-splitting that has been obtained by fitting to a large database of 61,350 atomic high-quality data entries, compiled from the National Institute of Standards and Technology (NIST) database of U.S. Department of Commerce and from the Flexible Atomic Code (FAC) [6,7]. The calculation of accurate relativistic atomic populations including nlj-splitting of electronic orbitals, improves the precision of atomic properties as mean charge, rates and the resolution of spectral properties as opacities and radiative power losses, with respect to collisional radiative average atom codes as XSN of W. Lokke and W. Grasberger of 1977 with n-splitting [8] or with nl-splitting [9-11]. ATMED CR has become a reliable benchmark tool for studying and modeling well characterized theoretical and laboratory photoionized plasmas, with emphasis on their atomic kinetics and radiative properties. These plasmas type constitute a science opportunity in the fields of inertial fusion science, high-energy-density physics and their applications, combining experimental and theory effort for developing and improving current collisional radiative codes [12-16]. In laboratories, progression of increasing ionization parameter ξ (erg.cm/s) in photoionized plasma experiments is impressive and relevant for astrophysical and nuclear fusion applications. There are experimental platforms at Z-Pinch machines currently working on photoionized plasmas in several configurations, changing the X-ray flux at targets like a gas cell or an expanding foil. Silicon is also a fundamental material for nanotechnology and semiconductors, so as a consequence the study of its atomic structure is mandatory nowadays. It is fundamental for microelectronics and optoelectronics the development of lasers with quantum dots, lasers of diodes, lasers of quantum cascades, III-V photonic devices as InP-based lasers and modulators for their integration with silicon photonics for circuitry consisting of SiC light emitting devices/diodes (LED's) or GaN-on-Si power architectures, etc. [17-20].
The paper is organized as follows. In Sections 2 and 3 there are modeled with ATMED CR silicon steady state and temporal plasmas, some of them proposed in the 10th Non-LTE Code Comparison Workshop [21], of interest for several fields of research in high energy density physics as Z-Pinch machines or astrophysics, inertial confinement fusion, as well as for silicon photonics and atomic characterization. All plasma cases correspond to real associated experiments carried out in laboratories, giving to the code ATMED CR a realistic usage and a practical dimension, at least in order to compute statistical averaged plasma properties through a very complete and equilibrated collisional radiative balance of an average atom. Section 4 contains main conclusions.
Modeling of Photoionized Plasmas
Resolution of average atom equations with planckian radiation fields
Considering the rates that populate and depopulate the average atom relativistic orbitals, the system of equations can be written this way:
This rates equation system is mathematically coupled with the spatial and temporal (r,t) radiation transport equation:
Being
• I(r,t,v,e): Radiation specific intensity at the photon frequency v and propagation direction along e vector.
• & j(r,t,v): Radiation absorption and emission coefficients.
With the objective of speeding up calculations, the equations are considered as decoupled in a lot of collisional radiative models, because of representing the radiation fields by diluted or with full intensity Planckian photon energy distributions. Once the CR balance has been resolved and the relativistic orbital populations have been computed, the radiative properties are calculated also with a UTA or MUTA line profile much more complete and refined including Doppler, Natural, Stark and Dielectronic broadenings. If the plasma is thick, it is also considered a semi-infinite foil of thickness L equivalent to plasma radius, supposing that the average ion representative of the whole plasma is located at the half of the foil (d = L/2) [9-11]. The probability of a photon escaping from the half of the foil in whatever direction is defined as follows with the first exponential integral E1:
Being then the optical thickness of the foil in terms of opacity (cm2/g), density (g/cm3) and plasma length (cm):
It is used the photon confinement probability applied to radiative rates defined as:
To simplify calculations, it is supposed that radiation emissions from the plasma itself are transparent, so the radiation emitted from the plasma escapes considering negligible its reabsorption in line profiles for bound-bound or bound-free transitions. This way, if this source is several orders of magnitude greater than the radiation source emitted by the plasma, only the radiation coming from the Planckian source can be reabsorbed and generate processes of photoexcitation, photoionization and their inverse ones by detailed balance. depends on the plasma absorption coefficients which in turn depend on the average atom populations in whose calculation the radiative rates take part, being these rates a function also of the photon energy distribution . It is simulated the optical thickness of the plasma through a photon distribution which corresponds to the Planckian function multiplied by the photon confinement probability :
The description of main parameters in formulas of the average atom of the whole plasma is:
• : Photon Confinement probability factor for Planckian Radiation Field number N.
• : Electronic temperature.
• : Radiation temperature of Planckian Radiation Field number N.
• : Dilution factor of Planckian Radiation Field number N.
• : Inverse of brightness temperature Tv.
• : Excitation energy between relativistic orbitals i and j.
• : Electronic chemical potential.
• : Reduced electronic chemical potential.
The rate of photoionization for an electron of energy level i, going to the continuum is as follows:
The rate of photorecombination (radiative recombination) to energy level i, is calculated assuming local thermodynamic equilibrium LTE through detailed balance with the photoionization:
The photoabsorption/photoexcitation cross section associated to an electron being promoted from an energy level i to an upper level j is provided by:
Where is the spectral line function profile approximated by a Dirac's Delta. The photoabsorption rate considering the photon confinement probability then results:
The rate of photoemission (stimulated + spontaneous) from level j to a lower level i is provided by:
In optically thick plasmas, the formalism of photon confinement probability is a very convenient tool, so that simply applying it to radiative rates as in the previous formulas it is obtained a solution which is practically independent of the exact plasma shape.
For selecting the energies or frequencies at which the photo processes occur in a bound-bound line profile as Figure 1, it is included in ATMED CR an algorithm which is equivalent to look for the energy of an electronic transition by photoexcitation between two relativistic energy levels in the photon energy grid of 14,900 nodes.
This energy must be within the values in eV of two consecutive nodes for a grid at the radiation temperature of the plasma.
It is also allowed some photo absorption in the wings at frequencies at around the line central frequency corresponding to an electronic transition, because the grid is very thin and great difference doesn't exist in energies between two consecutive nodes. This way a process of photoexcitation for an electron is introduced at the selected photon energy. At all the selected energies the photon confinement probability factors are updated inside each iteration and an iterative loop is used considering the plasma characteristic dimension L (cm). The detailed explanation of operating schemes of the code can be found in Reference [2]. Finally, once the populations have been computed in ATMED CR having supposed the spectral line function profile approximated by a Dirac's Delta for getting simpler formulas, the radiative properties are calculated with a more complete and refined Voigt line profile which includes the Doppler, Natural, Stark and Dielectronic broadenings as it was a fore mentioned. As well it is used a bound-bound absorption cross section that gathers lines, being equivalent to apply the Unresolved Transition Array (UTA) formalism; or another cross section that provides a discrete spectrum of individual lines (MUTA) between the average atom relativistic orbitals. An incident radiation field can also be reproduced through combining k Planckian distributions, each one of them multiplied by its dilution factor and by its photon confinement probability. So, in turn the photo absorption rate considered inside ATMED CR is as follows:
In Workshop NLTE-10 [21] for a steady state plasma of silicon, there are considered three (k = 3) incident Planckian distributions [48 (0.28) + 92 (0.081) + 170 (0.0067)].
The rate of photoemission (stimulated + spontaneous) from level j to a lower level i is provided by:
The rate of photoionization from level i to the continuum is provided by considering the contributions of three Planckian distributions for all incident photon energies hv (eV) at each radiation temperature:
Considering as the inverse of brightness temperature the next formula depending on radiation temperature and dilution factor:
The rate of photorecombination (radiative recombination) to energy level i is calculated assuming local thermodynamic equilibrium LTE through detailed balance with the photoionization:
Although the expression has been deduced from the hypothesis of local thermodynamic equilibrium (Te = Trad), this formula depends only on atomic magnitudes and on electronic temperature Te.
Application of Resolution of Average Atom Photoionized Plasmas in Atmed Cr
Sandia's Z-machine experiments
General description
For adjusting complex spectra of satellites as Chandra, Vela X-1, Cygnus X-3 or XMM, it is necessary to consider not only one Planckian radiation field, but an appropriate combination of several fields, characterized each one of them by its radiation temperature TR eV and dilution factor in laboratory experiments. Precise collisional radiative models are needed with a useful treatment of atomic processes rates, especially of photorecombination/photoionization conditioning mean charge and spectra, for determining for example, conditions found in systems of photoionized accretion-powered plasma in accretion disk observed in outer space. Cygnus X-1 belongs to a high-mass X-ray binary system about 6000 light years from the Sun that includes a blue supergiant variable star designated HDE 226868. Experiments are performed for computing plasma like the aforementioned one (Figure 2). The main parameters for calculations of Si photoionized plasmas with several optical thicknesses or radius provided by Workshop NLTE-10 [21] are detailed in Table 1.
The measured irradiance in laboratory is above ~167 eV photon energy capable of ionizing silicon in the experiments finding an ionization parameter ξ~20 erg. cm. s-1 [22]. These experiments have been carried out using an X-ray source driven by 26 MA peak current from Sandia's Z machine which generates a 1.6 MJ X-ray burst with a 3 ns full-width-half-maximum (FWHM) and 220 TW peak power, creating a photoionized silicon (Z = 14) plasma, with a unique Planckian radiation field or with a combination of three, each one characterized by the radiation temperature and dilution factor.
Considering the characteristics of real experiments in laboratory, the calculations of mean charge are very accurate with respect also to the detailed codes XSTAR and ATOMIC, because the collisional radiative balance of ATMED CR is a very complete statistical average of the results of detailed models, even for a combination of three Planckian radiation fields. The resolution provides information about the order of magnitude of processes rates, atomic and radiative properties characterizing the specific plasma conditions, with high sensitivity also to plasma radius.
Photoionized thick plasmas of silicon with 1 or 3 planckian radiation fields
As a direct consequence of the relativistic splitting of matter structure of ATMED CR code and the high sensitivity to slight changes in the experiment characteristics (plasma radius R, Ne, Te, TR, etc.), it can be accurately observed in Table 2, the influence of thermodynamic variables on mean charge, as well as of computing collisional-dominated plasmas not being photoionized [22,23] for which the dominant charge state is Si+5 (F-like). According to ATMED CR at Ne = 1E + 19 cm-3, Te = 33 eV, TR = 0 eV and R = 0 cm, mean charge is Zbar = 3.64; and at Ne = 1E + 19 cm-3, Te = 30 eV, TR = 0 eV and R = 1.2 cm, mean charge is Zbar = 3.62, so the dominant charge states for non-photoionized plasmas driven by collisional processes are in the range of Si+5 (F-like) and Si+3 (Na-like). As it is mentioned in the article of the real experiment [22], if the input parameters are adjusted to favor more recombination with higher rates values for this atomic process, the mean charge is at around Zbar~10. This statement is corroborated also by calculations with ATMED CR code especially for the plasma case of three Planckian radiation fields at Ne = 3E + 19 cm-3 and plasma radius R = 1.2 cm, for which including or not the photoionization and photorecombination rates in the CR balance solution provides respectively mean charges of Zbar = 10.186 or Zbar = 11.75 (Table 2).
Although for other plasma conditions, there is little difference, it is better to compute including photorecombination rates also for inner orbitals in order to have very exact values of mean charge and other plasma properties. It can be noticed also in Table 2 the great importance of applying photon confinement probability to the stimulated emission radiative rates, although the computation time is greater. Considering only spontaneous emission as radiative decay processes for lowering the duration of calculation, makes the code insensitive to plasma length or radius (cm). When including stimulated emission with photon confinement probability, check especially the plasma cases of three Planckian radiation fields at Ne = 3E + 19 cm-3 and plasma radius R = 0.3 or 1.2 cm for which the code calculates mean charges of Zbar = 11.54 or Zbar = 10.186; while not including stimulated emission and considering only spontaneous emission provides for R = 0.3 cm a value of Zbar = 10.17, turning the code into an insensitive tool to plasmas optical thickness for these calculations in so narrow a range of thermodynamic conditions.
It is as well highlighted the good performance of the code ATMED CR for the combination of Planckian fields with respect to the results of mean charge calculated with XSTAR and ATOMIC, within the range Zbar = 9.9 ÷ 10.3 for Ne = 1.7E + 19 cm-3 and Zbar = 11.2 ÷ 11.4 for Ne = 3.4E + 19 cm-3 according to Figure 3 of Reference [22]. Some test cases have been carried out to demonstrate the high sensitivity of ATMED CR to combination of several Planckian fields for plasmas of pure elements with low atomic number as it is illustrated in Table 3. For example, for silicon, the radiation fields 48 eV (0.28) or 170 eV (0.0067) acting in a separated way produce a mean charge of Zbar = 3.68 & 3.64 respectively, but both combined produce a mean charge of Zbar = 11.31.
Other plasmas have been tested which highlight also the sensitivity of ATMED CR code to combination of several Planckian fields for pure elements with intermediate atomic number as iron, high atomic number as gold or even for mixtures as Fe + NaF as it is displayed in Reference [23] and Table 3. The accurate data displayed in tables are a direct consequence of ATMED CR code being capable of computing fine grids of collisional radiative calculation for a great quantity of points inside a range not too much wide, see section 6.8 of thesis book [2]. The code is robust and sensitive to very small jumps of 2 eV in Te and of 0.25 cm-3 in Ne or even smaller, without producing the typical problems that sometimes appear in the operation of a FORTRAN code (NaN, + Infinity, etc.). This degree of resolution in the thermodynamic variables is due to the relativistic splitting of the atomic structure and can be appreciated in the evolution of plasma parameters calculated for example in the experiments of silicon with Sandia's Z machine. With slight jumps in electronic temperature, electronic density and plasma radius ATMED CR is very exact computing without FORTRAN errors.
Computed Radiative Power Losses (RPL) and Rosseland (KR) and Planck (KP) mean opacities with Unresolved Transition Array (UTA) or Mixed Unresolved Transition Array (MUTA) formalisms are illustrated in Figure 3. The resolution of frequency resolved radiative properties as opacity and as Rosseland and Planck mean opacities values is also accurate as a consequence of considering a very fine grid of photon energies for a specific density-temperature point. The grid of ATMED is equal to the one of ATOMIC code, including 14,900 temperature-scaled photon energies being chosen to encompass a large photon energy range, and to provide a sufficient density of points in the region where the Rosseland weighting function is peaked.
ATMED CR performs calculations of rates, including photon confinement probability factors per electronic transition for photoexcitation and photo deexcitation rates or PC factors per photon frequency node in the grid for photoionization and photorecombination rates.
More rates for silicon of astrophysical plasmas are collected in Reference [2]. When in calculations the oscillator strength for a given electronic transition between two orbitals is zero, this means that the probability of taking place a process of photoexcitation or photo deexcitation is null and in turn the rate figure is also zero. According to Ref. [22] in the photoionized plasmas by contrast with the collision-dominated silicon plasmas, photoionization is as much as important as collisional ionization, being both atomic processes comparable in the balance. Furthermore, radiative and dielectronic recombination are comparable to or greater than three-body recombination for the conditions considered here [21]. In Table 4 it is displayed the difference of some total rates depending on the plasma case computed with ATMED CR, and the same conclusions aforementioned [22], can be extracted observing the order of magnitude for atomic processes rates calculated in the statistical approach of the average atom formalism. Although for the sum of all orbitals photoionization results lower than collisional ionization for some plasma cases, for some relativistic orbitals photoionization figure results higher than collisional ionization one. For thick plasmas at TR = 0 eV computed with ATMED CR, it is used the formalism of applying an escape factor to each bound-bound electronic transition in the spontaneous emission rate because there is not stimulated emission.
Capsules for Inertial Confinement Fusion (ICF)
Numerous mixtures have been analyzed susceptible of being candidate materials for the ablator of capsules in indirect ICF in NIF (National Ignition Facility). The optimal value of Rosseland mean opacity KR is not always the maximum reachable with the greatest percentage of dopant according to the specifications for the capsule roughness, but instead KR should be that value which provides the maximum efficiency with the lower number of hydrodynamic instabilities in order to finally reach ignition. Mixtures of silicon have been studied for their use as ablator or as a signature layer in the capsule, see Figures 4 and Figure 5. These mixtures can be used in solid state or under the shape of foams or aerogels, for the typical conditions of indirect ICF within the density range 10-3 ÷ 10 g/cm3 and the temperature range 10 ÷ 360 eV.
Steady state plasmas
In Reference [2] there are illustrated properties of SiO2 and SiC (5%C) plasmas in LTE or NLTE regimes in stationary state and considering a Planckian radiation field incident over the capsule at 300 eV, typical value registered by Dante inside cylinder hohlraum. More data for silicon and SiO2 in conditions common to ICF can be found in Ref. [14,15]. There are also mixtures compared with opacity profiles calculated by Pim Pam Pum (PPP) code [24].
Time dependent plasmas of mixtures
Experiments employing gold vacuum hohlraums heated with laser energies in the range between 150 ÷ 635 kJ and reaching radiation temperatures of up to 340 eV have been carried out, showing high X-ray conversion efficiencies of 85% ÷ 90% at NIF, USA [25]. In Figure 6 there are displayed graphs belonging to these real experiments showing a brief description:
All data and signals from SCADA's, sensors, R/O controllers, power meters, etc. constitute a design of High Performance Computing (HPC) arquitecture at LLNL, accelerating data center efficiency also with the OSIsoft PI System™ which gathers data measurements from experiments which are nowadays much more reliable than ever before [26]. At around 300 TW of laser peak power the radiation temperature inside the hohlraum can surpass 300 eV but at 25 TW, TR over capsule can't exceed 250 eV [27]. There are considered temporal profiles which are a consequence of radiation and electronic temperatures evolutions as seen by hohlraum and capsule proportional to X-Rays from a laser peak power illumination of 25 TW (TJ/s) incident on the hohlraum walls, providing the radiation temperature on capsules as Nova Hohlraum data facility [27] or as OMEGA data facility (Figures 7 and Figure 8). Hohlraum walls radiation temperature is 11 ÷ 13 eV greater than the radiation temperature over the capsule surface corresponding to an increase of 6 ÷ 7% in temperature and 25 ÷ 30 in radiation flux in Hohlraum walls.
As a practical example of computing with ATMED CR including nlj-splitting of matter structure statistical averaged properties of realistic plasmas in experiments, as equal as they are calculated by XSN atomic physics code with n-splitting, there are considered in Figures 7 and Figure 8 capsules of densities in (g/cm3) CH (1.047), CH + 2% Si (1.101), CH + 0.8% Br (1.0) that are manufactured using a glow-discharge polymer process having a composition of 57.2% hydrogen. It is considered as constant in time the density, supposing null or negligible losses of mass through laser entrance holes or patches for diagnostics located inside the hohlraum. The computation time without photoionization and photorecombination rates in the CR balance is at around 4 minutes while including these processes gives way to CPU times of 1 hour or more for the same capsule and the same temporal profiles of Te (t), TR (t). Calculations have been performed considering a radiation temperature over the ICF capsule and central heating achieved by X-rays radiation, as drive onto capsule by VISRAD. The electronic temperature as seen by the capsule is supposed to be also coincident with the radiation temperature over the capsule surface. The mixture mean charge does not practically vary in time due to the small fraction of partially ionized silicon or bromine and the low atomic number of the main components carbon and hydrogen, which in these conditions are highly ionized. Nevertheless, significant variations in the Rosseland and Planck mean opacities, in frequency resolved opacity and in the radiative power losses are produced. In Reference [2], it is explained how to couple ATMED CR program with a hydrodynamic code through a flow diagram for simulating targets irradiated by laser beams in direct drive scheme using a thermal flux limiter factor (FLFT), see also next Section 3.
In a similar way radiation-hydrodynamic codes of hohlraums on the NIF are coupled with the XSN atomic physics model also with a flux limiter (FLFT = 0.05) for thermal heat transport as in Figure 6. In this range of thermodynamic conditions, ATMED CR computes perfectly plasma properties. More data of temporal plasmas of hohlraum walls or capsules are collected in References [1,2], considering that average temperatures equivalent to matter/electronic temperature near the hohlraum center are higher than radiation temperature as seen by the capsule. Basically, inside each time step the hydrodynamic code searches for and interpolates in tables calculated with ATMED CR the chemical potential and plasma mean charge Zbar for computing electronic and ionic thermal conductivities and relaxation time ion-electron as a function of temperatures and matter density. And then this data act as input parameters in the resolution of the code Lagrangian equations of conservation of mass, momentum and energy of the plasma system of ions and electrons created by the laser-matter interaction. For each spatial and temporal node of conditions given by temperature, density and atomic number of a pure element or of a mixture (Te - TR - ρ - Z - ZMixture), the hydrodynamic code uses the data for solving also ions and electrons equations of state calculating the electronic pressure, internal energy and specific heat, see also next section 3.
As it is displayed in Figure 7, the flux and radiation temperature reached result from modulating the laser beam energy (kJ) incident over the hohlraum walls as from 25 TW laser peak in Nova [27].
As it is displayed in Figure 8, the flux and radiation temperature reached result from modulating laser beam energy (kJ) incident over the hohlraum walls as OMEGA data facility.
Modeling of Plasmas Created from Irradiated Matter
Resolution of average atom equations in ATMED CR coupled to HYAT Code
The code HYAT is used to simulate irradiated targets by laser light through the numerical resolution of the fluid equations [28]. Its hydrodynamic model consists of two subsystems, electrons and ions. It is considered a fluid element which contains a great number of particles as the Avogadro's number and the inertia of each fluid element is determined by the quantity of ions inside it, because the mass of electrons is negligible with respect to the mass of ions. Coupled and connected to ATMED CR with partial ionization [2], the average atomic number of the material Z is replaced by the local mean charge Zbar in all formulas of Lagrangian equations of mass conservation, momentum conservation and specific heat of ions and electrons inside the plasma. The numerical method as well as the spatial and temporal discretization of the irradiated target and plasma physical system, is carried out dividing the main characteristic dimension of the target in several zones or cells for the calculation of thermodynamic variables. The last cell on the right side of the target is the one belonging to laser beam incidence. The operating scheme and the flow diagram of the hydrodynamic code HYAT connected to the collisional radiative model ATMED CR is displayed in Ref. [2]. Some of the main theoretical formalisms used in the code HYAT are described in the references [29-31]. In the last decades, numerous experiments of irradiated targets by laser beams have been carried out [32-35]. With the resultant hydrocode HYAT 1D + ATMED CR several examples of simulations in one dimension (1D) of plane and cylindrical targets have been performed.
The total energy of laser light ET absorbed by the irradiated target, corresponding to a laser pulse PL(t) of incident power represented by a Gaussian trimmed temporal profile with dispersion or pulse width σ, pulse duration τ, time t0 for peak of maximum power P0, is as follows:
The electromagnetic radiation of laser pulse which penetrates from outside transfers gradually its energy to electrons of plasma by the inverse bremstrahlung mechanism [29,30], producing an exponential attenuation with distance r of incident energy so that the power inside the plasma is:
: Attenuation coefficient by inverse bremsstrahlung. R0: Interface plasma-vacuum.
Application of HYAT 1D + ATMED CR hydrocode to irradiated silicon nanowires
Silicon is the most prevalent material in electronics for mobile phones, displays, screens or computers. Physicists are using also nanotechnology to produce nanowires which help increase the efficiency of solar energy cells by concentrating light particles on p-n junction silicon solar cells. Nowadays, a myriad of silicon transistors is responsible to transmit the information on a microchip. The transistors can be arranged lying flat next to each other in a planar array, but further miniaturization of transistors with a planar structure while reducing the cost of electronics, although being desirable is difficult to achieve due to fundamental physical limits. Currently, researchers are developing nanometer-sized wires made of silicon which have a large potential for new chip architecture, overcoming the physical limits of downscaling and integration of microchips. This requires a detailed investigation and understanding of their electronic properties which is technologically challenging due to the ultra-small size of the nanowires. One new approach is to fabricate transistor architecture in three-dimensions, turning the silicon transistors by 90 degrees so that they stick out of the chip substrate like tiny columns, instead of arranging them flat on the substrate (Figure 9). Besides, numerous vertical transistors could be located on the same area occupied by only one planar transistor. This would finally be the step to develop a new generation of transistors, through the manufacturing of vertical silicon nanowire arrays with well-known electrical properties (http://www.nanotech-now.com/).
So silicon is a fundamental material for nanotechnology, semiconductors, microelectronics and optoelectronics and the investigation of its atomic structure and processes is indispensable through experiments as that performed in laboratories for analysis of the interaction of a femtosecond laser pulse of relativistic intensity with an array of aligned nanowires creating ultrahigh-energy density (UHED) plasma [20].
In the irradiation process, electrons are ripped from the surface of the nanowires by the intense laser field that accelerates them into the gaps between the wires to acquire high energy. Electron collisions with the nanowires heat the material to extreme temperatures, causing the nanowires to explode creating the plasma. This ultrahigh-energy density regime is characterized by pressures greater than a gigabar and can be found in the center of stars and in the spherical compression of inertial confinement fusion (ICF) capsules driven by lasers. The UHED plasma regime is of interest for fusion studies and for the study of atomic processes in the conditions encountered in extreme laboratory and astrophysical environments.
Collisional radiative codes are indispensable also to characterize the plasmas created in UHED regime and from exploding vertical wires, for creating thin grids of parameters as mean charge, chemical potential, atomic processes rates, mean opacities, etc. In turn, these plasma parameters are used as an input for hydrodynamic simulations of irradiated matter, computing this way evolution profiles versus time of density with respect to the ordinary one of silicon in solid state ρ = 2330 kg/m3, electronic and ionic temperatures with respect to the initial ones of ambient temperature 300 K (1 eV = 11604.525 K → 2.58539E-02 eV = 300 K), shockwaves propagation, etc.
With ATMED CR code, fine grids of the aforementioned parameters of silicon plasmas have been calculated and used along with the hydrodynamic code HYAT [36] for simulating irradiated vertical high not flat nanowires of silicon (Figure 9), in planar geometry considering as their characteristic dimension the longitudinal height. This way, the simulations correspond to the main data of Table 5a, considering P0 as the maximum peak of laser pulse and FLFT as the thermal flux limiter factor.
Temporal evolution of density, electronic and ionic temperatures are shown on Table 5b for some representative instants of the calculation. The evolution of variables of one irradiated vertical high not flat nanowire of silicon of 25 μm is illustrated in Figure 10, not being observed big changes in density along its length.
Simulations of irradiated silicon nanowires with dopants could also be managed considering a mixture of elements for the plasma parameters calculation. For example, ultrahigh-vacuum transmission electron microscopy, Rutherford backscattering, laser irradiation (Figure 10) have been applied to elucidate the interaction mechanisms of pure titanium or titanium disilicide nanowires (TiSi2 NWs) on Si (111) or Si (110) substrate.
As an illustrative example, with the code HYAT + ATMED CR based on partial ionization, the irradiation of a titanium (Z = 22) target sheet of 2 μm has been analyzed at initial density 4.507 g/cm3, adjusting the laser pulse in order to reach electronic temperatures of 24 ÷ 46 eV. HYAT + ATMED CR code calculates the data of Table 6a, Table 6b, Table 6c and Table 6d in high agreement with the values displayed on Figure 11 obtained with HELIOS 1D code [34].
So, the order of magnitude for reached densities versus time is good, it is produced a heat wave propagation outward the target and the penetration of the shockwave inside the target of Ti is also in accordance with HELIOS, see Figure 12 and Table 6a for P0 = 2000. So, the results for silicon as pure element can be also trusted. With HYAT 1D + ATMED CR, the reached density versus time for several values of P0 as the maximum peak of laser pulse in the range 1000 ÷ 9000 is as follows in Table 6b, and for P0 = 9000 variables evolution is as indicated in Table 6c.
With P0 = 2000 the evolution of density profile is more parabolic and by contrast with P0 = 9000 the evolution of density is a more peaked profile with greater shockwave penetration length and greater peak density for all instants. The peaks of density due to shockwaves inside the analyzed targets computing with HYAT supposing total ionization or with HYAT 1D + ATMED CR considering partial ionization, are very similar in the case of silicon, but for titanium the differences are considerable replacing the atomic number Z by plasma mean charge Zbar, and also the penetration length inside the material is greater (Table 6d). With HYAT, the reached density versus time is too excessive, so the use of partial ionization becomes mandatory for elements of intermediate atomic number as titanium (Z = 22).
Similar experiments with irradiated sheets of beryllium foils of 250 μm have been carried out reaching electronic temperatures of 18 eV and mean charges around Zbar = 2.3, achieving isochoric heating, in agreement with simulations performed by the hydrodynamic one-dimensional code HELIOS, considering the laser parameters corresponding to the real experiment [35]. With code HYAT + ATMED CR based on partial ionization, the irradiation of the beryllium target sheet of 250 μm has been analyzed, adjusting the laser pulse in order to reach electronic temperatures of 18 eV. HYAT + ATMED CR calculates mean charges in the grid at around Zbar = 2.39. Peak densities are at 0.5 ns at around 5.2 g/cm3 with HELIOS and 2.5 g/cm3 with HYAT + ATMED CR and at 1.4 ns, at around 5.2 g/cm3 and 2.099 g/cm3 respectively. With HYAT+ ATMED CR at 4.4 ns the peak density is 2.1 g/cm3, so the order of magnitude versus time is good. With HYAT and total ionization, the reached density at 1.4 ns is 6.3 g/cm3, but at 4.4 ns is 71.6 g/cm3, too excessive, so the use of partial ionization becomes mandatory also even for elements of low atomic number as beryllium (Z = 4).
The evolution with time of density of irradiated flat targets of 250 μm of beryllium with HELIOS is illustrated in Figure 13, not being observed big changes in density along its length. For other evolutions of thermodynamic variables as shockwave propagation velocity or length of penetration inside the irradiated target, there can be more discrepancies, fact which can also be due to different formulas used for solving the lagrangian or eulerian equations inside the codes [37-41]. The correct values will be the experimental ones and collaborative comparison of simulation codes for high energy density applications is fundamental [42]. For example, if the code HYAT + ATMED CR uses for ionic conductivity one formula with mean charge to the fourth power in the denominator Zbar4, and the code HELIOS computes instead with other formula just simply with Zbar, then the electronic conductivity is much more important and the results for final characteristics of shockwaves as speed generated inside the material or penetration length are within not a very narrow range.
HYAT + ATMED CR must be used only with elements of low or intermediate atomic number, for which there is little need of considering the energy transport by radiation. So, in turn, although HYAT + ATMED CR does not consider the energy transport by radiation, it is much more important the plasma conductivity because the zones of radiation conversion and reemission after being the target irradiated, are replaced for the aforementioned elements by only one conductivity zone where the energy transport is dominated by the electronic conductivity and the X-Rays conversion is very small.
In the last decades, numerous experiments of irradiated targets by laser beams have been carried out. Several simulations of plane and cylindrical targets have been performed with ATMED CR code [2]. For some elements if a hydrodynamic code considers total ionization, it would provide very oscillating temporal and spatial evolutions of thermodynamic variables, so it is better to use partial ionization through mean charge of a plasma to compute a good order of magnitude of pressure, density, temperature, shockwave velocity and penetration distance, etc., as well as a more stable evolution with less oscillations in the simulated targets of these variables.
Apart from the difference in the order of magnitude of variables as pressure, density, temperature, shock wave velocity, etc., it has been observed in graphical simulations a more stable evolution with less number of oscillations with the program HYAT 1D + ATMED CR and of greater duration time (ps).
A lot of hydrodynamic simulations of plane and cylindrical targets of pure chemical elements and mixtures have been made with HYAT 1D + ATMED CR, using partial ionization of matter through plasma mean charge. The order of magnitude of density peaks as well as penetration length of shockwave is really good in comparison with calculations of other codes.
As illustrative examples, the evolutions of thermodynamic variables for targets of carbon in initial solid state ρ = 2267 kg/m3 with MULTI-fs + FLY code [43], of several microns thick of aluminium with HYADES code [44] and 0.5 or 10 μm with ESTHER code [45] are very similar. The density peaks normalized to the solid density are of the same order of magnitude as well as the shockwave penetration length inside the target, not being very profound. The heat wave propagation outside the target is also well reproduced. In laboratories the real penetrations depths obtained in warm dense matter of aluminium are of (40 ± 10) nm at electron temperature Te = (23 ± 7) eV (U. Zastrau. COST Meeting, Hirschegg 2008).
For some targets as it is observed in Figure 10 of silicon with HYAT 1D + ATMED CR code or in Figure 13 of carbon with MULTI-fs + FLY code in Ref. [43], for some cells inside the target there is ablated material so instead a peak of density in these cells, density is lower than the initial one belonging to solid density at ambient temperature ρ = 2.267 g/cm3, and a rarefaction wave is produced. Even with a laser peak intensity of 3 × 1016 W/cm2, the density slightly surpasses 3 g/cm3 at 0.118 ps or doesn't reach 3 g/cm3 at 0.01 ps [43].
Summary and Conclusions
In this paper, silicon steady state and temporal plasmas are modeled with ATMED CR, proposed in the scientific literature or in the 10th Non-LTE Code Comparison Workshop [21] of interest for high energy density facilities. The study and investigation of silicon atomic structure as well as the collisional and radiative processes rates within plasma state as a pure element or in mixtures is of the utmost importance. The results of ATMED CR for silicon plasma properties can be considered as very optimal, according to the thermodynamic conditions registered in computational or real experiments of plasmas created in Z-machines or laser irradiated matter facilities. The iterative loops with the average atom in ATMED CR of thick photoionized plasmas, with radiation trapping accounted for with the photon confinement probability (PC) formalism applied to radiative rates, lead to a very useful and sensitive method for calculating statistical averaged plasma properties for this type of experiments. This avoids some of the typical difficulties that appear with a matricial resolution in CR balances, as enormous matrices of detailed collisional radiative codes or intensive calculations with long duration times of PC factors for a very fine grid of photon frequencies up to 14,900 nodes or per relativistic bound-bound electronic transitions between energy levels of several ionic configurations and charge states. The calculations are relatively accurate because the collisional radiative balance of ATMED CR is a complete statistical average of the results of detailed models as XSTAR and ATOMIC [22], even for a combination of three or more Planckian radiation fields or with elements of high atomic number and mixtures. Great advances have been made in achieving Inertial Confinement Fusion [46,47], being now data from experiments more reliable and effectively collected or analysed than ever before [26]. Whichever the case, if ignition is finally not reached, all the theoretical and experimental effort carried out in investigation of laser irradiated matter, energetic balance and in the analysis of atomic level structure has a parallel and direct impact on several fields of research [48,49], for studies in related disciplines like physics, chemistry, life sciences, materials for nanotechnology, etc. So, simulating thermal processes in interaction zones, absorption, reflection, radiation transfer, heat transfer by conduction and convection, evaporation and emission of material with numerical modeling of laser interaction with matter is fundamental. The plasmas computed in this work belongs to real associated experiments of laboratories, giving to the code ATMED CR a realistic usage and a practical dimension, for using it as a collaborative software and for benchmarking results of other codes against the statistical averaged plasma properties [50,51].
Acknowledgements
Special mention in this work for all the authors of References [6-11,36], because of the developed atomic model, the formulas of rates adapted to the average atom formalism which operate extremely well, and the hydrodynamic model HYAT 1D which coupled with ATMED CR code provides qualitative and quantitative correct simulations of laser irradiated matter.

