
International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 3, Issue 1
Orginal Article
DOI: 10.35840/2631-5017/2508
Structure and Energy of the Δn = 14 Series Fullerenes
Alexander I Melker1* and Tatiana V Vorobyeva2
Table of Content
Figures
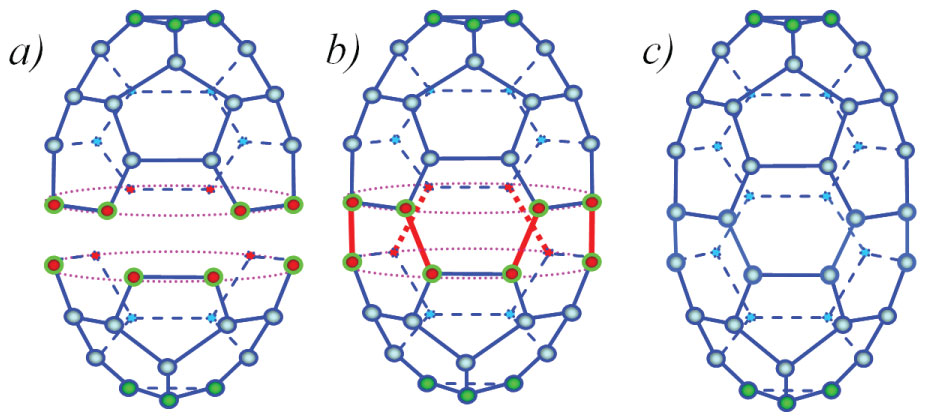
Figure 1: Joining two half-fullerenes C16 and C22 and fullerene C38...
Joining two half-fullerenes C16 and C22 and fullerene C38 obtained; a) Separate carbon cupolas; b) Intermediate compound; c) Penta12hexa9-polyhedron C38 after relaxation. Dark-red and light-blue balls are reacting and neutral atoms, respectively; light-blue solid and dashed lines are stable covalent bonds; heavy dark-red solid and dashed lines are new covalent bonds.
 Joining two half-fullerenes C18 and C24 and fullerene C42...
Joining two half-fullerenes C18 and C24 and fullerene C42...
Joining two half-fullerenes C18 and C24 and fullerene C42 obtained; notations are the same as before.
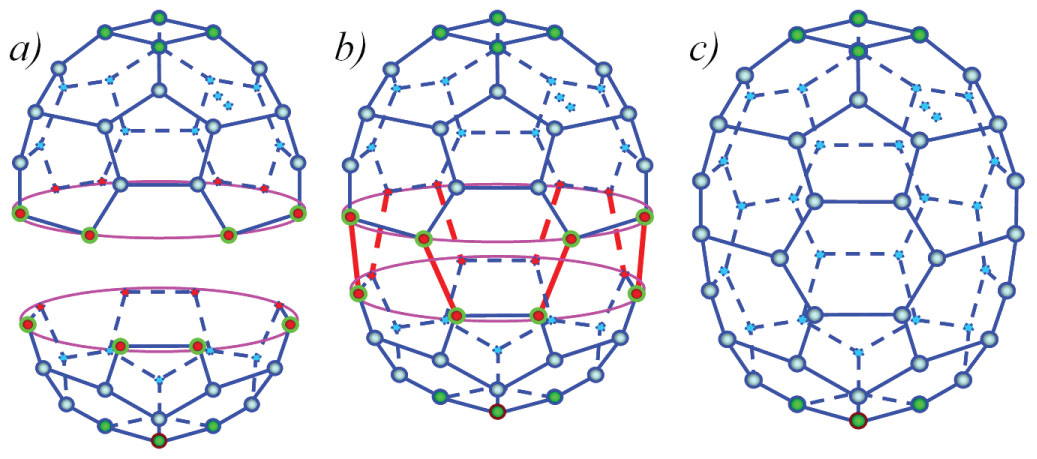
Figure 3: Joining two half-fullerenes C24 and C32...
Joining two half-fullerenes C24 and C32 and fullerene C48 obtained.

Figure 4: Joining two half-fullerenes C30 and C40 and fullerene C70 obtained.
Joining two half-fullerenes C30 and C40 and fullerene C70 obtained.
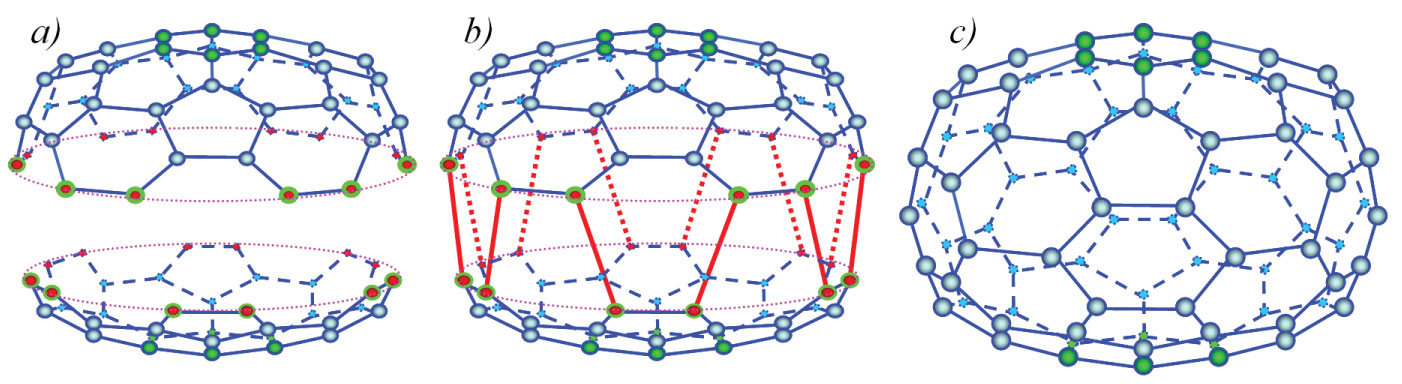
Figure 5: Joining of two half-fullerenes C36 and C48...
Joining of two half-fullerenes C36 and C48 and fullerene C84 obtained.
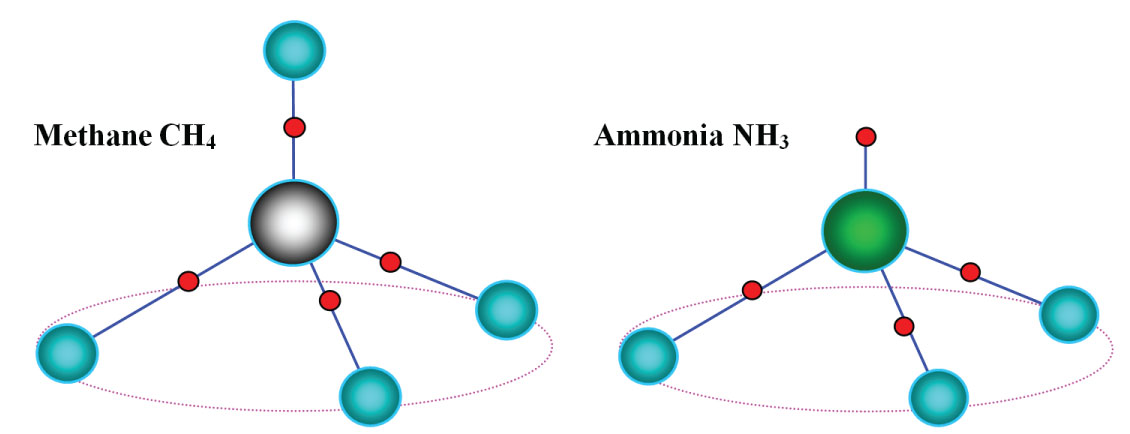
Figure 6: Structure of the Δn = 14 series fullerenes with...
Structure of the Δn = 14 series fullerenes with single and double bonds. Energy in kJ/mol.
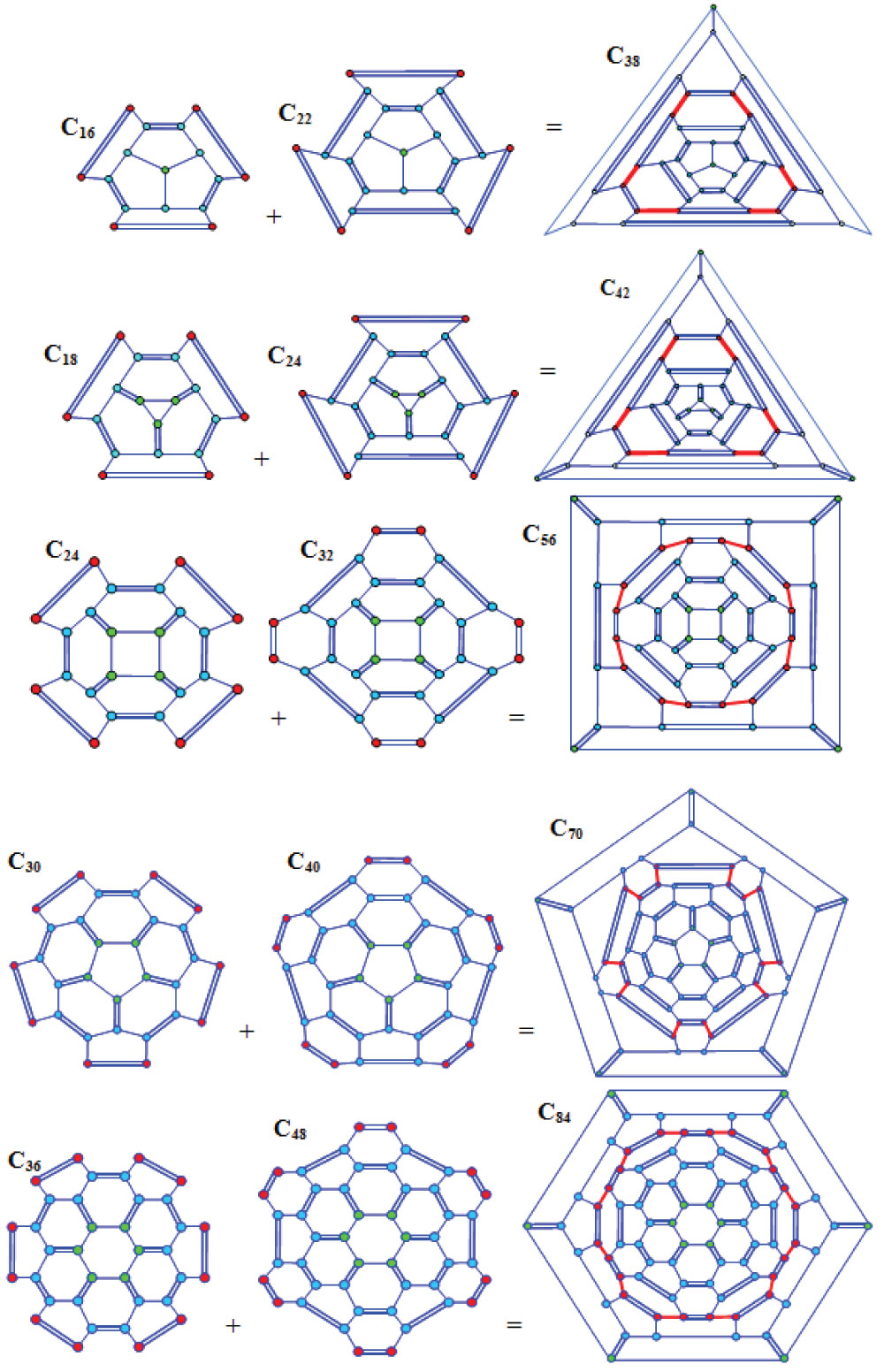
Figure 7: Fusion reactions of cupolas as connection of two graphs...
Fusion reactions of cupolas as connection of two graphs; all notations are the same as before.

Figure 8: RMethane and ammonia; red dots denote electron pairs.
Methane and ammonia; red dots denote electron pairs.
References
- AI Melker, MA Krupina (2017) Modeling growth of midi-fullerenes from C48 to C72. Materials Physics and Mechanics 34: 29-36.
- AI Melker, MA Krupina, RM Zarafutdinov (2017) Fullerenes of the Δn =12 series. Materials Physics and Mechanics 34: 46-50.
- AI Melker, TV Vorobyeva (2016) Fusion reactions of cupola half-fullerenes. St. Petersburg State Polytechnical University Journal: Physics & Mathematics 3: 209-216.
- MD Hanwell, DE Curtis, DC Lonie, T Vandermeersch, E Zurek, et al. (2012) Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. Journal of Cheminformatics 4: 17.
- AI Melker, Maria A Krupina, RM Zarafutdinov (2017) Fullerenes of the Δn = 10 series. Materials Physics and Mechanics 34: 37-45.
- P Schwerdtfeger, LN Wirz, J Avery (2015) The topology of fullerenes. WIREs Comput Mol Sci 5: 96-145.
- NV Sidgwick, HM Powell (1940) Bakerian lecture: Stereochemical types and valency groups. Proc Roy Soc Series A 176: 153-180.
- RJ Gillespie (1972) Molecular Geometry. Van Nostrand Reinhol Co. London.
- AI Melker, Maria Krupina (2006) Electronic theory of molecule vibrations. Proceeding of SPIE 1-15.
- AI Melker, MA Krupina (2010) Hidden symmetry or why cyclic molecules have so strange forms. Materials Physics and Mechanics 9: 11-19.
- AI Melker (1991) Modeling Experiment. Znanie, Moscow, 64.
- AI Melker, V Lonch (2012) Atomic and electronic structure of mini-fullerenes: From four to twenty. Materials Physics and Mechanics 13: 22-36.
- AI Melker (2014) Possible ways of forming mini-fullerenes and their graphs. Materials Physics and Mechanics 20: 1-11.
- AI Melker, SA Starovoitov, TV Vorobyeva (2014) Classification of mini-fullerenes on graph basis. Materials Physics and Mechanics 20: 12-17.
- (1988) Mathematical encyclopedic dictionary. Soviet Encyclopedia, Moscow, 848.
Author Details
Alexander I Melker1* and Tatiana V Vorobyeva2
1Department of Mechanics and Control Processes, Peter the Great St. Petersburg Polytechnic University, Russia
2Department of Experimental Physics, Peter the Great St. Petersburg Polytechnic University, Russia
Corresponding author
Alexander I Melker, Department of Mechanics and Control Processes, Peter the Great St. Petersburg Polytechnic University, Polytekhnicheskaya 29, St. Petersburg, 195251, Russia.
Accepted: July 17, 2018 | Published Online: July 19, 2018
Citation: Melker AI, Vorobyeva TV (2018) Structure and Energy of the Δn = 14 Series Fullerenes. Int J At Nucl Phys 3:008.
Copyright: © 2018 Melker AI, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Fusion reactions of cupola half-fullerenes C16 + C22, C18 + C24, C24 + C32, C30 + C40, C36 + C48 are considered on the basis of Arrhenius's postulate. It means that at first there forms an intermediate compound and only afterwards a usual chemical reaction is going on. The final structure of fullerenes is obtained with the help of geometric modeling and is optimized through the use of Avogadro package. The fullerenes obtained, C38, C42, C56, C70 and C84, tend to take the appearance of a perfect spheroid with lesser formation energy. The graphs corresponding to the fusion reaction are given and the energy of fullerenes is calculated.
Keywords
Cupola, Energy, Fullerene, Fusion reaction, Graph, Modeling
Introduction
In Ref. [1,2] we have suggested the periodic system of fullerenes. It consists of horizontal series and vertical columns (groups). The horizontal series form the Δn periodicities having one and the same main characteristic feature; the fullerene structure changes from threefold symmetry to sixfold through four and fivefold ones. The vertical columns include the fullerenes of one and the same symmetry, the mass difference Δm for each column being equal to a double degree of symmetry. We suppose that these features can be taken as a basis for rigorous fullerene classification. The Δn periodicities studied consist of the following series: Δn = 6, 8, 10, 12, 14, 16 and 18, fullerenes from C14 to C108 being incorporated. For the most of series, their structure, energy and formation are discussed elsewhere. We suppose that the fullerenes of one and the same group have similar properties. The fullerene structure for the series Δn = 14 was also obtained through the use of geometric modeling, but the results were not published. In this contribution we present the structure, energy and graphs of the Δn = 14 series fullerenes. Knowing these characteristics allows one to activate the fullerene for farther investigations.
Fusion Reactions of Cupola Half Fullerenes
In Ref. [3] we have developed an algorithm that has proved itself in predicting the growth of perfect fullerenes conserving an initial symmetry, so called the fusion reaction algorithm.
Reaction between two cupolas C16 and C22
In Figure 1 the atomic configurations corresponding to reaction are shown. At first two molecules are moving towards each other (Figure 1a). Then the atoms, marked in dark-red, interact with each other producing a compound (Figure 1b). During this process new covalent bonds (heavy red lines) are being formed. As a result, a distorted polyhedron is formed which relaxes into a perfect polyhedron (Figure 1c). Its atomic configuration consists of nine hexagons and twelve pentagons, so it can be named a penta12hexa9-polyhedron.
Reaction between two cupolas C18 and C24
Similar to the previous reasoning, one can consider the atomic configurations corresponding to reaction . As before, at first two molecules are moving towards each other (Figure 2a). Then the boundary atoms interact with each other producing a distorted polyhedron (Figure 2b), which relaxes into a perfect polyhedron (Figure 2c). Its atomic configuration consists of two triangles, six pentagons and fifteen hexagons and so it was named a tri2penta6hexa15-polyhedron.
Reaction between two cupolas C24 and C32
The procedure for visualization of reaction is the same as before. The atomic configuration of the perfect polyhedron (Figure 3) consists of two squares, eight isolated pentagons and twenty-two hexagons, so it could be named a tetra2-penta8-hexa22-polyhedron.
Reaction between two cupolas C30 and C40
It is written as . The atomic structure corresponding to a perfect polyhedron (Figure 4) consists of twelve isolated pentagons and twenty-five hexagons, so it could be named a penta12-hexa25 polyhedron.
Reaction between two cupolas C36 and C48
The procedure for visualization of reaction is the same as before. The atomic structure corresponding to a perfect polyhedron (Figure 5) consists of twelve isolated pentagons and thirty-two hexagons, so it could be named a penta12-hexa32 polyhedron.
Single and Double Bonds, Energy
We assume that the symmetry of double bonds location about the major axis of cupolas and other fullerenes coincides with that of fullerene C60. Using this postulate, we have all the necessary input data for the optimization of the fullerene and cupola structures designed by means of geometric modeling and for subsequent calculation of their properties. As it was described above, the cupolas having one and the symmetry can react with each other producing fullerenes C38, C42, C56, C70, and C84 with single and double covalent bonds and, in the case of fullerene C38, with partially delocalized bonds too. The optimized structures of the fullerenes obtained through the use of Avogadro package [4] are shown in Figure 6. The energy change of the fullerenes can be explained in a similar manner as in Ref. [5].
Graph Representation and Electronic Structure
The theoretical approach to fullerenes is based on the topological and graph treatment. "The fullerene graphs contain all the information we need, and we able to sort through the millions of isomers, finding a few candidates for the most stable, by way of simple easily computed topological indices for pentagons or hexagons" [6]. At that, the authors define (classical) fullerenes as "cage-like, hollow molecules of pseudospherical symmetry consisting of pentagons and hexagons only, resulting in a trivalent (and in the most ideal case) convex polyhedron with exactly three edges (bonds) joining every vertex occupied by carbon, idealized as sp2 hybridized atoms".
Consider the graphs which characterize the formation of the Δn = 14 series fullerenes (Figure 7). From the graph representation it follows that the main difference of fullerene C38 from others is the absence of double bonds in the graph center. Therefore the electronic structure in this area of fullerene C38 differs from that of other fullerenes. In other words, fullerene C38 does not refer to classical fullerenes defined in Ref. [6]. Let us take up the situation in more detail.
In 1940 Sidgwick and Powell supposed that the geometry of a forming molecule is dictated by repulsion of valence electron pairs [7,8]. They formulated the following rule: Electron pairs arrange themselves inside the valence shell of an atom into such configuration which ensures their maximal removing from each other. In other words, the electrons pairs behave themselves as if were repelling each other similar to point charges. The assumption is in a good agreement with experimental data for more than 1500 molecules. If each electron pair present as a point and to connect the points by direct lines, one obtains the electronic configuration of chemical bonds [8,9]. Each configuration at a given number of electron pairs can create several space molecular structures. It depends on the number of binding and unshared pairs.
Consider two simple molecules, methane and ammonia. Denote a central atom of a molecule by letter A and a noncentral atom by B. Let a molecule AB4 has no multiple bonds. For four binding electron pairs, the configuration is a tetrahedron, and we have a tetrahedral molecule, methane (Figure 8). Here the atomic configuration repeats the electronic. In the case of a molecule AB3, where the valence shell contains three binding pairs and one unshared, the situation is radically different. The unshared electron pair is on a line which connects the central atom with one of tetrahedron apices. As a result, the molecule has the form of pyramid, and we obtain ammonia (Figure 8). In this case the electronic and atomic configurations do not coincide and we have so called hidden symmetry [10].
Discussion
Today there are a lot of papers on fullerene properties. Using different computational methods (there are also a lot of programs), the authors calculate the properties of the most popular fullerenes which structure is known. As a result, the numbers obtained contradict to each other and only increase disordered information. The absence of appreciable progress in understanding fullerene nature is determined by the domination of numerical calculations on the known structures. However, any numerical calculations are unable to predict new structures, so the 'numerical progress' results mainly in increasing numerical entropy. It should be emphasized that numerical calculations are not a theory, but a kind of numerical experiment [11].
As already noted the theoretical approach to fullerenes is based on the topological and graph treatment. However, it was developed only for classical fullerenes consisting of pentagons and hexagons only. Luckily there is another approach to the fullerenes (classical and non-classical), where "the fullerene is defined as any convex shape inscribed into a spherical surface which can be composed of atoms, each atom having three nearest neighbors, as in usual fullerenes, whenever discussing hollow carbon clusters" [12]. It should be emphasized that there is no restriction on the electronic structure and on the polyhedrons; they can be not only pentagons and hexagons, but also triangles, square and heptagons. Such approach allowed obtaining possible forms of mini-fullerenes from C4 and C20. At that, we have constructed graphs for all the mini-fullerenes [13,14]. The graph analysis simplifies an understanding of both the ways of fullerene growth and their structures obtained.
Consequently, the aim of research is not to do calculations for calculations, but at first to develop a system (mathematical model) as a basis for the calculations. The first step of creating any mathematical model is the formulation of the laws that connect the main objects of the model [15]. In our case the main objects are perfect basic fullerenes; we have also the preliminary law in the form of the periodic system [2] and the fusion algorithm for obtaining perfect basic fullerenes, but we do not know the structure of all the main objects. Besides, not all perfect fullerenes, the structure of which being known, are incorporated in the suggested periodic system. Therefore, the next step in our investigation is obtaining the structure and energy of missing fullerenes with the purpose to incorporate the missing known and unknown fullerenes in the periodic system. Only afterwards, having a comprehensive picture, it seems reasonable to try to explain why some fullerenes are more stable than others.

