International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 2, Issue 1
Research Article
DOI: 10.35840/2631-5017/2504
Could a Large Spectrum of Super-Heavy Elementary Particles and Micro Black-Holes be Responsible for Dark Matter?
J Michael Köhler*
Table of Content
Figures

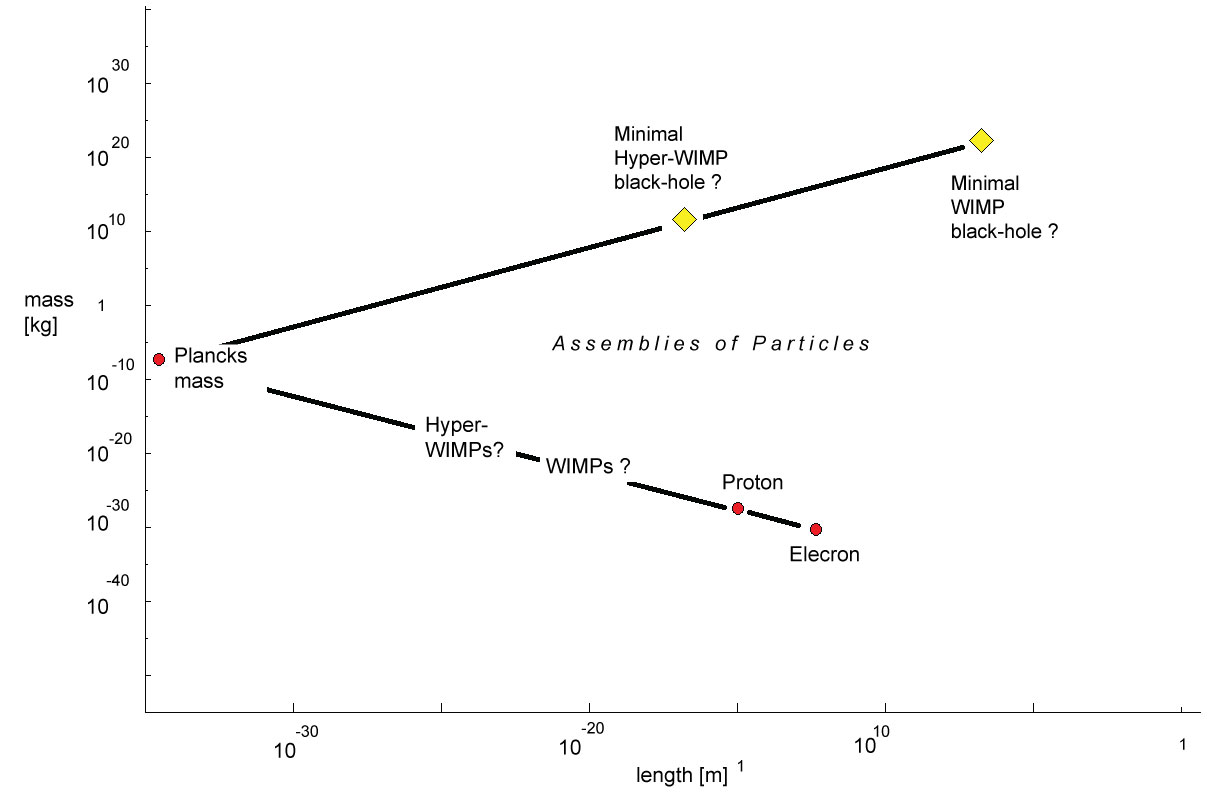
Figure 1: Asymmetry in the mass-to-length-ratios between...
Asymmetry in the mass-to-length-ratios between microscopic and macroscopic world.
Tables
Table 1: Base masses and related energies of proposed main classes of particles in dependence of the particle class-related quantum number n.
References
- Ratra B, Vogeley MS (2008) The beginning and evolution of the universe. Pub Astron Soc Pacific 120: 235-265.
- Young BL (2017) A survey of dark matter and related topics of cosmology. Frontiers in Physics 12: 121201.
- Gonzalez Garcia MC, Yosef N (2003) Neutrino masses and mixing: evidences and implications. Rev Mod Phys 75: 345-402.
- Fisher P, Kayser B, MacFarland KS (1999) Neutrino mass and a oscillation. Ann Rev Nuclear Part Sci 49: 481-527.
- Hime A, Jelley NA (1991) New evidence for the 17 keV neutrino. Phys Lett B 257: 441-449.
- Buchmueller O, Doglioni C, Wang LT (2017) Search for dark matter at colliders. Nature Physics 13: 217-223.
- Feng JL (2010) Dark matter candidates from particle physics and methods of detection. Ann Rev Astron Astrophys 48: 495.
- Lukash VN, Mikheeva EV, Malinovsky AM (2011) Formation of the large-scale structure of the universe. Phys Usp 54: 983-1005. 983-1005.
- Mohr PJ, Taylor BN (2005) CODATA: Recommended values of the fundamental physical constants: 2002. Rev Modern Phys 77: 1-107.
- J Bonn, B Bornschein, L Bornschein, L Fickinger, B Flatt, et al. (2001) The mainz neutrino mass experiment. Nuclear Physics B - Proceedings Supplements 91: 273-279.
- EW Otten, C Weinheimer (2008) Neutrino mass limit from tritium beta decay. Rept Prog Phys 71: 086201.
- Dirac PAM A new basis for cosmology. Proc Royal Soc London 165: 199-208.
- Köhler JM (2016) World out of nowhere. Leibniz Society.
- PAR Ade, N Aghanim, C Armitage-Caplan, M Arnaud, M Ashdown, et al. (2014) Planck 2013 results. XVI. Cosmological Parameters. Astronomy and Astrophysics 571: 16.
- AK Drukier, S Nussinov (2013) Towards detection of low mass WIMPs (MWimp < 10 GeV/c2): Mini review. Int J Modern Phys A 28: 1330033.
- M Drees, CL Chan (2008) Model-independent determination of the WIMP mass from direct dark matter detection data. JCAP 0806: 012.
- T Troster, S Camera, M Formasa (2017) Cross-correlation of weak lensing and gamma rays: implication for the nature of dark matter. Monthly Notices Royal Astronom Soc 467: 2706-2722.
- R Catena (2017) WIMP capture and annihilation in the Earth in effective theories. J Cosmol Astropart Phys.
- J Lundberg, Joakim Edsjö (2004) Weakly interacting massive particle diffusion in the solar system including depletion and its effect on Earth capture rates. Phys Rev D 69.
- J Angle, E Aprile, F Arneodo, L Baudis, A Bernstein, et al. (2008) First results from the XENON10 dark matter experiment at the Gran Sasso National Laboratory. Phys Rev Lett 100: 021303.
- KG Savvidy, JD Vergados (2013) Direct dark matter detection: A spin 3/2 WIMP candidate. Phys Rev D 87.
- AM Green (2007) Determining the weakly interacting massive particles mass using direct detection experiments. J Cosmol Astrophys.
- ME Krauss, T Opferkuch, F Staub, MW Winkler (2016) Soft gamma rays from heavy WIMPs. Phys Dark Universe 14: 29-34.
- JL Feng, A Rajaraman, F Takayama (2003) Superweakly interacting massive particles. Phys Rev Lett 91: 011302.
- JAR Cembranos, JL Feng, A Rajaraman, F Takayama (2005) Superweakly interacting massive particle solutions to small scale structure problems. Phys Rev Lett 95: 181301.
Author Details
J Michael Köhler*
Department of Physical Chemistry and Microreaction Technology, Technische Universität Ilmenau, Germany
Corresponding author
J Michael Köhler, Department of Physical Chemistry and Microreaction Technology, Institute for Micro- and Nanotechnologies, Technische Universität Ilmenau, PF 10 05 65, D-98684 Ilmenau, Germany, Tel: 49-0-3677-69-3700, E-mail: [email protected]
Accepted: August 30, 2017 | Published Online: September 01, 2017
Citation: Köhler JM (2017) Could a Large Spectrum of Super-Heavy Elementary Particles and Micro Black-Holes be Responsible for Dark Matter?. Int J At Nucl Phys 2:004.
Copyright: © 2017 Köhler JM. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A concept of a large spectrum of particle masses is suggested in order to discuss the problem of dark matter in the universe. Therefore, a simple scheme of particle classes can be formulated by using the Large Number Hypothesis bridging elementary and cosmological data. The proposed scheme includes a common approach for a rough distinction of groups of elementary particles, which can be distinguished by many orders of magnitudes of their rest masses. Probably, the maximal rest masses of neutrinos as well as the masses of hypothetical heavy Weakly Interacting Massive Particles (WIMPs) can be included in the scheme. Under the assumption of the elementary character of the super-heavy particles, it is proposed to assume the formation of micro-black-holes by them contributing to the missed masses.
Keywords
Particle masses, Neutrinos, WIMPs, Micro-Black-Holes
Introduction
The different evidences for dark matter [1] and its clear relation to gravitation challenge for an extension of the spectrum of regarded candidate objects. The contribution of dark matter to the total of rest masses in the universe is high [2]. The recent state of research seems to prove, that it cannot be identified simply with dark planets or star-like objects and gas clouds. Thus, there have to exist smaller particles in comparatively high density, and they have to be not to light-weight. In the past, particles showing very low interaction probability with normal matter had been under discussion. On the one hand, neutrinos [3] are present in a very high number in the universe, but a lot of investigations are speaking for the fact, that there particle rest masses are too low for explaining the whole missing mass in cosmic structures as galaxies [4,5]. On the other hand, there are evidences and searches for extraordinary heavy particles showing also a low interaction probability with normal matter [6]. But, these so-called WIMPs (Weak Interacting Massive Particles) [7] seem not to be frequently enough for filling the gap. Therefore, there is an urgent need for new concepts for strange matter in the universe. Here, it will be tried to extend the idea of WIMPs into a speculation about a larger spectrum of strange compact objects.
Masses and Length Scales
Despite the usability of models assuming roughly homogeneous properties, the universe is neither isotropic nor homogeneous [8]. Beside the homogeneity of the microwave cosmic background, the universe is dominated by structures at different length scales, from elementary particles over planets and stars up to groups of galaxies, super clusters and huge empty space bubbles. These structures correspond to a structured distribution of masses. Obviously the probability of certain masses is higher than other masses. This effect is clearly evident at least in the case of the elementary particles.
There exists a fundamental difference between macroscopic and elementary objects in relation to the ratio of masses and geometrical extension (Figure 1). Under the assumption of a nearly constant density, the size of macroscopic objects increases with their mass. This behaviour is the normal case in everyday life, if liquid and solids are experienced. It is not applicable for elementary particles, because their size has to be characterized by an intrinsic length, the Compton wave length. This length describes the physical extension of quantum objects. The characteristic lengths of these objects increase with decreasing mass linearly. For example, this is the reason for the fact, that the heavy neutrons are much less extend and compacter than the light electrons.
Hypothetical Classes of Elementary Particles
The comparison of rest masses of "normal" elementary particles with the maximal rest masses of neutrinos and the probable masses of the hypothetical heavy WIMPs makes clear, that there is a gap of several or even many orders of magnitude. All particles of baryonic matter can be regarded as one group of particles with rest masses in the same order of magnitude. Neutrinos and probably WIMPs are distinguishable by their possible masses from this group.
Up to now, there is no closed theory explaining the amount of particle masses. The only reference mass from theory is given by Planck mass [9]. This mass is about 20 orders of magnitude larger than the mass of baryons and about 30 orders of magnitude larger than the upper limit of the rest mass of neutrinos [10,11]. In the following, a rough proposal will be given, how the order of magnitude of masses of baryons and the expected possible rest masses of neutrinos can be broad into a relation to Planck mass. Therefore, a simple quantitative relation using the "Large Number Hypothesis" (LHN) is proposed. The idea behind this speculation is the assumption that different classes of elementary particles exist which can be distinguished by their energy or masses. It is assumed that these particles have the character of quantum objects and can be related to different parts of the broad energy/mass spectrum reaching from extreme low-energy photons up to a quantum object of the size of a Planck mass.
The LHN-Hypothesis was formulated by Paul Dirac already, who recognized a quantitative relation between cosmic numbers and numbers in the world of elementary particles [12]. Thus, the order of magnitude of the size of the universe is approximately 1040 times larger than the diameter of a nucleon. The application of this concept to the Planck scale [13] spans about 61 orders of magnitude. A characteristic ratio z can be formulated between the product of vacuum light velocity c and the inverse Hubble constant (1/H) and Plancks length Lp:
With
This ratio z can be interpreted as the number of elementary time intervals (Planck time tp) from the beginning of the cosmic evolution up to now. Equation (2) reflects the interpretation of the Hubble constant by the inverse age of the universe. The number z can be understood as a cosmological parameter.
The hubble time tp is directly related to a fundamental energy, the Planck energy Ep:
This energy can be expressed either by the fundamental Planck time, by the fundamental Planck mass mp or approximated by the number z and the Hubble constant as described by eq. (3).
It is striking, that the ratio of Planck mass to the mass of nucleons is in the order of magnitude of 1020. This number corresponds roughly to the cubic root of the cosmological ratio z, which was introduced above. The following table is based on the speculation that the root exponent n can be regarded as a quantum number and that this number defines the order of magnitude of particle masses in particle classes which are related to one of these quantum numbers. The Planck mass is used as the fundamental base mass in the form
Instead of the usually applied Planck mass in the form of
Then a set of energy classes and mass classes can be formulated by using a quantum number n and a simple approximation for base masses in dependence on this quantum number and the universal incremental counter z:
This arbitrary, but very simple formulation supplies a good approximation for the mass of nucleons for n = 3. Other base masses are obtained by this equation (6) using for lower and higher number n, what means different roots of z (Table 1):
The absolute numbers in the table are only rough approximations and related to the estimation of z ≈ 8*1060, a number which might be corrected moderately in the future. The first class (n = 1) is related to photons. The extreme low mentioned energy describes the energy of a thought photon with a wave length corresponding to the diameter of the universe. Such photons are not localized, but omnipresent. Each other photon can be regarded to have a wavelength of a fraction of these lowest-energy photons. The particles of this class have no rest masses. The second class of particles (n = 2) is related to very low rest masses. It is not clear if these particles are really neutrinos, but the approximated value is not very far from the estimated upper limit of neutrino masses. The third class (n = 3) is related to standard elementary particles as protons and neutrons (Figure 1). Likely, electrons have also to be related to this class despite their much lower weight. The particles of the forth class (n = 4) should be found at considerable higher energies and have probably high rest masses. They could be related to the hypothetical WIMPs (Weakly Interacting Massive Particles). These particles are described to have particle energies between a few [15], some tens [16-18] and hundred or more eV [19-21]. In some cases, energies around 0.5 keV have been discussed [22,23]. It has to take in account that the measured energies might be only a part of the total energy of impacting WIMPs, what means that energies and rest masses of these particles are not completely converted into energy of other particles in case of impacts or collisions. It should be thought about certain probability that highly accelerated WIMPs might pass the whole diameter of earth-analogously to neutrinos, or slower WIMPs can be trapped by the gravitational field of earth and are either populating orbits or are penetrating the earth crust and mantle and fixed in the center of our planet. In this last mentioned case, it is likely that most heavy cosmic bodies-as stars, planets and moons-have a core of accumulated WIMPs. A group of particular heavy WIMPs is postulated in the frame of the drawn picture of particle classes for n = 5 and higher numbers. They are named here "Hyper-WIMPs" in order to avoid a confusion with the term of so-called "Super-WIMPs" [24,25], which are marked by particular low interaction. The energy distance between the hypothetical particle classes decreases with increasing number n. That means that above a certain number (n >> 5), a more or less continuous spectrum of super-heavy particles could be expected.
Assemblies of Particles
Beside black holes, the densest packaging of baryons is found in the nuclei of atoms and in neutron stars. A rough estimation of density of neutrons ρN is given by the Compton wave length λN, their related volume (approximated by a cube: VN = λN3) and the mass mN of neutrons:
(h = Planck's constant, c = velocity of light)
In principle, WIMPs and Hyper-WIMPs should have also the ability to aggregate. In analogy to the density of baryons in nuclei and neutron stars, very dense objects could result, if the postulated heavy objects are elementary particles. Their density can easily be approximated by the assumption, that their volume VWIMP can also be derived from a characteristic particle diameter λWIMP, which can be understood as the Compton wave length of these particles
Supplying:
Very high densities would appear for Hyper-WIMPs (n = 5 or higher):
These huge densities mean that black holes are already formed for comparatively low particle numbers, what means in case of small and light-weight aggregates (Figure 2). In the most extreme case, a particle with the Planck mass (5.45*10-8 kg) results. It has a size of 4*10-35 m and forms the smallest imaginable black hole.
Conclusions
It is proposed here to think about a large spectrum of elementary particles following a simple general classification by order of magnitude of mass. Such a classification could be constructed by the use of the Large Number Hypothesis which tries to connect cosmological parameters with particle dimensions. In particular, it is based on the fact that the ratio of Planck mass to the rest mass of nucleons corresponds roughly to the third root of a universal incremental counter z which can be identified with the ratio of the age of universe to the Planck time.
The postulated spectrum of particle classes could include in a rough scheme neutrinos and WIMPs beside the baryonic matter. In addition, it allows the existence of extreme heavy elementary particles (Hyper-WIMPS) up to the Planck mass and decreasing particle size down to the Planck length. Under the assumption of the elementary character of WIMPs and Hyper-WIMPs, they should have the ability to form super-dense aggregates and micro-black-holes. Aggregations of such super-heavy particles should not only to be find in the centres of galaxies and globular clusters, but also in smaller compact objects as stars, planets and moons.