
International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 1, Issue 1
Original Article
DOI: 10.35840/2631-5017/2502
Quantum Optimal Control for Particles at Cross-Section in Nucleus
Quan-Fang Wang*
Table of Content
Figures
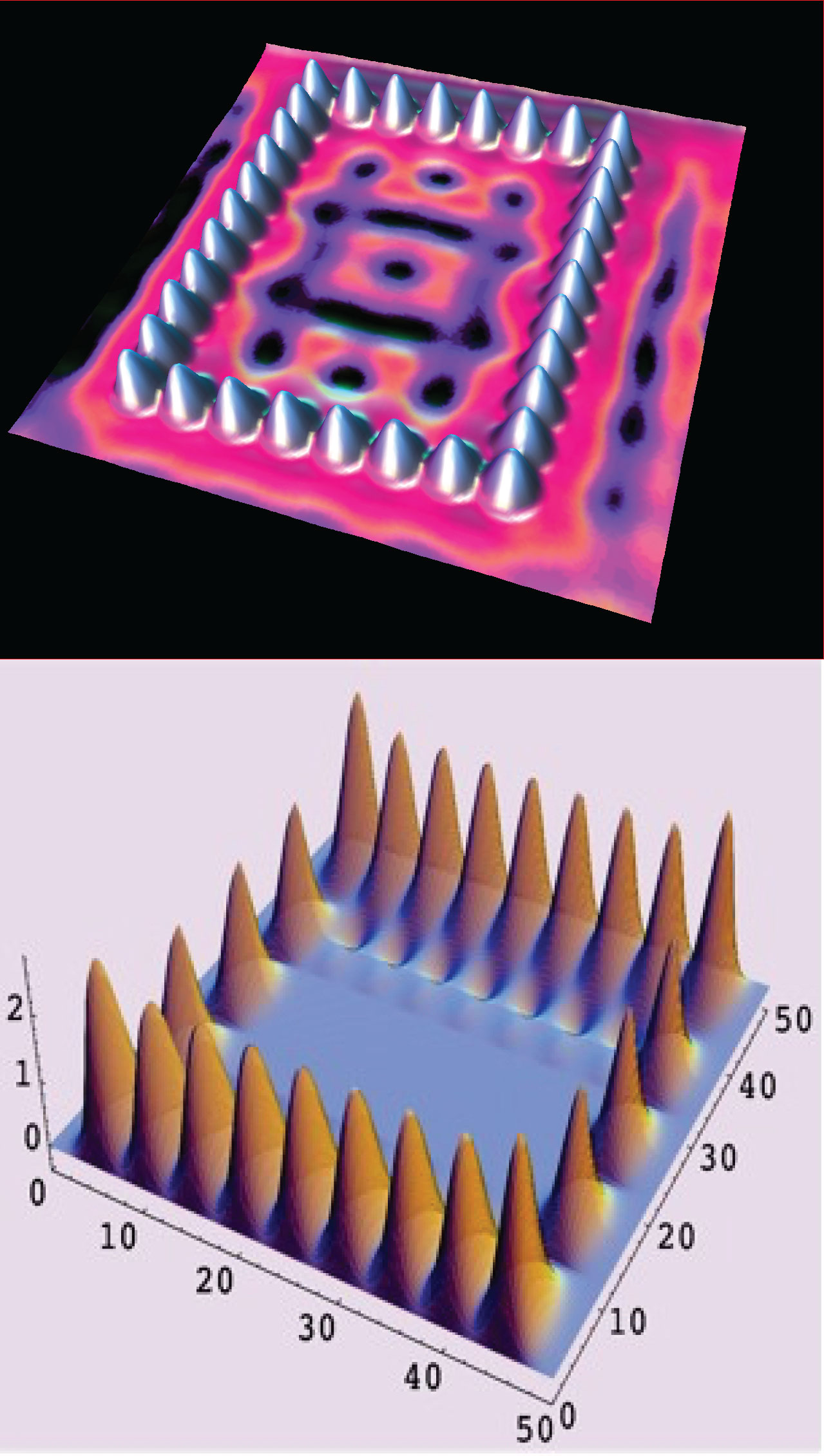
Figure 1: (A) STM image of corral, iron (Fe) on copper Cu(111); (B) Compute result of corral in [7].
(A) STM image of corral, iron (Fe) on copper Cu(111); (B) Compute result of corral in [7].
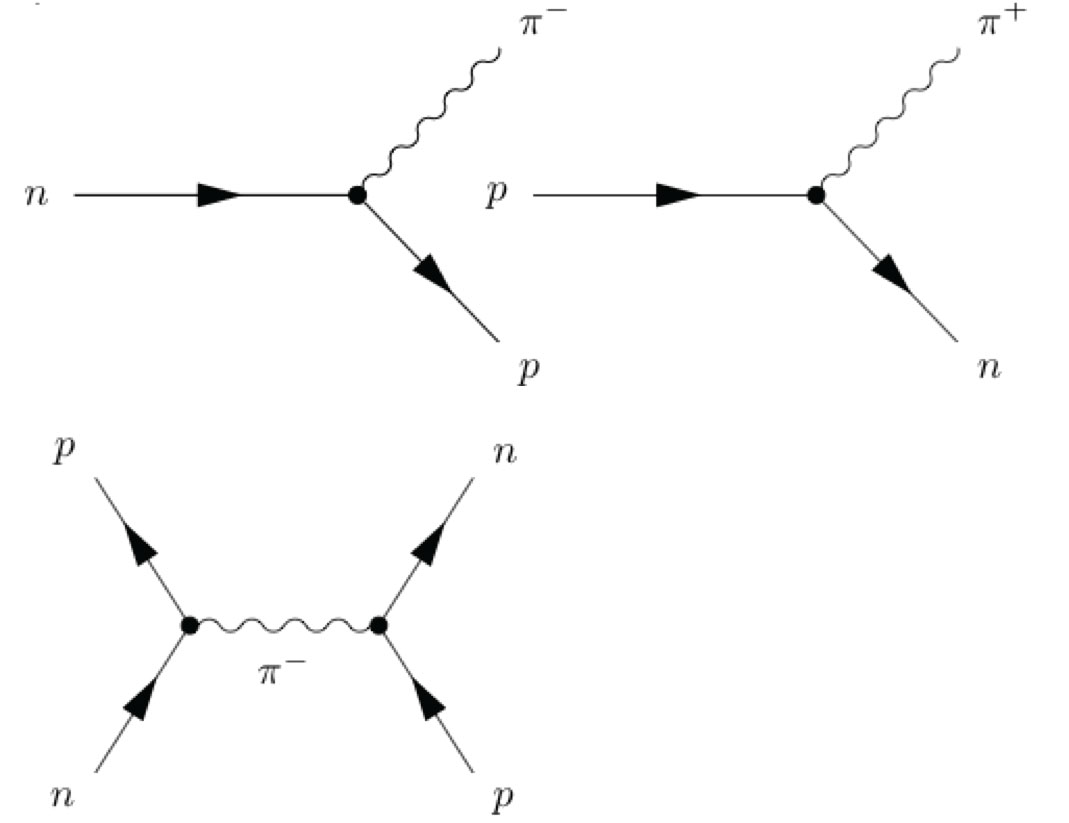
Figure 2: (A) Neutron n, proton p interactions (from left to right); (B) Meson π...
(A) Neutron n, proton p interactions (from left to right); (B) Meson π - exchange among neutron n and proton p (from bottom to top).

Figure 3: Plots of 45 nucleons ψj(t, x) at per iteration k under control uk(t),
Plots of 45 nucleons ψj(t, x) at per iteration k under control uk(t), k = 1, 2,..., N. Any of up-peaks is expressing the probability of a quantum dot (particle) at the cross-section σ in the nucleus.
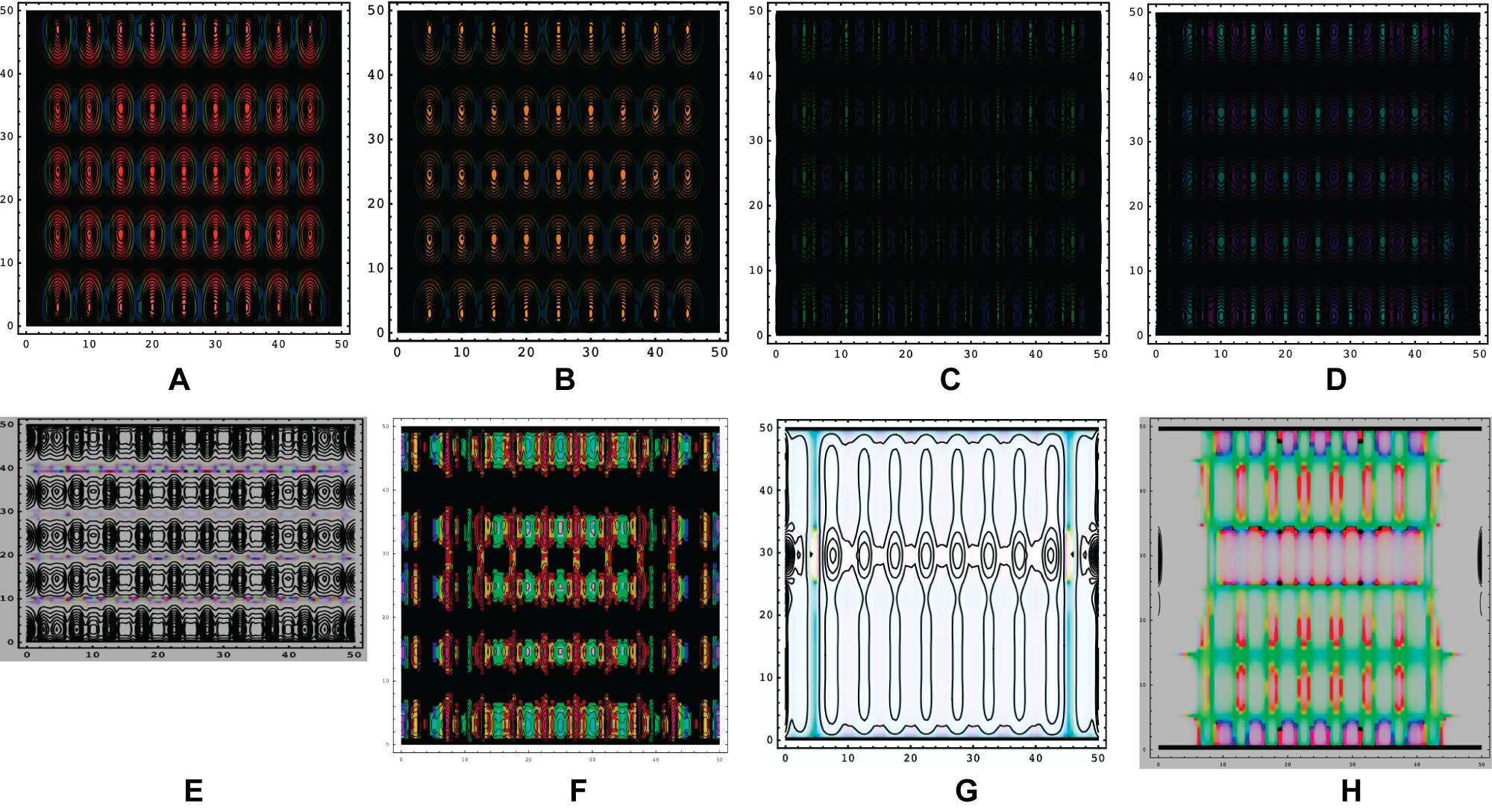
Figure 4: Contour plots of 45 nucleons ψj(t, x) at per iteration k under control uk(t),...
Contour plots of 45 nucleons ψj(t, x) at per iteration k under control uk(t), k = 1, 2,..., N. One circle is expressed a contour plot of a particle.
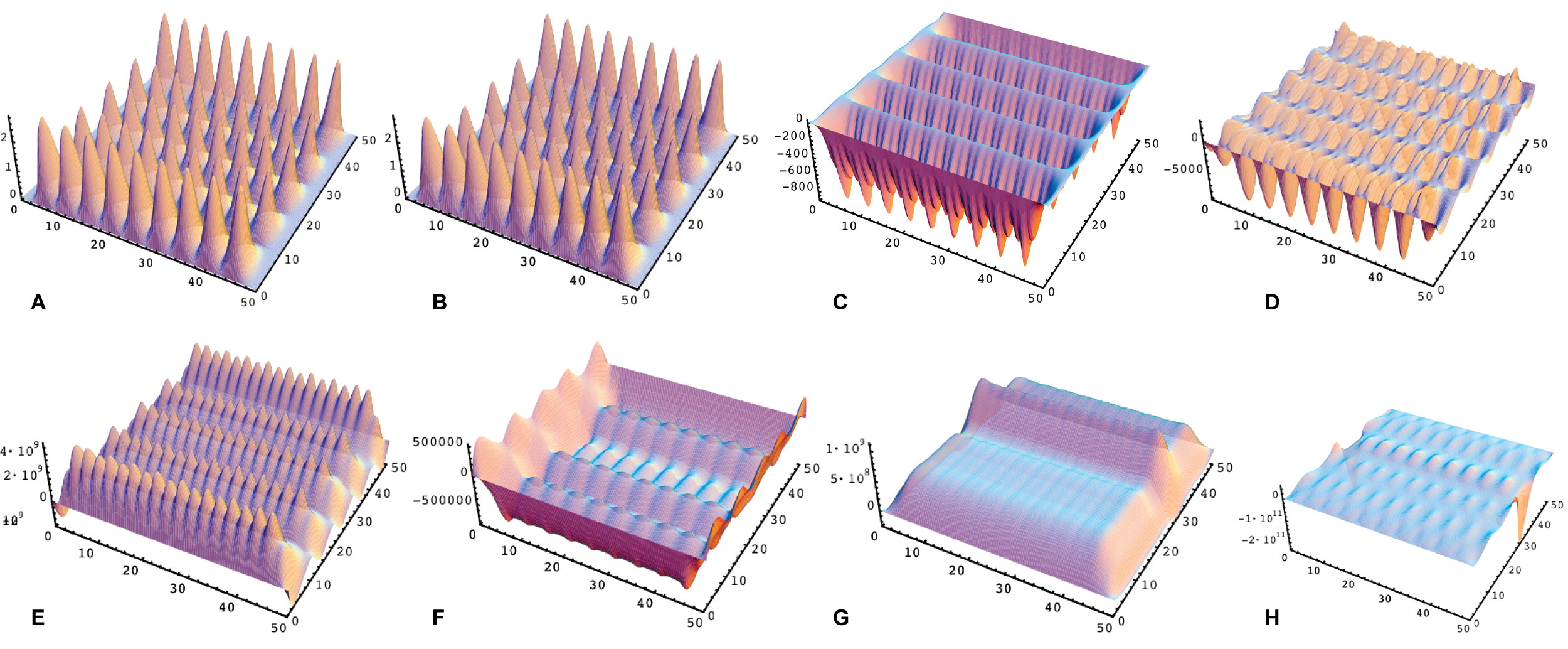
Figure 5: Plots of 45 mesons φj(t, x) at per iteration k under control vk(t),...
Plots of 45 mesons φj(t, x) at per iteration k under control vk(t), k = 1, 2,..., N. One up-peak or down-peak is representing the probability of a particle at cross-section σ in a nucleus.
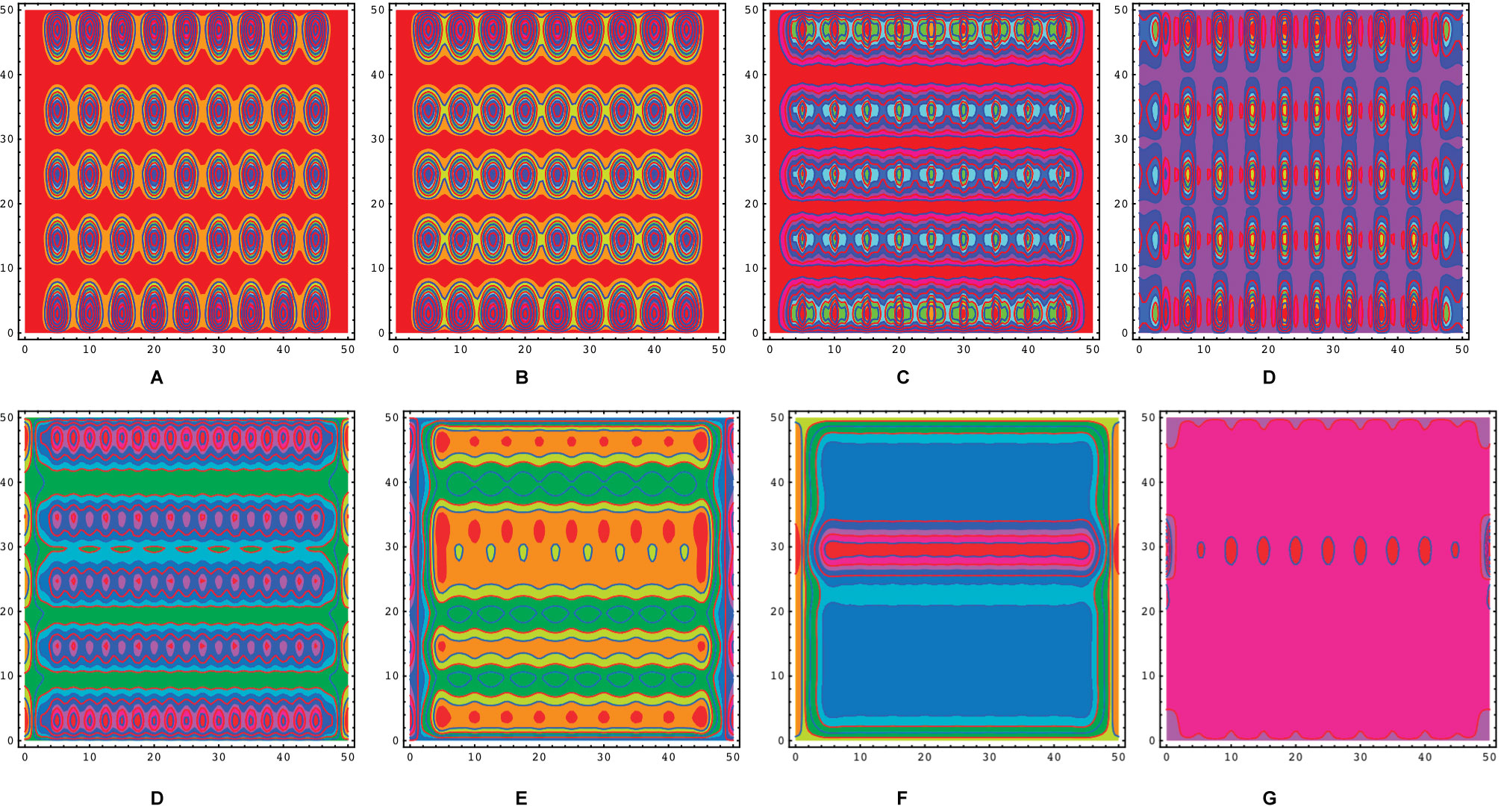
Figure 6: Contour plots of 45 mesons φj(t, x) at per iteration k under control vk(t),...
Contour plots of 45 mesons φj(t, x) at per iteration k under control vk(t), k = 1, 2,..., N. As k ≤ 5, one circle is representing a contour plot of a particle appeared at interaction of Yukawa coupling in cross-section σ at nucleus. After k ≥ 6, the probability is tend to unbounded, all the particles blow up (or escape) from the cloud of neutron as time increasing.
References
- Somorjai GA (1994) Introduction to Surface Chemistry and Catalysis. John Wiley & Sons, New York-Chichester-Brisbane-Singapore.
- www.nobelprize.org/lecture/Higgs/Gertl.
- Herschel Rabitz (2003) Shaped Laser Pulses as Reagents. Science 299: 525-527.
- Wang QF (2006) Quantum optimal control of nonlinear dynamics systems described by Klein-Gordon-Schrodinger equations. Proceeding of American Control Conference, 1032.
- Wang QF, Rabitz HA (2007) Quantum Control of Light and Matter. Gordon Research Conference.
- Wang QF (2008) Chemical Control on Electrons and Photons. European Science Foundation research conference.
- Wang QF, ACS National Meeting & Exposition, Poster (2009), Poster (2010), Poster "Presentations on Demand' (2013).
- Yukawa H, Japan Physics and Mathematics Society 17, 48 (1934). 19, 14 (1937). 20, 24 (1938). 20 46 (1938).
- Dirac P (1954) The Principles of Quantum Mechanics. Oxford Press, London.
- Lopes JL (1950) The Nucleon Magnetic Moment in Meson Pair Theories. Physical Review 78: 36.
- Schrödinger E (1952) Letters to nature. Nature 169: 538.
- Eidelman S, Hayes KG, Olive KA, Aguilar-Benitez M, Amsler C, et al. (2004) Review of Particle Physics. Physics Letters B 592: 1-5.
- Cross-section_ based quantum control is said as 'Quantum nucleus control'.
- Wang QF, Nakagiri S, Preprint of Annual Conference Japan Society for Industrial and Mathematics, 59 (2009).
- Lions JL (1971) Optimal Control of Systems Governed by Partial Differential Equations. Springer Verlag, Berlin-Heidelberg.
- Adams R (1975) Sobolev Spaces. Academic Press, New York.
- Dautary R, Lions JL (1992) Mathematical Analysis and Numerical Methods for Science and Technology. Springer Verlag, Berlin-Heidelberg.
- Temam R (1988) Infinite-Dimensional Dynamical Systems in Mechanics and Physis 68. Applied Mathematical Sciences. Springer-Verlag.
- Kostin MD (1987) Derivation of the Hamiltonian form of the Klein-Gordon equation from Schrödinger-Fürth quantum diffusion theory. Physics Letters A 125: 451-455.
- Wang QF (2010) Quantum Control in Nuclear Reaction. Int J Mod Phys E 19: 393.
- Heisenberg W (1952) Production of Mesons as a Shock Wave Problem. Phys. Bd. 133: 1-17.
- Rice SA, Zhao M (2000) Optical Control of Molecular Dynamics. John Wiley, New York.
Author Details
Quan-Fang Wang*
Mechanical and Automation Engineering, The Chinese University of Hong Kong, Shatin, NT, Hong Kong
Corresponding author
Quan-Fang Wang, Mechanical and Automation Engineering, The Chinese University of Hong Kong, Shatin, NT, Hong Kong, E-mail: [email protected]
Accepted: April 25, 2016 | Published Online: April 28, 2016
Citation: Quan-Fang Wang (2016) Quantum Optimal Control for Particles at Cross-Section in Nucleus. Int J At Nucl Phys 1:002.
Copyright: © 2016 Quan-Fang Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this work, a novel concept abstract surface (cross-section at nucleus) is proposed firstly. Quantum optimal control is interested in taking particles at Yukawa interaction of cross-section σ in the nucleus as target for controlling by external force. In the nucleus, as intersecting surface full of particles can be considered for applying control theory and numerical simulation using a stable semi-discrete algorithm. Theoretical investigation, computational approach and experimental demonstration had accomplished.
Keywords
Quantum control, Nucleus, Cross-section, Klein-Grodon-Schrödinger equation
Introduction
At the chemistry and physical fields, particle at matter (e.g. crystals, metal,...) surface had been researched for properties in chemical reactions. For instance, monolayers structure of a surface [1]; phase polarization control via coherent laser is understood by computational ability of supercomputer; control of electromagnetic radiation for plasmas design; optimization of 3D crystals to control electromagnetic field; and so forth. One of the achievements is awarded the Nobel Prize 2007 in chemistry [2] for Haber-Bosch process. Obviously, these outstanding contributions are laying on experimental methodology. On the other hand, quantum control in theory and in lab experiments are rapidly growing in a variety of fields, see previous papers [3-7]. It had already being stepped forward to control elementary particles at nucleus. Lasting striving must boost the appearance of breakthrough soonerafter. Meanwhile, a few contributions on control of particles as they are on the surface. One extremely interesting topic in here is focus on many-body problem at surface [1]. The objective particles can be regarded as electrons, nano-particles, atoms and molecules at a practical matter surface [1,5,8]. For example, observing Scanning Tunneling Microscope image, rectangular corral in Figure 1A is representing quantum dots at a metal surface.
Poster [7] was to control of many body problem of elementary particles at corral of matter surface. Theoretical and computational issues had been surveyed for two dimensions case. Comparison to Scanning Tunneling Micropscope (STM) images had evidenced of quantum control efficiently. The aim of [7] was to change the state of particle using external sorcing, such as electromagnetic field, Ti: Sapphire shaped laser, and ultra-short terahertz (THz) pulse. Cpm[utational approach of [7] is in (B) of Figure 1. As a attempt effort, numerical control approach is feasibly and flexibility in optical manipulation of quantum particles [9] at a practical surface.
In this article, the goal of quantum control is to originally propose the particles at abstract surface (intersecting surface) of a cross-section in nucleus. Not only theoretic investigation but also computational approach are executed for spatial dimension of two using a convergent numerical algorithm. The motivation is to apply quantum control theory to abstract surface science firstly, and illustrate proposed multi-body control theory by numerical experiments.
Lasting of decade study on control of nuclei, overwhelming the hesitation and difficulty, it is a surprising turning-point to find an entrance to pursue control of particles motion at cross-section in nucleus aided of basic physical concepts.
Many Body Physical Model
To deduce a rational physical control model for many-body Klein-Gordon-Schrödinger (K-G-S) dynamics system, full access for no control case can be found at Yukawa's contributed works [8]. In here, it is to capture concerned matter for determining control. Citing [10], and with outing lost of generality to consider x = (x1,x2,x3) ∈ 2 R3, the governing system of 2n particles (nucleon ψj , meson φj, j = 1, 2,..., n) in the Yukawa interacting dynamics is
Here , and are Pauli matrices, , m is meson mass, g is coupling constant for interaction of meson and nucleon (g is 1 ~ 10 fm, 1 fm = 10-15 m). is momentum operator of a nucleon, , where and are the masses of a proton and a neutron, and The equation (1) represents Klein-Gordon equation for a particle φj in an external potential produced by nucleon field φj. In general, Klein-Gordon equation for a particle in electro-magnetic field takes the form of
where is a vector potential of electro-magnetic field. The equation (2) can be regarded as Schrödinger equation [11] for a particle in an external potential produced by meson field φj. In particular, a standard way to introduce electro-magnetic interaction is by replacing in the figure brackets and adding the term , where μ is magnetic moment of the particle and H is magnetic field. Hence, these given coupled equations for interacting mesons and nucleons in an external electromagnetic field:
where e and e' denote charges of corresponding neutron and meson. To access the physical quantities, cite [9] and [12]. Further, meson charge e' = e for π+ and e' = -e for π- as in Table 1. Thus, one can attain free (uncontrolled) K-G-S system via the formulations (1) and (2), or (3) and (4) if set .
If two Hamilton operators in K-G and S systems are denoted as , respectively. Then, in non-relativistic limit regime 0 < ε < 1 case, dissipative and damped Klein-Gordon-Schrödinger system can be deduced
where and are the external potential of Hamilton operators, which given by coupling and external control forces. α is dissipative constant, γ is damped constant. Therefore, in the O(1) order speed of light regime ε = 1, the control model for K-G-S system of ψj and φj has the form of
where u and v represent the external controlling inputs, and j = 1, 2,..., n.
Quantum control is interested in taking particles at Yukawa interaction of cross-section in nucleus as target. It is a convenient way to supply the arguments on cross-section in nuclear physics as background preparation. In atomic physics, cross-section indicates the probability that a particular interaction taking place among particles. The value of cross-section for any interacting process is depending on the particles under bombardment and upon energy of bombarding particles. Suppose n particles per second are incident on a target area Ω containing N particles, and there are nr of the incident particles produce a given nuclear reaction. If nr < n, then nr = nNσ/Ω, where σ is the cross-section for the reaction; σ can be regarded as a disk of area σ surrounding each particle. The unit of effective cross-section area of nucleus is barn, and one barn equal to 10-28 m2. To elementary particle, nucleus radius (or Bohr radius) is closely to 1.2 × 10-15 m times cube root of nuclear number, or atomic mass. Cross-section unit barn is enough to measure the likelihood of one kind of particle interacting to another, especially the chance of a neutron being captured by causing fission in a nucleus. It could be considered as an area centered on a nucleus; the bigger the area, the greater the likelihood of the neutron being captured. The number of barns is determining of fission or capture cross-section. Neutron capture cross-sections can range from 0.01 to millions of barn [mb]. A view supporting by the extension of a unit of cross-section is shed, it equal to 10-24 barn. In Table 1, fundamental physical constants are inclusive for elementary particles.
K-G-S Control Problems
Consider particles appeared at a cross-section σ of abstract surface in nucleus [13]. Despite of particles at cross-section, theoretic discussion is not limited to two dimensions. Let Ω be an open bounded set of R3 and Q = (0, T) × Ω for T > 0. Thus, for x = (x1, x2, x3), (t, x) ∈ Q. Suppose 2n particles involving Yukawa interaction [8] at a cross-section σ in nucleus, hence, Klein-Gordon-Schrödinger many-body dynamics is taking the form of
where ħ is reduced Planck constant. M is mass of nucleon, and m is for meson. c is speed of light, i is imaginary part unit of scalar complex space â„‚. Coefficients α, γ are positive constants at dissipative and damped terms. A complex-valued function ψj(t,x) represents probability of j-th nucleon field, and a real-valued function φj(t,x) represents that of j-th meson field for j = 1,2,....,n. Here in (6), e and é denote charge of a nucleon and a massive meson, respectively. Physically, in the case of j = 1, two-body system (6) express neutron n (consist of quark combination udd) exchanging meson ū is anti-u quark, anti quark of u quark): or using Feynman diagram in Figure 2 for their interactions [14].
In this work, K-G-S model (6) represents a many body dynamics full of n nucleons and n mesons at Yukawa interaction on a cross-section σ in nucleus. In particular, cross-section is probability for particles taking place at chemical reaction or physical interaction. At one moment t, control attention is the particle at a certain cross-section (intersecting surface). It is a kind of abstract surface (plane or curved). Theoretically, time depended controls u(t) and v(t) are corresponding to external ultra-short (e.g. femtosecond/attosecond) laser pulses in real lab, or specially indicating external force, such as control rod in nuclear fuel of neutrons reaction for uranium 235U. More precisely, in the case of chain reaction for neutrons from nuclear fission of uranium. The moderator is to reduce the energy of neutrons and no capture many of them. In other words, neutrons need to react and change direction on colliding to nucleus and release energy, but not include fission. Not lacking of generality, carbon, beryllium, water and heavy water as mutated moderator. The control rod, inserted in moderator such as boron 5B and cadmium 48Cd, had the ability to absorb the neutrons effectively.
Inspired by neutrons chain reaction, it is clarifying to steer quantum control at nuclear scale by concentrating on particles at a cross-section σ in nucleus.
At cross-section σ of nucleus, to do mathematical setting for K-G-S many body model (6). Denote u = (u, v), and quantum optimal control u*(t) = (u*(t), v*(t)) for K-G-S system (6). Assume V = L2(0, T) is control space of u(t), v(t). Rigorously, if taking superposition of control pulse uj, vj corresponding to ψj and φj as control source (laser), it is exclusive in this scope, see theoretic results in [14] for multi-body of neutrons, protons and mesons separately. In contrast, a unified control for one type of particles is assumed in here for supposing all particles by a certain control source. In domain Ω ⊂ R2, for real-valued function φj(t, x), introduce two Hilbert spaces H = L2(Ω) and with usual norms and inner products [15]. Thereby, Gelfand triple spaces V↪H↪V' are continuous, dense and compact. is dual (conjugate) space of V. For complex-valued function ψj(t, x), define complex spaces ð•ƒ2(Ω) and corresponding to L2(Ω) and for φj, respectively [16]. Denote ð•ƒ2(Ω), and inner product for Then, induced norm
Denote
Then induced norm Surely ð•ƒ2(Ω) and are equipped as Hilbert spaces. Set â„ = ð•ƒ2(Ω) and ð• , â„-1 = = ð•* is the complex conjugate (dual) space of ð•Â. Actually, (ð•Â,â„) is a complex Gelfand triple spaces ð•â� ª â„â� ª ð•â€² two embeddings are continuous, dense and compact. Time depended controls u, v ∈ L2(0, T) to ensure avoid assumption on u(t, x), v(t, x) of nonsense, multiplied control terms to make well-posed in (6) and meaningful in practice.
For each particle ψj or φj, j = 1, 2, . . . , n at cross-section σ (take ), apply control theory to quantum system (6) in the framework of variational method in Hilbert space [4,17]. Denote all particles probabilities as ψ = (ψ1, ψ2, . . . , ψn), φ = (φ1, φ2, . . . , φn ) and analogous notations.
If ground states ð•Ân, φ0 ∈ Vn, φ1 ∈ Hn, then for control u(t) ∈ u at arbitrary time t ∈ (0, T), above setting to assure that there exist a weak solution (ψ(u), φ(u)) belonging to solution space
ð•'n,
for
and satisfy
such that μ(T) = v(T) = vt(T) = 0 a.e. in t ∈ [0, T]. From Sobolev space [16] to imply Definition of W(0, T) is well-posed for and in (6) and weak form (7) too. It means that one wave packet ψj can represent one nucleon (n or p), and another wave packet φj can represent one meson (π+ or π -). The details interpretation in the equation (6). Qualitatively speaking, those solutions ψj, φj are sufficiently smooth.
Control Theory for Particles at Cross-section
Start quantum nucleus control [13]. Suppose is the space of controls u [18], let be a admissible set of For particles n involved in Yukawa interaction at a specified cross-section quadratic cost criteria function of K-G-S many-body system (6) is described by
where are target states, are observed final states at time tf, respectively. In here, ∈1 and ∈2 are weighted coefficients for balancing the values of inherent cost and running cost. is observation operator, and is positive systemic operator, in details In practice, acquired essential task is to measure target states and final states constrain control source u, just like to tailor control rod at proper temperature for a nuclear reactor. Notice that we can do adjustment and confinement for maximum or multi-propose control objective.
Two fundamental problems of quantum optimal control theory is to find and characterize quantum optimal control u* = (u*, v*) such that
Theoretically apply quantum control theory [4] to K-G-S many body system (6) to result that: at a cross-section σ in nucleus, for each particle if given ground state and is closed convex (bounded) subset of Then, there exists at least one quantum optimal control u* = (u*, v*) for Klein-Gordon-SchrÓ§dinger manybody system (6) subject to quadratic criteria function (8). The solution mapping is continuous. Quantum optimal control u* = (u*, v*) is characterized by simultaneously optimality system (Euler-Lagrange system) as:
Where is the conjugate (adjoint) operator of is canonical isomorphism on H. are weak solutions of adjoint system (10) corresponding to solution in (9), respectively. It is well known that inequality (11) is the optimality necessary condition of quantum optimal control u* = (u*, v*).
For Lagrange principle energy calculation, using vector to write K-G-S many-body system (6) for one j-th particle in matrices as
Then for cost function (8), Lagrangian function of many body K-G-S control model 960 is generally in the form of

In here, are conjugate spaces of ð•n, Vn, and p* ∈ Vn, q* ∈ Vn, are conjugates of ψ, φ, ψ(0), φ(0), φt(0), respectively. For practical calculation, take the form of integral of scalar product of duality, or take real part of complex function, and regard the dual of conjugate spaces as inner products of H by Gelfand tripe spaces for effective values. Physical properties can be evaluated for Hamiltonian [19] function H(t) is in the form of

Here, p ∈ ð•n, q ∈ Vn, qt ∈ Hn are solutions of adjoint system corresponding to ψ ∈ ð•Ân, φ ∈ Vn, φt ∈ Hn of K-G-S system (6). For given ground states ψ0, φ0, φt, Hamiltonian function only depended on time t. Thus, from a start time t0, the trajectory for one particle can be tracked and attain optimal control u* by
Notable that, if needing consideration of special curved surface inside a matter or metal, abstract surface concept would be well-posed as extension. Vice versa, in practice, taking a real problem as abstract surface or dealing as boundary problem, it is credible case by case. Comprehensively, in controlling of nuclei, it is good at adopting cross-section as abstract surface.
Computational Approach
At the view point of physics, for practical formulation and plots of a cross-section, refer to section 39-40 in distinguishing paper [12]. For multi-body decay or collision, the calculation for mass of effective particles is extensively discussed in section 38 [12] in the case of production of n-body final state. The differential expression of a cross-section of two-body is worked for uncontrolled particles. Neglecting details quantitative calculation in here. This work is to introduce the concept of abstract surface to surface science and quantum control fields. Cross-section as a concept is captured as one example of abstract surfaces theoretically. Of course, all the property of a physical cross-section is working for the extended case of control purpose. It is a tough task to fill the gap, and make the interface from inside atomic structure to abstract surface and quantum control.
Reviewing the successful algorithms for optimal control in the area of quantum system, the significant ones are iteration learning algorithm [3], genetic algorithm, evolutional algorithm. Former paper [20] is for case of n = 2 quantum control typically. In this paper, for finding quantum optimal u*, a reasonable semi-discrete algorithm (spatial variable x discrete, time t continuous) is employed for controlling many-body dynamics at a cross-section σ of nucleus. The wave-particles duality and uncertainty principle [21] permit the ideal and reliable scheme. Finite element method and nonlinear (updated) conjugated gradient method composed a convergent numerical paradigm, refer to [4,6,7]. The convergence is guaranteed in the first order. To avoid complication, take real atomic scale as Table 1 in computing. Roughly set M = Mn = Mp = 1, α = γ = 0, m = ħ = c = 1, g = 1 and parameters setting for visualization effect. Fortunately, because of particles at abstract surface, it is appropriate and enough to consider two-dimensional case for spatial variable. Set X = Y = 50 μm, spatial domain Ω = (0, X) × (0, Y), or regularization as disk of cross-section σ. Set center location Time duration (t0, T), start time t0 = 0.0(fs), iteration number N ≤ 8, dt = 0.5, then iteration step t = ndt (fs), final time T = Ndt (fs). Define appendix functions for initial states configuration.
Where x' ∈ Ω is spatial variable, v1 and v2 are velocities (a.u. m/s) of nucleon and meson. Set v1 = -5/6 and v2 = 5/6. Gaussian enveloped function then initial control functions (intensity unit W/cm2) are u1(t) and v1(t), defined in the form of and for k = 1, 2,..., N. Rabi-frequency are 300,100(GHz) for uk, and 240, 450 (GHz) for vk. For j = 1, 2,..., n and j = i + 9(k - 1), initial ground states is taken as
For two dimension domain Ω, total particles, 45 nucleons and 45 mesons, are in a cross-section σ at nucleus as control target. Take coefficients and in cost function (8). Therefore, by limited iteration steps, simulating probabilities of nucleons ψj(t; x) at cross-section σ in nucleus are listed in Figure 3. The amplitude of ψj are changing from scale 2 a.u. to 1023 a.u. (Notice that if taking amplitudes of initial controls as 10-24, by converting, final amplitude is to 10-1, all the normalizing probability ψj < 1 for 1 ≤ j ≤ n, it is a good agreement to physical result).
In the mean time, for above particles, corresponding contour plots of nucleon ψj(t; x) refer Figure 4 at same atomic scale of spatial x. Changing of the probabilities is for all particles as time varying.
Similarly, simulation results for probabilities of mesons φj(t; x) at cross-section σ in nucleus are given in Figure 5. Clearly, from positive to negative, the probability of meson is changed dramatically than that of nucleon. Finally, the amplitude of φj are changing from scale 2 a.u.to -1011 a.u. (Analogously, normalizing initial controls to 10-24 gauge, converted amplitude of meson φj from 10-24 to final 10-13, it is close the neutron radius (1), the right distance for meson into or escape from a neutron at a cross section σ if the meson in the cloud of the neutron. Clearly, all the probability φj < 1 for 1 ≤ j ≤ n, and cross-section σ is a confidence region as precise measurement).
From Table 1, meson mass m ≪ nucleon mass M (pion π mass is 0.148 times proton mass). The influence of external force is greater on mesons than on nucleons. Certainly, it is coincide to physics experiments. At each iteration, one can find corresponding contour plots of φj(t; x) in Figure 6 for mesons changing as time increasing.
At natural, through the matched simulation, particles transfer momentum and energy from one to another. Cost function at each step is calculated as J = (1148.82, 1090.29, 2.60404 × 108, 1.24037 × 1010, 1.15821 × 1022, 7.17372 × 1014, 7:22776 × 1020, 5.17419 × 1023). Optimal cost value J(u*) = 1090.29 a.u. for minimum of two terms in cost function (8), cost error is estimated as 58.5312 a.u. Quantum optimal control functions
and
Remarkable that the interaction between nucleons at nucleus is in huge and short range. Realistic quantum control at nuclei is much more difficult and complicated than theoretic prediction. Numerous problems needs us to solve for getting definite and correct conclusion: we worry about break the particle system itself by quantum measurement, and make control nonsense. We worry whether the results what we obtained is controlled the particle; and so on. These tough issues are laying on the physics and chemistry field in the near future.
Computational approach is occurred at two spatial dimension case to fit disklike cross-section σ in nucleus as guidance. For various irregular shape cross-section, by adequate normalization or planarization, the bright idea can be extended to a broad class abstract surface inside of matter or metal. Additionally, comparison to STM image could be found from a large number of papers at atom or molecular manipulation of quantum dot.
Discussion
For control of one type particles in cost function (8), it concerns nuclear reaction, such as neutron absorption cross-seciton of uranium 235U fission to neutrons by inserting control rod for nuclear fuel. Absolutely, if require maximum of first term in criteria cost function (8), it makes emission of huge energy from chain reaction of neutrons. Cost function optimal value 5.17419 × 1023 a.u. is exactly indicating this case. Theoretical conclusion and numerical approach sufficiently verified each other, that also discriminate the uncertainties of separating or isolating simulation from realistic physics fact. It is convinced that computational result is certainly reflecting the situation of particles at a cross-section σ under proper control. Definitely, calculation of Lagrange function and Hamiltonian function H(t) for particles at a cross-section is satisfying for status of dynamical controlling. For given trajectories in spatial axes, one can define and calculate total energy potential function, Winger function as in [20] by sum of all the particles.
Concluding remark, the newly obtained results interpret and suggest that one can do control nuclear reaction at cross-section in nucleus at a substantial way. It cannot be crucial for solidly supporting by reliable particle physical concept of cross-section, developed surface science and successful quantum control theory.
Remarkably, the concept of abstract surface is breaking the subjects of definition on basic and practical surface, throughout all the scientific fields including mathematics, chemistry, physics and other areas. Beside cross-section in nucleus, abstract surface can be immediately extended and suitable to other intersecting surface. Hopefully, a completely different consideration for surface science and quantum control should be appeared. A great deal researches would be straightforwardly generated and developed by the benefit of this original work. Numerous mysteries are arising in here: quantitatively calculating the practical control force in nucleus at details; new type of physical control model; new control equipments and methodologies; new theory establishments; nuclear-scaled numerical approach; nuclear based quantum computation; and so forth. Apart from sophisticated control and traditional surface, a transparent pathway is found from surface science to nucleus. It is not just limited on quantum control, a perfect shortcut and interface to start a lot of discoveries and inventions from inside to outside. It is a confident insight along the direction to one of frontier realms.
Questions
A few questions are asked on quantum control nucleus at cross-section.
i) Why cross-section is selected for controlling particles in nuclei, not other mechanism or methodologies?
In fact, particles interacted others just like a kind of random Brown motion, or scatter. It is nonsense if tracking one particle using a laser-like force (gamma ray, γ, massless photon). As is well known, annihilation of electron-positron pair to produce fermion anti-fermion pair and Tevatron proton-proton collision to produce Higgs particles (massive scale field, neutral Higgs boson) for fitting unsymmetric electroweak field at CERN (Higgs theory [2] awarded Nobel Prize 2013). Different from moving atom or molecular using tip of STM, it is incredible using one particle to interact (or collision) to another [7], at current experimental level, LHC, one can produce a large number of particles (electron, proton) to interact or collide other large number of particles (positron, proton). It is quite like detect or discover a new particle, such as Higgs. For a tiny particle, its three-dimensional motion is not so important than that on two-dimensional cross-section. Although no awareness, indeed, it had and have being adopted on the CERN, SLAC, LHC, ALICE, etc. All detected result is intersected 2D picture of particles. In resultant, it is enough to control particle through cross-section at nucleus.
ii) How control takes place at cross-section?
Actually, aiding of the concept of cross-section, one can do control particles at nucleus directly, immediately and straightforwardly. At least, it is sufficiently for controlling particle now quantitatively, calculably in real physical lab. Theoretically, one can freely choose any cross-section for control purpose. Analytically, particles scatter to each other elastically or inelastically, using their incident angle to calculate and formulate the differential of cross-section dσ. In converting to a solvable differential equation mathematically, no problems there whatever kind of particles involving control. Not lost of generality, cross-section give us huge space to do control in nuclei scale. In practice, benefitting from mutated equipments, one can control particles just like detect them.
iii) Never use one force to control or track a particle trajectory one by one in 3D nucleus solidly?
It is completely depended on the new instruments or improved equipments. Nowadays, one can step-forward to cross-section firstly.
iv) It needs clarifying that control at cross-section just in one atom?
No, Control taking place in a atom, it is a limited theoretic case. Neutrons chain reaction indicate a amount of neutrons fission from 235U, and non-stopping collide to others. It is covered in the scope of quantum control.
Conclusions
Consequently, initially in this work, controlling of many-body problem is explored for particles at rational abstract surface of a cross-section σ in nucleus. Particle is changing from ground state to exciting state by acting of appropriate external forces. Theoretical and computational study is fairly interesting in the area of particle and quantum physics. To do control at abstract surface would be a new field of surface science in laboratory experiments aiding of modern advanced optical tools [22].
Acknowledgements
Thanks to IBM www.ibm.com/vis/stm/ for Scanning Tunneling Microscope,and Particle physics www.slac.stanford.edu. Different from traditional surface science, this work suggest a new subject named as "Abstract Surface Science" include all consideration of study on extracting cross-section, intersect surface from inside matter or metal as abstract surface, cover their generation and application. Thanks to Prof. Herschel A. Rabitz for invitation to visit Princeton University 2007. Thanks to W. Happer, A. Pechen, F. Tao, Y. Ohtsuki, S. Nakagiri, V. P. Belavkin, C. Cao, L. Techy, J. Luo, J. Kovats for useful discussion and comments.
Acknowledgments to European Science Foundation 2008, University of Connecticut Research Foundation (UCRF) and NASA/Pratt & Whitney 2007, National Natural Science Foundation of China (no. 60474027) 2004, China Postdoctoral Scientific Foundation (no. 33) 2003.

