
International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 1, Issue 1
Original Article
DOI: 10.35840/2631-5017/2501
Algebraic Collective Model Description of 166Er
G Thiamova*
Figures
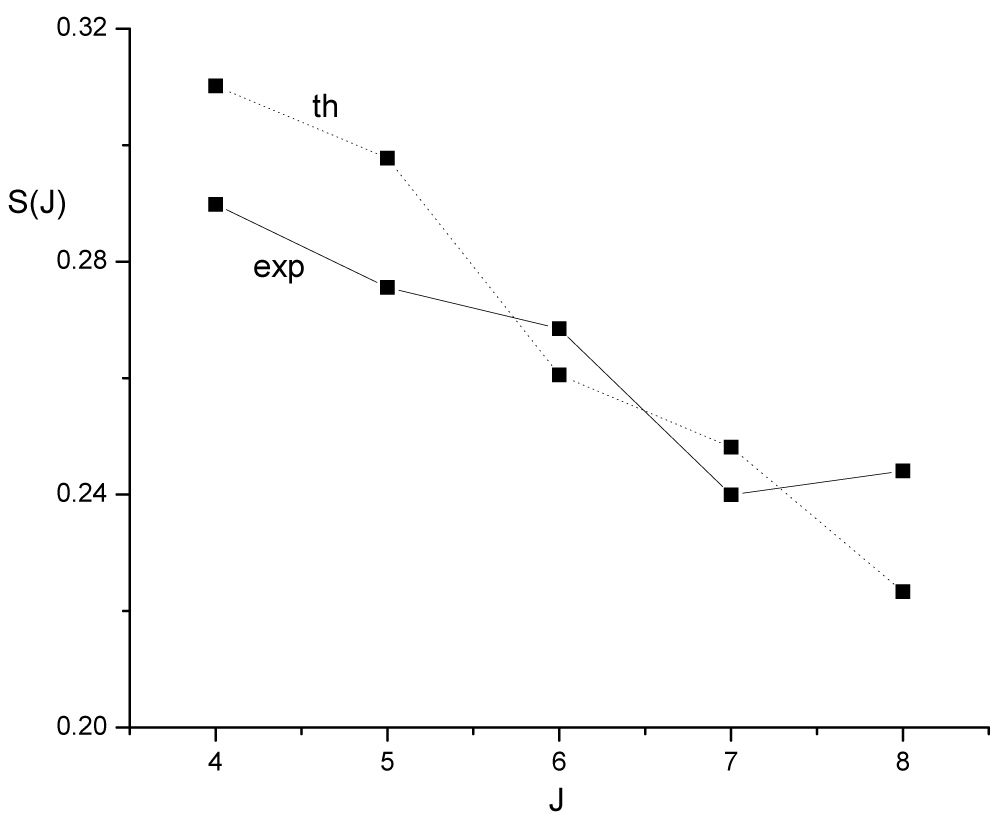
Figure 2: Experimental and calculated quasi-γ-band staggerings of 166Er.
Experimental and calculated quasi-γ-band staggerings of 166Er.
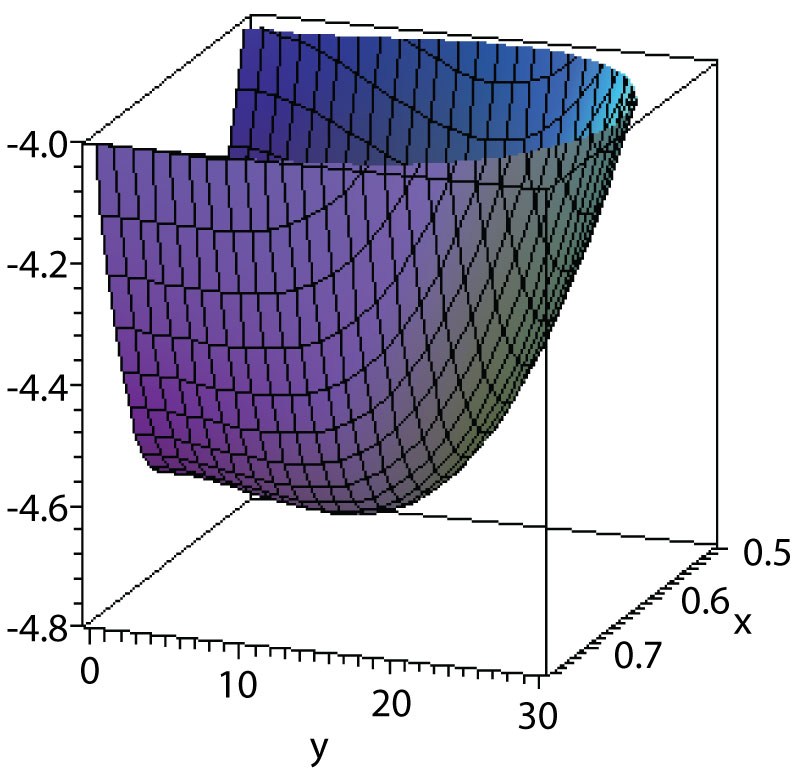
Figure 3: Potential energy surface obtained for 166Er and the Hamiltonian parameters as in Figure 1(b). Deformation parameters γ and β...
Potential energy surface obtained for 166Er and the Hamiltonian parameters as in Figure 1(b). Deformation parameters γ and β are shown on the y and x axes, respectively.
Tables
Table 1: Observed and calculated B (E2) values shown as percentages of that for the 2gs → 0gs.
References
- Bohr A, Mottelson AR (1975) Nuclear Structure. Vol. II Benjamin Reading, Massachusetts.
- Zawischa D, Speth J, Pal D (1978) Low- and high-energy collective states of deformed nuclei. Nuclear Physics A 311: 445-476.
- Garrett PE, Kadi M, McGrath CA, Sorokin V, Min Li, et al. (1997) The nature of 0+ excitations in 166Er. Physics Letters B 400: 250-254.
- Wu X, Aprahamian A, Fischer SM, Reviol W, Liu G, et al. (1994) Multiphonon vibrational states in deformed nuclei. Phys. Rev. C 49: 1837.
- Garrett PE, Kadi M, Min Li, McGrath CA, Sorokin V, et al. (1997) Kπ=0+ and 4+ Two-Phonon γ-Vibrational States in 166Er. Phys. Rev. Lett. 78: 4545.
- Borner HG, Jolie J, Robinson SJ, Krusche B, Piepenbring R, et al. (1991)Evidence for the existence of two-phonon collective excitations in deformed nuclei. Phys Rev Lett 66: 691.
- Fahlander C, Axelsson A, Heinebrodt M, Haertlein T Schwalm D (1996) Two-phonon γ-vibrational states in 166Er. Physcis Letters B 388: 475-480.
- Guessous A, Schulz N, Phillips WR, Ahmad I, Bentaleb M, et al. (1995) Harmonic Two-Phonon γ-Vibrational State in Neutron-Rich 106Mo. Phys Rev Lett 75: 2280.
- Corminboeuf F, Jolie J, Lehmann H, Fohl K, Hoyler F, et al. (1997) Kπ = 4+ double-γ vibration in 164Dy. Phys Rev C 56: R1201.
- Soloviev VG, Sushkov AV, Yu. Shirikova N(1995) Description of low-lying vibrational and two-quasiparticle states in 166Er. Phys Rev C 51: 551.
- Garcia-Ramos JE, Alonso CE, Arias JM, Van Isacker P, Vitturi A (1998) Intrinsic structure of two-phonon states in the interacting boson model. Nuclear Physics A 637: 529-546.
- Rowe DJ (2004) A computationally tractable version of the collective model. Nuclear Physics A 735: 372-392.
- Rowe DJ, Turner PS (2005) The algebraic collective model. Nuclear Physics A 753: 94-105.
- Rowe DJ (2005) An algebraic approach to problems with polynomial Hamiltonians on Euclidean spaces. Journal of Physics A: Mathematical and General 38: 47.
- Zamfir NV, Casten RF (1991) Signatures of γ softness or triaxiality in low energy nuclear spectra, Physics Letters B 260: 265-270.
- Bohr A (1952) The coupling of nuclear surface oscillations to the motion of individual nucleons, Matematisk-fysiske Meddelelser Det Kongelige Danske Videnskabernes Selskab 26: 14.
- Rowe DJ, Wood JL (2010)Fundamentals of Nuclear Models; Foundational Models World Scientific, Singapore Vol. 2.
- Hess PO, Maruhn JA, Greiner W (1981) The general collective model applied to the chains of Pt, Os and W isotopes. J Phys G: Nucl Phys 7: 737.
- Gneuss G, Greiner W (1971) Collective Potential Energy Surfaces and Nuclear Structure. Nuclear Physics A 171: 449-479.
- Caprio MA, Rowe DJ, Welsh TA (2009) Construction of SO(5) ⊃ SO(3) spherical harmonics and Clebsch-Gordan coefficients. Computer Physics Communications 180: 1150-1163.
- Welsh TA, Rove DJ (2008) A computer code for calculations in the algebraic collective model of the atomic nucleus.
- Rowe DJ, Welsh TA, Caprio MA (2009) Bohr model as an algebraic collective model. Phys Rev C 79: 054304.
- Caprio MA (2005) Effects of β-γ coupling in transitional nuclei and the validity of the approximate separation of variables. Phys Rev C 72: 054323.
- Rowe DJ (2010) Nuclear Collective Motion: Models and Theory. World Scientific, Singapore.
- Turner PS, Rowe DJ (2005) Phase transitions and quasidynamical symmetry in nuclear collective models. II. The spherical vibrator to gamma-soft rotor transition in an SO(5)-invariant Bohr model. Nuclear Physics 756: 333-355.
- Caprio MA (2011) Exact diagonalization of the Bohr Hamiltonian for rotational nuclei: Dynamical γ softness and triaxiality. Phys Rev C 83: 064309.
- Rosensteel G, Rowe DJ, (1977) Nuclear Sp(3, R) Model Phys Rev Lett 38: 10.
- Iachello F (2003) Phase Transitions in Angle Variables Phys Rev Lett 91: 132502.
- www.nndc.bnl.gov/ensdf/
- Bohr A, Mottelson BR (1982) On the Spectrum of 168Er. Physica Scripta 25: 28.
- Yoshinaga N, Akiyama Y, Arima A (1986) sdg Interacting-Boson Model Applied to 168Er. Phys Rev Lett 56: 1116.
- Yoshinaga N, Akiyama Y, Arima A (1988) sdg interacting-boson model in the SU(3) scheme and its application to 168Er. Phys Rev C 38: 419.
- Reiner AS, (1961) Electric monopole transitions in collective nuclei. Nuclear Physics 27: 115-133.
- Wood JL, Zganjar EF, de Coester C, Heyde K (1999) Electric monopole transitions from low energy excitations in nuclei. Nuclear Physics A 651: 323-368.
- Wimmer K, Bildstein V, Eppinger K, Gernhauser R, Habs, et al. (2008) D First identification of large electric monopole strength in well-deformed rare earth nuclei. arXiv: 0802.2514v1.
- G. Thiamova, M. Abolghasem (2014) Algebraic Collective Model and Nuclear Structure Applications. A Phys Pol B 45: 1833.
Author Details
G Thiamova*
Laboratoire de Physique Subatomique et de Cosmologie, Universite Joseph Fourier, France
Corresponding author
G Thiamova, Laboratoire de Physique Subatomique et de Cosmologie, IN2P3-CNRS/Universite Joseph Fourier, F-38026 Grenoble Cedex, France, E-mail: [email protected]
Accepted: September 22, 2015 | Published Online: September 26, 2015
Citation: Thiamova G (2015) Algebraic Collective Model Description of 166Er. Int J At Nucl Phys 1:001.
Copyright: © 2015 Thiamova G. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A simple, four-parameter algebraic collective model (ACM) Hamiltonian is used to describe 166Er. In this nucleus anharmonic double-γ vibrations are observed and the third excited 0+ state has been identified as a candidate for a bandhead of a β band. In contrast to γ-vibrational bands, systematically observed in deformed nuclei, β-vibrational bands are rarely well realized in nuclei and their observation and interpretation is still far from satisfactory. The purpose of the present paper is to show how the ACM model is capable to address complex properties of deformed nuclei in this region and what are its successes and weak points.
PACS
21.60Ev, 21.60FW
Introduction
Nuclear quadrupole shape oscillations are traditionally described as β and γ vibrations [1]. The β vibrations preserve axial symmetry and a one-quantum excitations give rise to K = 0+ bands where K is the projection of the angular momentum on the symmetry axis of the nucleus. A γ vibration dynamically breaks the axial symmetry and leads to K = 2+ bands. γ-vibrational bands are systematically observed in deformed nuclei and their properties are relatively well understood. Excited 0+ states, on the other hand, provide some of the greatest challenge to nuclear structure models and their interpretation remains still very unsatisfactory.
For many years, the O+2 excited state has been interpreted as a β vibration [1]. However, as more data become available it has been realized that those states do not have enhanced B(E2) transitions to the states as should be expected for a β vibration. Based on the two-neutron transfer experiments, it has been suggested that many low-lying 0+ states were pairing-type excitations [2]. In order to give guidelines as to how a β vibration should behave one may rely on the microscopic liquid drop model predictions [1]. One would find that the β vibration should have values of about 10 W.u., i.e. comparable to those of the γ vibration.
In 166Er lifetimes of excited 0+ states have been measured with the (n, n'γ) reaction [3]. The first and second excited 0+ states have been shown to have no significant collective enhancement of their decays to the ground band and their properties are suggestive of pairing-type excitations rather than those of a β vibration. The third excited 0+ state at 1934 keV, on the other hand, has an enhanced decay to the ground band with = 8.8 W.u., consistent with what is expected for a β vibration.
The existence of two-phonon states in deformed nuclei has also been the subject of considerable debate over decades. Following the discovery of the state in 168Er [4] attempts were made to locate these states in other nuclei, mainly by considering branching ratios and energy systematics. In 166Er levels at 1943 keV and 2028 keV have been observed with collective transitions to the γ band. The former, state, has thus been identified as a K = 0+ double-γ vibration [5] and the latter has been interpreted as a K = 4+ double-γ vibration. Interestingly, a large range of anharmonicities of these double-γ vibrations is observed [6-9]. These states and their anharmonicities are of a great interest since they provide a stringent test of nuclear models. For example, the Quasiphonon Nuclear Model predicts no K = 0+ double-γ vibrations below 2.5 MeV in 166Er [10]. A study of double-γ vibrations using the intrinsic-state formalism of the Interacting Boson Model (IBM) has revealed that large anharmonicities can only be obtained for a finite number of bosons combined with a three-body term in the Hamiltonian that can induce triaxiality [11]. However, in such a description, problems arise for the moments of inertia, in particular for the γ bands.
From the above it is clear that the description of the structure of 166Er presents a real challenge for nuclear models. The purpose of the present analysis is to identify the limitations of the algebraic collective model (ACM) [12-14] as much as its successes in such a kind of description. An emphasis is placed on a good description of the excitation energies and relative positions of ground bands and excited β and γ bands. An attention is also payed to the description of the quasi-γ band staggering that has been found to represent a useful signature of γ softness or rigid triaxiality in low-energy and low-spin nuclear spectra [15]. Parameters of the Hamiltonian obtained from the fit of the energy spectrum are then used to analyse electromagnetic transition rates which are found to be in a reasonable agreement with the experimental data.
The ACM is briefly explained in the next section. In third section the calculations are presented and compared to the data. In the last section we raise some important questions that would deserve further investigation.
ACM model calculations
The ACM, introduced as a computationally tractable version of the Bohr model (BM) [16] restricted to rotational and quadrupole vibrational degrees of freedom, is characterized by a well defined algebraic structure [see ref. [17] for a review of this model]. Unlike the conventional U(5) ⊃ SO(5) ⊃ SO(3) dynamical subgroup chain used, for example, in the Frankfurt program [18,19], the ACM makes use of the subgroup chain
to define basis wave functions as products of β wave functions and SO(5) spherical harmonics. Several advantages result from this choice of dynamical subgroup chain: (i) with the now available SO(5) Clebsch-Gordan coefficients [20,21], and explicit expressions for SO(5) reduced matrix elements, matrix elements of BM operators can be calculated analytically; (ii) by appropriate choices of SU(1,1) modified oscillator representations, the β basis wave functions range from those of the U(5) ⊃ SO(5) harmonic vibrational model to those of the rigid-beta wave function of the SO(5)-invariant Wilets-Jean model; and (iii) with these SU(1,1) representations, collective model calculations converge an order of magnitude more rapidly for deformed nuclei than in U(5) ⊃ SO(5) bases. Thus, the ACM combines the advantages of the BM and the IBM and makes collective model calculations a simple routine procedure [12,13,22,23].
In the ACM, fully converged calculations were performed in Ref. [22] for a range of Hamiltonians to determine the extent to which experimental data can be realistically described in terms of the BM. More importantly, they prepare the way for more general, but still solvable, algebraic collective models that include intrinsic degrees of freedom as in the unified model of Bohr and Mottelson [1,24-27].
An essentially unlimited variety of combined β and γ dependencies (e.g. βmcosn3γ) can be used in the ACM potential. For physical reasons, one would normally restrict consideration to Hamiltonians that are time-reversal and rotationally (i.e. SO(3)) invariant. As an example, the potential V (β, cos3γ) may be a polynomial in β2 or βcos3γ. However, even terms such as β and cos3γ, that are irrational functions of the coordinates, can be easily computed numerically. An important concern is the extent to which one can construct collective model potentials for the ACM that have minima at arbitrary values of β0 and γ0 and corresponding arbitrary rigidity parameters. One such a general purpose ACM Hamiltonian is given, for example, in the form
where
is the Laplacian on the 5-dimensional collective model space [17]. An advantage of such a parametrization is that various limits of the BM correspond to simple parameter sets, identified in Ref. [22].
The above Hamiltonian, expressed in terms of the quadrupole deformation parameters β and γ serves as a useful starting point for a description of a wide range of nuclear collective spectra. Moreover, it has been shown, that this kind of Hamiltonian can be exploited in the study of a phase transition between axial and triaxial deformations [28] or in the study of the second-order phase transition of a model nucleus, from a spherical to a deformed phase, with α as a control parameter [25]. For α = 0 the potential is that of a spherical harmonic oscillator, , while for α > 0.5 it has a minimum for a non-zero value of β, which increases as α increases. Moreover, as the mass parameter M of the Hamiltonian (2) increases, the kinetic energy decreases and the result is a decrease of the vibrational β fluctuations of the model about its equilibrium deformation. Thus, the value of the parameter α controls the β deformation of the model and the parameter M controls its rigidity. By adjusting the parameters α and M a model with any equilibrium value of the β deformation and any degree of rigidity may be constructed. In Ref. [22] it has been shown that parameter values in the range 0 < α < 2.0 and 10 < M < 100 are sufficient to describe the β deformations and rigidities of the observed nuclear collective states.
The terms β2 and cos3γ in eq. (2) are defined in terms of the quadrupole tensor operator by
It is because of the presence of the last term proportional to cos23γ that a triaxial minimum in the potential energy surface (PES) may appear. A delicate competition between all the three terms in the potential and the second and the third one in particular will determine whether the potential energy minimum will remain axially symmetric (second term proportional to cos3γ dominates) or will be driven to a triaxial minimum by the last term.
It should be noted that the prolate to oblate transition is obtained trivially by changing the sign of the parameter χ and this sign change does not produce any effect on the calculated spectra as the Hamiltonian (2) is isospectral with regard to this sign transformation.
In order to minimize a deviation of the experimental and calculated energy values a least-square method has been used in a suitable part of the multidimensional parameter space defined above. The procedure was carried out in two steps. First coarse-grain fits were performed to narrow down the parameter space to a physically meaningful subspace. In the second step fine-grain fits were done with steps ΔM = 0.5, Δα = 0.1, Δχ = 0.1 and Δκ = 0.1 to obtain final results. All the experimental levels (shown in Figure 1a) were included in the fit characterized by a value of χ2 = 139.
Results
In this section results obtained with the ACM Hamiltonian (2) are presented. First in Figure 1(a,b) the calculated energy spectra are compared with the available experimental data taken from Ref. [29]. The parameters, used in the calculation, are shown in Figure 1(b). In general, the calculation provides a reasonable description of the ground and first excited band. What are the predictions of the ACM with regards to two-phonon states and their large anharmonicities? We observe that the calculated energies of the two-phonon states fall below those observed and thus the calculated anharmonicities of those states are much smaller than the experimental ones. One could easily show that by increasing, for example, the parameter κ of the last term in the Hamiltonian (2), that drives the system towards a triaxial minimum, would substantially increase the anharmonicities. However, the moments of inertia of the γ bands, and the band in particular, would be strongly perturbed.
The study of anharmonicities in nuclear spetra has a long history. Within the IBM-1, it has been shown some time ago by Bohr and Mottelson [30] that large anharmonicities, as observed for instance in 166Er, cannot be described. Subsequently, it was shown that one would need a g boson with l = 4 in addition to the s and d bosons [31,32]. More recently, a study of two-phonon states in the IBM-1 was reported [11] which showed that the IBM-1 is a harmonic model in the limit of large boson number. Anharmonicities can only exist for finite boson number but they are small if only two-body interactions are used. It was also suggested that anharmonicities are strongly linked to triaxiality, which can be induced by three-body terms in the potential. The ACM, even if capable of giving rise to a stable triaxial minimum does not satisfy the condition of a finite boson number to be able to accommodate large anharmonicities. It could only do so by increasing the triaxiality artificially so that the position of the bands and their moments of inertia would be substantially perturbed.
It is also notable that the spectrum is quite β rigid which is reflected by a large value of the mass parameter M. In fact, many nuclear spectra are much more β rigid than one would expect, a fact, that can be linked to the absence of large centrifugal stretching effects. From the perspective of the ACM, a large amount of centrifugal stretching would otherwise result and would be observed, e.g. in the ground-state rotational band energies which would systematically fall below the experimental ones. As a consequence of this substantial β rigidity many β vibrational bands appear in the higher-energy domain.
It should be noted that to identify a potential candidate for a β vibration B(E0) transition rates may be used [33]. Wood et al. [34] has given a detailed account of both experimental and theoretical B(E0) properties. They have pointed out that the β vibration should give rise to enhanced B(E0) transitions to the ground state due to the radial shape oscillations in β. In case of 166Er, the large electric monopole strength clearly identifies the state at 1934 keV to be the β vibrational excitation of the ground state (see [35]) and it would be interesting to compare it with the ACM prediction once the calculation of the B(E0) transition rates is implemented in the code.
The B(E2) transition rates are shown in Table 1. The strengths of the intraband B(E2) transition rates are in a reasonable agreement with the experimental ones. A small effect of the centrifugal stretching is nevertheless reflected by B(E2) values for higher spin states that exceed the observed ones. The strengths of the interband B(E2) transition rates are fairly described. However, the calculated B(E2) transition rate for the 0β → 2γ transition is non-zero and quite large which suggests a strong band mixing of the calculated states. As for the K = 4+ double-γ vibration, no transition to the ground-state band has been observed, a results which is in agreement with its double-phonon interpretation. The calculation also predicts this transition to be zero.
Analysis of the experimental staggering in different isotopic chains has revealed different patterns that can be categorized based on the standard limits known in, for example, the IBM based models. One example are nuclei that represent the transition between vibrational and γ-soft structures that show strong staggering with negative S(J) values at even-J and positive S(J) values at odd-J spins. The heavy rare-earth nuclei known to display an axially symmetric behavior show a similar staggering pattern with a smaller overall magnitude. On the other hand, triaxial nuclei display a staggering pattern with positive S(J) values at even-J and negative S(J) values at odd-J spins. It can be expected that when going from axially symmetric to triaxial nuclei the staggering amplitude would decrease step by step and would eventually flip into the pattern characteristic of triaxial nuclei. The triaxial staggering amplitude should then increase with increasing β rigidity of the potential [36]. However, irregularities of the staggering pattern may be expected for nuclei in the transition region. For example, an irregular pattern is observed for 188Os while the staggering pattern of 192Os is characteristic of a soft triaxial rotor with positive S(J) values at even-J and negative S(J) values at odd-J spins, with a small positive values S(4) corresponding to a soft potential in the γ direction. In case of 166Er, an irregular pattern is observed, whose general behavior is more or less reproduced by the calculation even if the absolute values of S(J) are less correctly described. Interestingly, the corresponding PES, shown in Figure 3, reveals existence of a very shallow triaxial minimum. Irregularities of the quasi-γ band staggering should be systematically investigated to see what kind of information they provide about shape changes in nuclei.
Discussion
The ACM enables one to carry out easy collective model calculations for a diverse range of Hamiltonians and for essentially arbitrary values of β and γ stiffness. A primary objective of analyzing data within a model is to identify the model's deficiencies and suggest ways in which it could be improved. Obviously, this goal can only be achieved when many experimental spectra for various ACM Hamiltonians are analysed. This paper represents an attempt in this direction.
The ACM can account for a wide variety of γ-vibrational anharmonicities in nuclei such as those observed in 166Er but not without substantially changing the moments of inertia and energy positions of various bands. The knowledge of the two double-γ-vibrational bands (with K = 0+ and K = 4+ provides a stringent test of nuclear models and, in particular, of the type and strength of three-body interactions [11]. From the theoretical perspective, all types of three-body interactions should be tested against experimental data.
The behavior of quasi-γ band staggering seems to be quite complex in realistic cases. A question arises as how to systematize in more detail their behavior including nuclei that represent a transition between different shapes and how to understand irregularities that appear in the behavior of S(J) as a function of structural changes, β and γ stiffness, relative positions of β and γ bands etc. Those questions should be investigated systematically from the experimental and theoretical standpoint.


