International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 4, Issue 1
Research Article
DOI: 10.35840/2631-5009/7523
Haptic Assisted Virtual Tele-Operation of Robotic Manipulator for Smooth Space Debris Capturing
Mutian Li* and Xiutian Yan
Table of Content
- Abstract
- Introduction
- Literature Review
- Reaction Control Solution
- Velocity Control with Haptic Guidance
- Capturing Methods with Haptic Guidance
- Experiment Setup
- Results, Findings and Discussion
- With Dynamic Guidance
- With Artificial Potential Field (APF) Method
- Discussion of the Graphic Results
- Discussion of Quantitative Results
- Objective Performance
- Limitation and Future work
- Conclusion
Figures

Figure 3: The haptic device used in this...
The haptic device used in this experiment, Geomagic Touch X and its workspace frame.
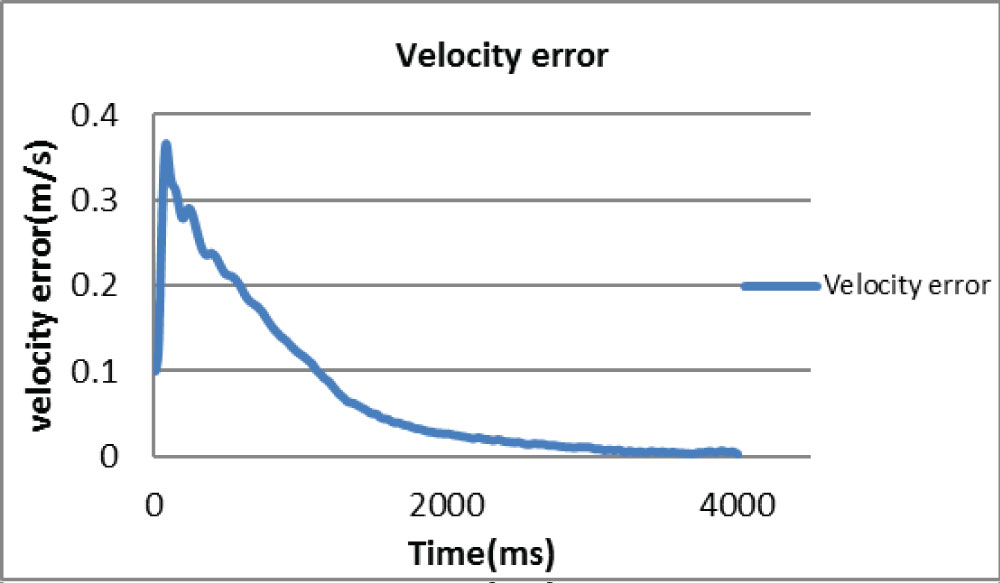
Figure 5: Velocity error between the end...
Velocity error between the end effector and the target with dynamic guidance.

Figure 6: Position error between the end...
Position error between the end effector and the target with dynamic guidance.
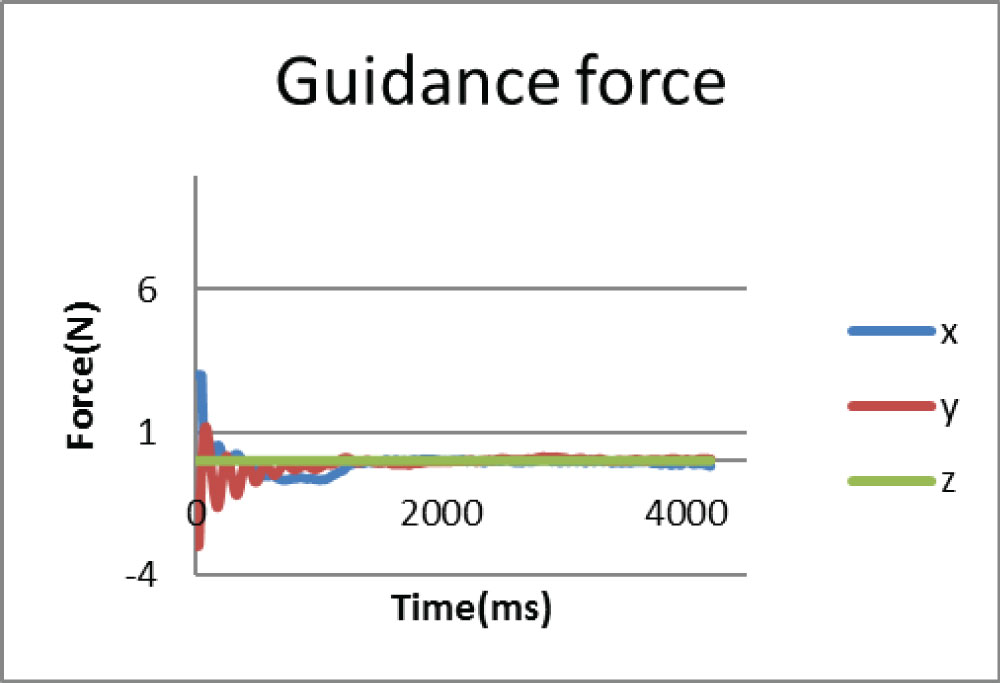
Figure 10: Actuated guidance force after rendering...
Actuated guidance force after rendering for dynamic guidance methods.
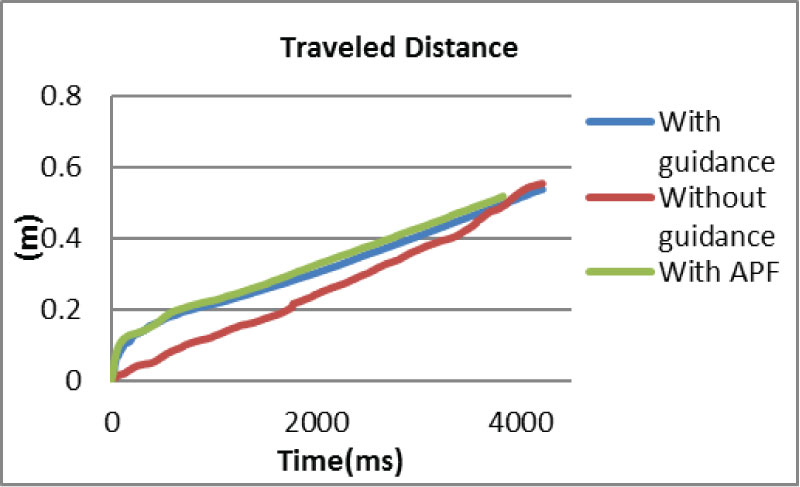
Figure 13: Comparison of travelled distance...
Comparison of travelled distance until reaching the target.
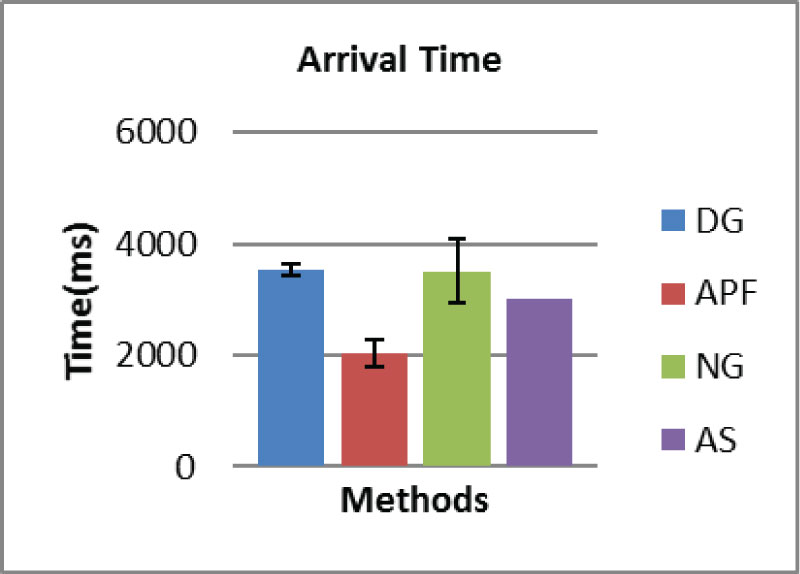
Figure 16: The means of times used to reach the...
The means of times used to reach the target at first time (when the distance = 0), with shown standard derivation.
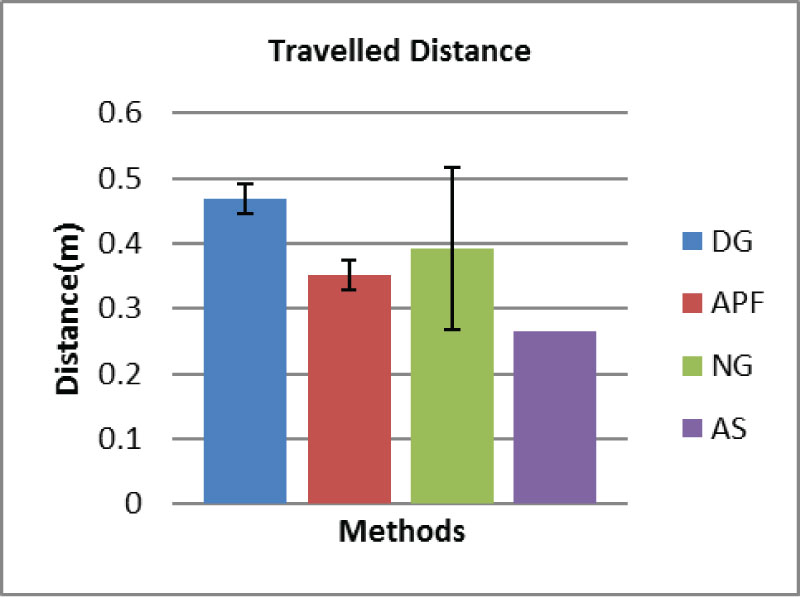
Figure 17: The means of travelled distances before...
The means of travelled distances before reaching the target with shown standard derivation.
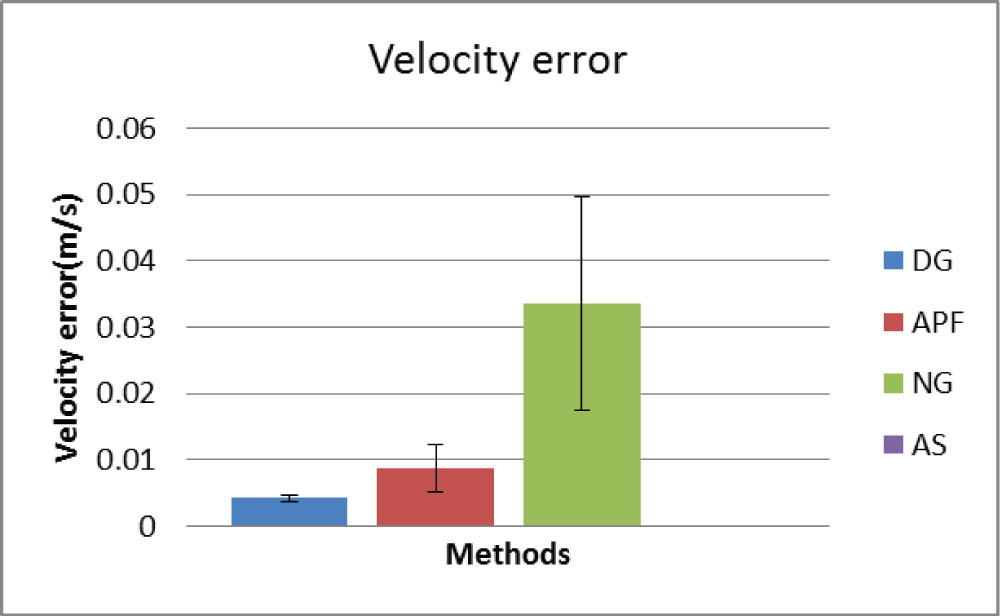
Figure 18: The means of velocity errors at the...
The means of velocity errors at the point of first reaching the target with shown standard derivation.

Figure 19: The MSE (mean squared error) of the...
The MSE (mean squared error) of the relative velocity and position in 1000 ms after reaching the target space debris.
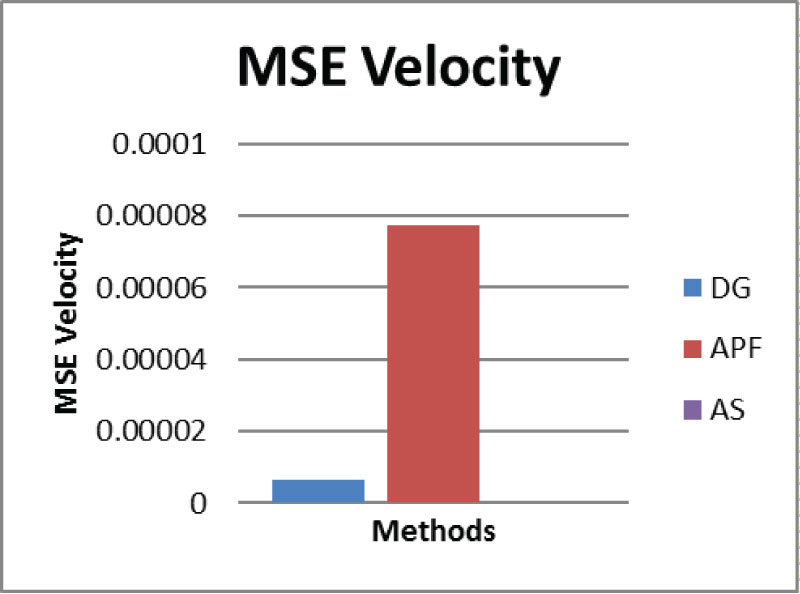
Figure 20: The MSE (mean squared error) of the...
The MSE (mean squared error) of the relative velocity in 1000 ms after reaching the target.

Figure 21: The MSE (mean squared error) of the relative...
The MSE (mean squared error) of the relative position in 1000 ms after reaching the target.
References
- RE Lindberg, RW Longman, MF Zedd (1990) Kinematic and dynamic properties of an elbow manipulator mounted on a satellite. Journal of the Astronautical Sciences 38: 397-421.
- S Dubowsky, MA Torres (1991) Path planning for space manipulators to minimize spacecraft attitude disturbances. IEEE International Conference on Robotics and Automation 1-3: 2522-2528.
- JJ Abbott, P Marayong, AM Okamura (2007) Haptic virtual fixtures for robot-assisted manipulation. Robotics Research Proceedings Paper 28: 49.
- S Dubowsky, E Papadopoulos (1993) The kinematics, dynamics, and control of free-flying and free-floating space robotic systems. IEEE Transactions on Robotics and Automation 9: 531-543.
- D Nenchev, Y Umetani, K Yoshida (1992) Analysis of a redundant free-flying spacecraft manipulator system. IEEE Transactions on Robotics and Automation 8: 1-6.
- F Caccavale, B Siciliano (2001) Kinematic control of redundant free-floating robotic systems. Advanced Robotics 15: 429-448.
- S Cocuzza, I Pretto, S Debei (2012) Least-squares-based reaction control of space manipulators. Journal of Guidance Control and Dynamics 35: 976-986.
- YN Zhang, J Wang, YS Xia (2003) A dual neural network for redundancy resolution of kinematically redundant manipulators subject to joint limits and joint velocity limits. IEEE Transactions on Neural Networks 14: 658-667.
- KA O'Neil (2002) Divergence of linear acceleration-based redundancy resolution schemes. IEEE Transactions on Robotics and Automation 18: 625-631.
- S Cocuzza, M Li, X Yan (2016) Soft and minimum reactions robotic capture of non-cooperative spacecrafts. In: 67th International Astronautical Congress 2016, 3748.
- LB Rosenberg (1993) Virtual fixtures - perceptual tools for telerobotic manipulation. Ieee Virtual Reality Annual International Symposium 76-82.
- B Kuang, S Payandeh, B Zheng, F Henigman, CL MacKenzie (2004) Assembling virtual fixtures for guidance in training environments. 12th International Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems 367-374.
- S Payandeh, Z Stanisic (2002) On application of virtual fixtures as an aid for telemanipulation and training. 10th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Proceedings, Proceedings Paper 18-23.
- SA Bowyer, BL Davies, FRY Baena (2014) Active constraints/virtual fixtures: A survey. IEEE Transactions on Robotics 30: 138-157.
- N Turro, O Khatib, E Coste-Maniere (2001) Haptically augmented teleoperation. In IEEE International Conference on Robotics and Automation 386-392.
- Mario Selvaggio, Fei Chen, Boyang Gao, Gennaro Notomista, Francesco Trapani, et al. (2016) Vision based virtual fixture generation for teleoperated robotic manipulation. 2016 International Conference on Advanced Robotics and Mechatronics (ICARM) 190-195.
- XJ He, YH Chen (2008) Six-degree-of-freedom haptic rendering in virtual teleoperation. Ieee Transactions on Instrumentation and Measurement 57: 1866-1875.
- J Artigas, G Hirzinger (2016) A brief history of DLR's space telerobotics and force-feedback teleoperation. Acta Polytechnica Hungarica 13: 239-249.
- J Artigas, Balachandran Ribin, De Stefano Marco, Panzirsch Michael, Lampariello Roberto, et al. (2016) Teleoperation for on-orbit servicing missions through the ASTRA geostationary satellite. In IEEE Aerospace Conference, New York.
- Y Umetani, K Yoshida (1989) Resolved motion rate control of space manipulators with generalized jacobian matrix. Ieee Transactions on Robotics and Automation 5: 303-314.
- S Cocuzza, I Pretto, C Menon, F Angrilli (2007) Control of dynamic attitude disturbances on spacecrafts equipped with robotic systems for orbital maintenance. Presented at the 58th International Astronautical Congress 2007.
- S Cocuzza, I Pretto, F Angrilli (2008) Optimal kinematic control of redundant space robotic systems for orbital maintenance: Simulated microgravity tests. In: 59th International Astronautical Congress 2008 1: 601-614.
- AC Forsyth, KE MacLean (2006) Predictive haptic guidance: Intelligent user assistance for the control of dynamic tasks. IEEE Transactions on Visualization and Computer Graphics 12: 103-113.
Author Details
Mutian Li* and Xiutian Yan
Department of Design, Manufacture and Engineering Management, Space Mechatronic Systems Technology Laboratory, University of Strathclyde, UK
Corresponding author
Mutina Li, Department of Design, Manufacture and Engineering Management, Space Mechatronic Systems Technology Laboratory, University of Strathclyde, Glasgow, UK.
Accepted: February 04, 2019 | Published Online: February 06, 2019
Citation: Li M, Yan X (2019) Haptic Assisted Virtual Tele-Operation of Robotic Manipulator for Smooth Space Debris Capturing. Int J Astronaut Aeronautical Eng 4:023.
Copyright: © 2019 Li M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
There are a number of challenges in space exploration missions and a growing challenge is the economic and efficient removal of space debris. A number of methods have been studied in literature to remove space debris which increase rapidly. This paper presents a novel method for capturing a targeted space debris in space using a robot with redundant degrees of freedom enabled with the assistance of haptic guidance. The proposed method features transferring a null reaction torque to the base spacecraft during the operation. The robot and the end-effector is controlled and manipulated by an operator with the assistance of a haptic guidance based controller that makes the position and velocity errors converge to zero before reaching the target at a desired velocity. The proposed method is demonstrated by means of dynamic and graphic simulations using a haptic interface to drive the robot. These simulations have shown a satisfactory performance in capturing the target space debris by showing a spacecraft can be maintained stable as null reaction torque is transferred during the rendezvous and interaction between the robot and the space debris. The haptic guidance method implemented in a dynamic controller enabled an operator to perform planned tasks, whilst it still allowed a full control of the robotic manipulator by the human operator. This shows great advantages comparing to the current approaches for capturing target, where haptic assistance is not introduced or the path control is not dynamic.
Introduction
Space exploration has always been an ultimate dream of human beings and at the same time it is full of risks [1], hence requiring either tele-operations or full autonomous operations in situations where it is too difficult for a human being to undertake a direct manipulation task [2]. Such typical operations involve the use of space robotics whose applications could include moving equipment around space station, providing service and maintenance to the instruments and payloads of a spacecraft. The teleoperation of a space robot is an example of applications where haptic Human-Machine interactive system shows great advantages. The system can provide higher levels of precision and accuracy than those of human operators, while still allowing human operator's intelligence in decision making and reaction in the control loop to deal with complex situations in space environments with the help of haptic force feedback [3]. Some of the space manipulation tasks require capture of approaching targets, such as refuelling and maintenance of the satellites, and capturing payload or space debris. To achieve a successful object capturing, a key issue is to minimize the impacting force between the robot and the object. This requires the end-effector of the robot reaches the same position and velocity of the target at the time of capturing. Otherwise, it could cause damage to the robotic system or the target object, push away the target.
In these working scenarios, one of the most important issues is to reduce the disturbance to the base while moving the manipulator. Although the position and attitude of the spacecraft can be controlled by the reaction jets, reduced reactions to the base can result in higher energy efficiency and longer working life [4].
Literature Review
A method to analyse the redundant robotic system in free flying mode is presented [5]. The analysis is based on fundamental momentum conservation laws, and inverse kinematics is considered in order to make the end-effector follow a predefined path. In 2001 a closed-loop IK algorithms for redundant free floating manipulator is presented [6]. Generalized Jacobian is used to solve closed-loop IK for task of space robotic system. Recently an IK solution based on Least Squares to locally minimize the reaction from redundant manipulators to the spacecraft is proposed [7]. This IK solution can take the physical and mechanical constraints of the robot, in terms of joints angel, velocity and acceleration, into the algorithm of solution directly [7,8], while it also might be possible to avoid the algorithm instabilities [9].
A study of non-collaborative target capturing is presented [10]. Two novel methods for capturing target with a redundant robot are proposed and compared. Null reaction torque is ensured to transfer to the spacecraft base. This results in an advantage comparing to the other state of the art in capture methods, in which the capture and reaction minimization problems are separately handled and the integration of them isn't straightforward.
To integrate haptic in the manipulating tasks, a more specific term 'Virtual Fixture' was introduce [11]. The virtual fixture is defined as position and force signals generated by software applying on human user to improve safety and accuracy in robotic manipulating tasks [3]. According to the usages of virtual fixture, it then can be classified into two types: The guidance virtual fixture [12], and forbidden region virtual fixture [13]. As the names suggest, the guidance virtual fixture help user follow a planned path, while forbidden region virtual fixture keeps user out of a strictly constrained area. This classification is later updated to the term 'regional and guidance' active constraints by a survey in virtual fixtures [14]. The guidance active constraints, or guidance virtual fixture, may include two more specific terms: The attractive and repulsive active constraints. The attractive active constraints drive the user towards the constraints, while repulsive active constraints drive user away from the constraints.
Turro was one of early researchers who apply the virtual fixture in robotic manipulation [15]. He assigned the virtual constraints to specific robotic geometry constraints, such as robot's joints limits, workspace limits and singularities. Constrained movement such as following a curve or surface is also implemented with potential field. A vision based virtual fixtures generating system for robotic teleoperation was presented by Selvaggio [16]. Stereo cameras are used to provide accurate environment information which is essential to build the potential fields. A Six- Degrees of Freedom (DoF) Haptic Rendering for teleoperation is introduced by He and Chen [17]. The six joints of a virtual robot are mapped and coupled to a Six-DoF haptic device, rather than Three-DoF. Path following tasks are also accomplished with virtual constraints. However, the path following control in these researches is not dynamic. These virtual fixtures can only guide the user following the desired path, constrained by position but not by velocity, meaning that it's not adequate for manipulation tasks that require control of velocity during the path such as object capturing. There are researches from German Aerospace Centre investigating the bilateral control of robotic system for on-orbit servicing [18,19]. In the experiment robotic system is set to free floating mode for simulation in space environment. The force feedback is utilized to achieve delicate bilateral control of the slave robot. However, other haptic virtual fixtures such as constraints or guidance are not considered in these teleoperation tasks.
In this paper, a novel method for capturing a target in space using a robot with redundant degrees of freedom enabled with the assistance of haptic guidance is proposed. The proposed method is then demonstrated by means of dynamic and graphic simulations using a haptic interface to drive the robot.
Reaction Control Solution
For redundant space manipulator, the Forward Kinematics equation can be described as:
Where J, are the Generalized Jacobian Matrix and its time derivative of the manipulator, are the joint velocities and accelerations, and represents the desired acceleration of the end-effector [20].
And the reaction torque about the spacecraft centre of mass can be described as:
With the mass matrix M and the centrifugal and Coriolis term n.
If a desired acceleration of the end-effector, , is given, q and at present are known, Eq. 1 can be solved by the pseudoinverse of the Generalized Jacobian Matrix (Least Square Solution):
The term represents the classical pseudoinverse solution, which is the particular solution that minimizes , while the term represents the general solution of the homogeneous system , where I is the identity matrix [21].
And the base reaction torque can be represented by the quadratic cost function:
Which depends on only. Then this local constrained optimization problem can be defined as:
Min
Subject to
Where represents the local optimization variable of the joint accelerations.
A closed-form Least Squares problem with Equality constraints (LSE) [22] solution can be found for the LSE problem by combining Eqs. (2) and (3) [10]:
The solution introduced in this section will be implemented in the dynamic simulation for inverse kinematic solution in space capturing tasks in this study. The solved joints angle will then be updated in the geometric model in haptic. As a result while user moves the position of haptic device, the end effector of virtual manipulator will follow the user's command while considering reaction control. In the way the dynamic motion of the space robotic manipulator can be controlled by user with haptic device with minimization of the base reaction torque.
Velocity Control with Haptic Guidance
Methods using virtual fixtures such as potential field and constraints can achieve position control of the manipulator, guide user reach a target and avoid the obstacles. However, it doesn't control the velocity of the manipulator, which is not adequate for manipulation tasks that require control of velocity during the path such as object capturing. Therefore, the guidance force should also be introduced to assist the dynamic control of the manipulator.
The goal of haptic guidance in dynamic control of the manipulator is to reach both the desired position and velocity. Guidance force will be provided on the haptic device as assist to the user. If the user agrees with the guidance and just follows the device without applying any external forces, the end effector will reach a static or moving target position on a desired velocity. This dynamic control can be used in telemanipulation tasks such as capturing a target object with known velocity and trajectory. The guidance should produce an optimum capturing path reaching the target calculated in real time considering the travel time and distance. The user can engage and take in charge of control at any time if a better solution is available, or to deal with unexpected events such as unknown obstacles. After the engagement of user, the optimum path will be calculated again and the guidance force will be updated to continue assistance in the task. Both of these guidance methods provided for dynamic control are suggestive, still allowing full control of manipulator by the user.
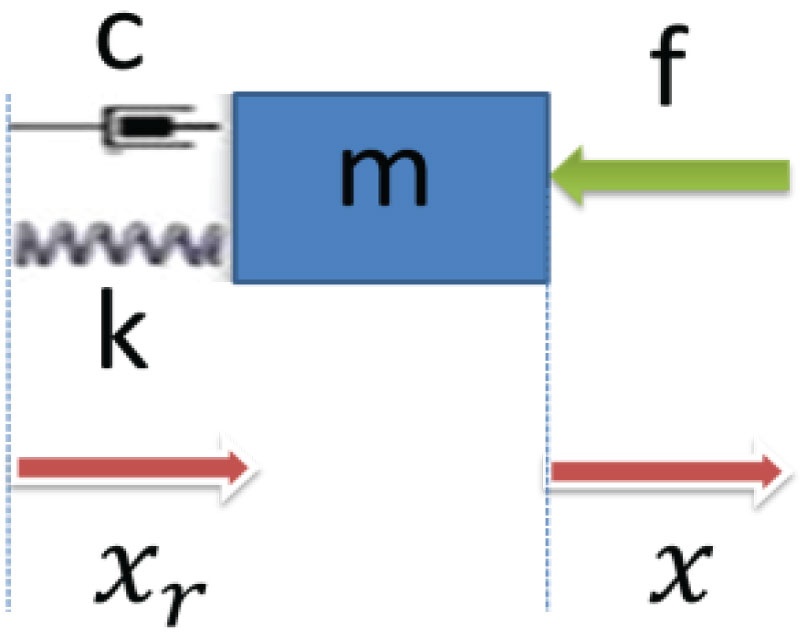
The haptic device used in this study, Geomagic Touch X, is impedance. Thus to achieve the velocity control into the haptic system, the impedance control of the haptic controller needs to be studied and implemented. Impedance control takes forces from the environment and outputs changes in positions. A typical impedance control is a linear second-order system expression with mass, spring, and damper shown in Figure 1,
Then the system fits the equation
Where , and x are acceleration, velocity and position of the end effector, m is the mass, c is the damper constant and k is the stiffness of spring. F is the external force applied on the device in the environment.
This impedance control model can be modified for the velocity control in this study. The stiffness k in the system shows the stiffness reacting to the external force applied on the device. In this case while user engages the control of manipulator, the haptic device will follow the user's command to achieve force control. So the stiffness k = 0 is set in this case model. Including the guidance force into the system, therefore the model in velocity control can be described in Figure 2:
And the system fits the equation
Where m is the mass, c is the damper constant, , are acceleration and velocity of the end effector of the device. fd is the force applied by the actuator of the device and fe is the environmental force applied by environment i.e. by the user.
So while being followed by user without any interference external force, the guidance force provided to the user should be:
Where , are acceleration and velocity error between the desired and actual values.
In this way the guidance force for velocity control is completed and can be actuated on the haptic device. For dynamic control of a desired velocity and position/path, the guidance force will be solved in the next section along with the dynamic analysis of the space manipulator.
Capturing Methods with Haptic Guidance
The next step is to introduce the haptic guidance into the system for dynamic control together with the developed capture methods described. A "Free-shape-trajectory reactionless capture method" is developed and proposed [10]. LSE method is used, the end-effector trajectory is computed by double integration of the , where the position error e and velocity error are reduced to zero by means of two gains kp and kd, such that:
Where d is the desired end-effector acceleration, and is the current end-effector acceleration.
The impedance control of haptic device developed earlier, only take into account of the velocity and acceleration in the equation.
Combining these two control method will add the position error into account which will also reduce the position error to achieve capturing task with impedance control of the haptic and reaction control of the manipulator.
In this way the capturing method is integrated into the impedance control of haptic device and can provide a guidance force to assist user reaching the desired position and velocity. Therefore it can achieve dynamic control in target capturing tasks in space environment. The performance of the control and capturing method in the system can be recorded and evaluated.
Experiment Setup
A set of experiments have been undertaken to assess the haptic feedback provided by the haptic system. The experimental environment was established in our robotics lab. The haptic device used in this experiment is the Geomagic Touch X as shown in Figure 3. It is operated by the user on a desk. The user is recruited in our Space Mechatronic Lab who has experience with both robotic control and the use of haptic device. A monitor on the desk shows the graphic model during the manipulation. The experiment procedure is shown in the Table 1. For space capturing task, three simulated teleoperation procedures are conducted. The first procedure is conducted with dynamic haptic guidance, while the second procedure is set without haptic guidance for comparison. For the third procedure, an additional experiment providing a guidance using an artificial potential field method is conducted to capture the moving target [23]. The user should at least have basic experience with the use of a haptic device. The performance of graphic and force models and the efficiency of the haptic guidance are evaluated by the user.
Results, Findings and Discussion
The capturing task requires participant to control the manipulator to reach both the desired position and velocity. This capturing task is conducted with and without the guidance force. The initial conditions of the robotic manipulator and target are again set identically as in the Matlab simulations [10], and as shown in Figure 4. The target is approaching along the x axis, and the velocity is set to 0.1 m/s. The desired operation is to ensure the end effector moves at the same velocity while reaching the target to allow smooth capture. With the guidance model, the force is provided to achieve impedance control of the end effector of the manipulator. The guidance force is provided as introduced earlier, with kp = 7.7 and kd = 5 in this study:
These factors are decided as a result of sensitivity analysis conducted in an earlier study that proved to always be able to reach the target at desired speed and directions in given tasks [10].
To be noted here is that a 0.0044 m is deducted from the original distance between the coordination of the end effector and the target as it's the radius of the target object in the calculation of the distance. It means when the end effector touches the surface of the target it can be regarded as "reaching" the target. Therefore the distance data in the following results can be slightly below zero.
With Dynamic Guidance
The following two figures show the plots of velocity error and distance between the end effector and the target during the manipulation with provided dynamic guidance. It can be seen in Figure 5 that the velocity error increases to 0.35 m/s at the beginning and then constantly reduces to and keeps at zero in 3.5 second. Figure 6 shows that the position error constantly reduces from 0.28 m to 0 in 3 seconds.
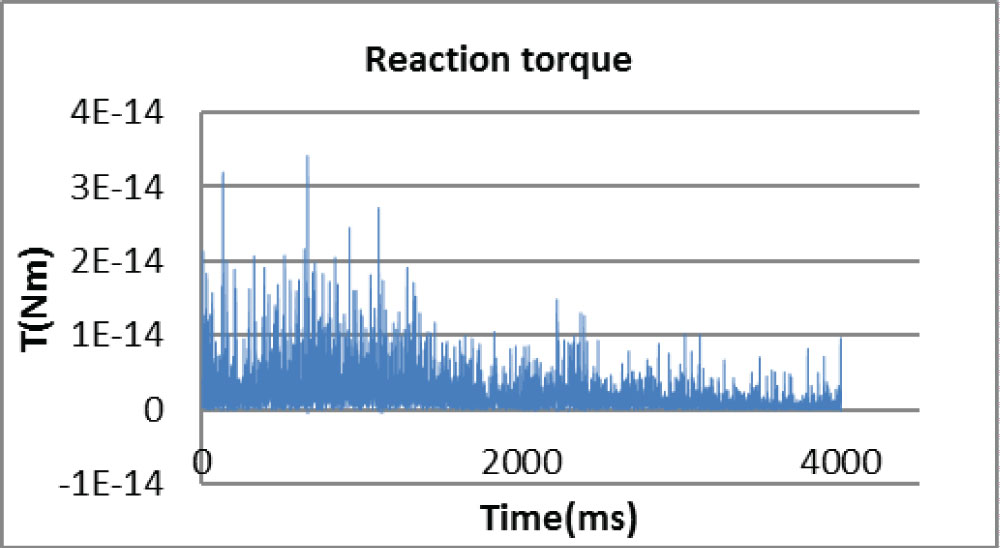
The following two figures show the reaction torque transferred to the base and the plot of the joint angles during the manipulation. Figure 7 shows that reaction torque transferred to the base is always null with some negligible numerical noise.
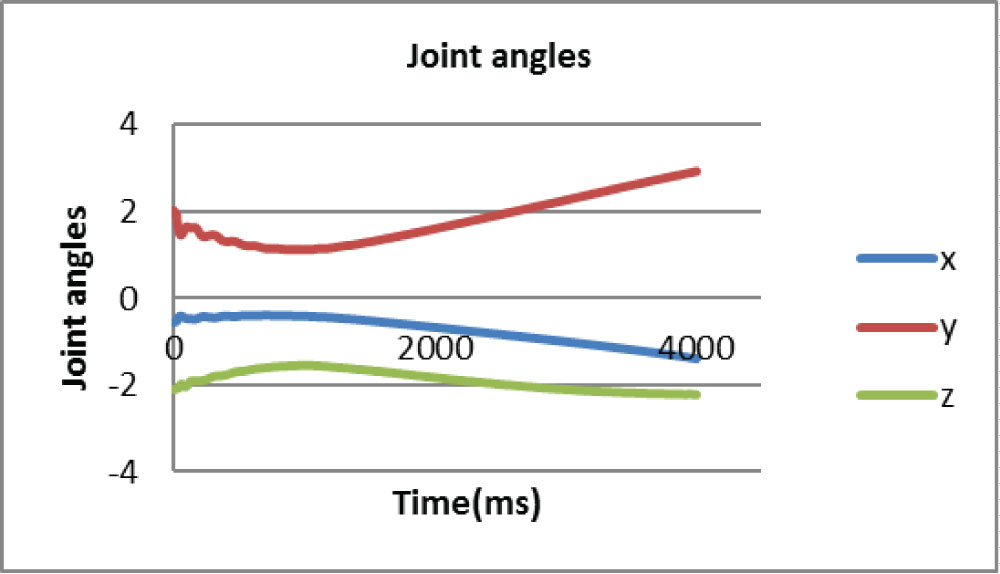
It can be seen in Figure 8 that the second joint angle has the largest rate change during the second half of the manipulation, while the changing rates of two other joint angles are relatively less.
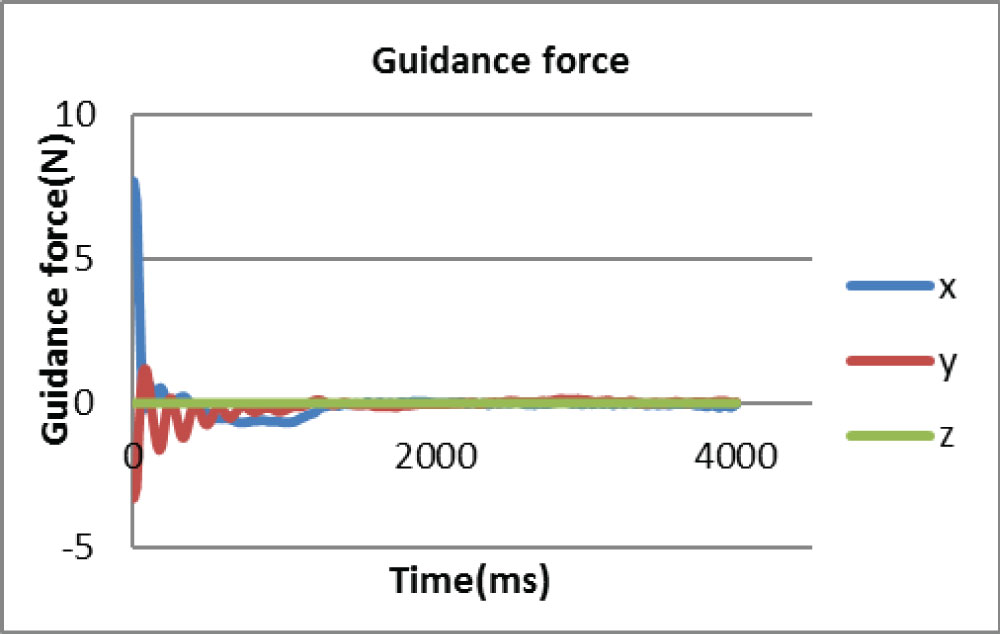
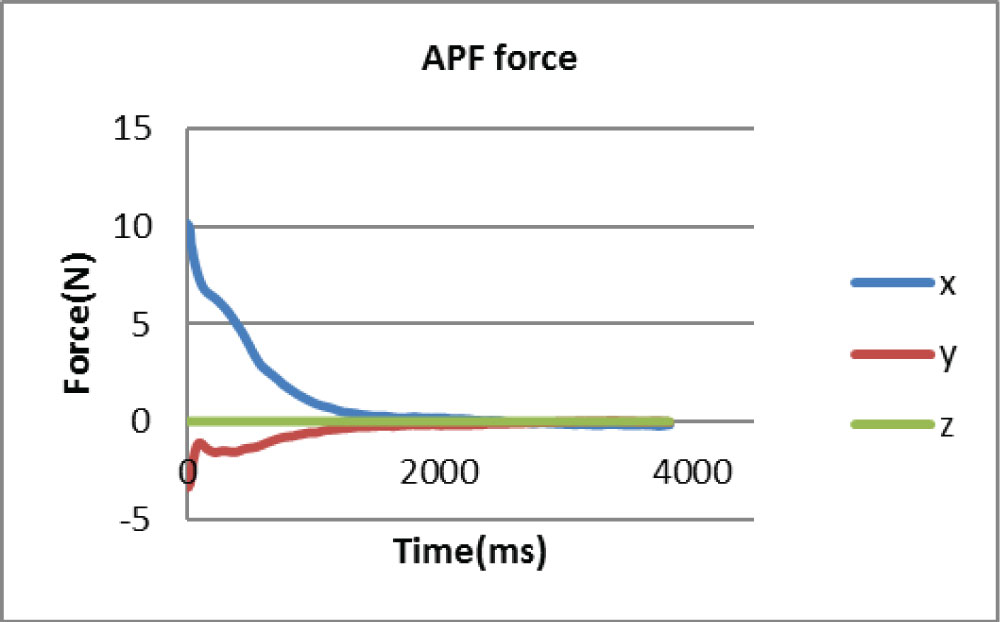
The following figure shows the plot of guidance force provided on the x axis to help a user follow the desired velocity during the operation. It can be seen in Figure 9 that the calculated guidance force on x axis starts from almost 8N, then reduces rapidly and finally stays zero after 1.5 seconds. And the calculated force on y axis starts from -3.8N and oscillates to zero in 1.5 seconds. And the plot of actuated guidance force in Figure 10 Actuated guidance force after rendering for dynamic guidance methods shows that the maximum actuated forces on x and y axis are constrained at 3N.
With Artificial Potential Field (APF) Method
To study the performance of the dynamic guidance methods, other approaches need to be compared. Therefore, a traditional guidance method using artificial potential field (AFP) is used for comparison.
Again, the participant is asked to control the manipulator to reach a target with a guidance force generated by the artificial potential field (AFP) method, which only depends on the distance to the target without considering the velocity difference. The task is still to capture the moving target at the desired velocity.
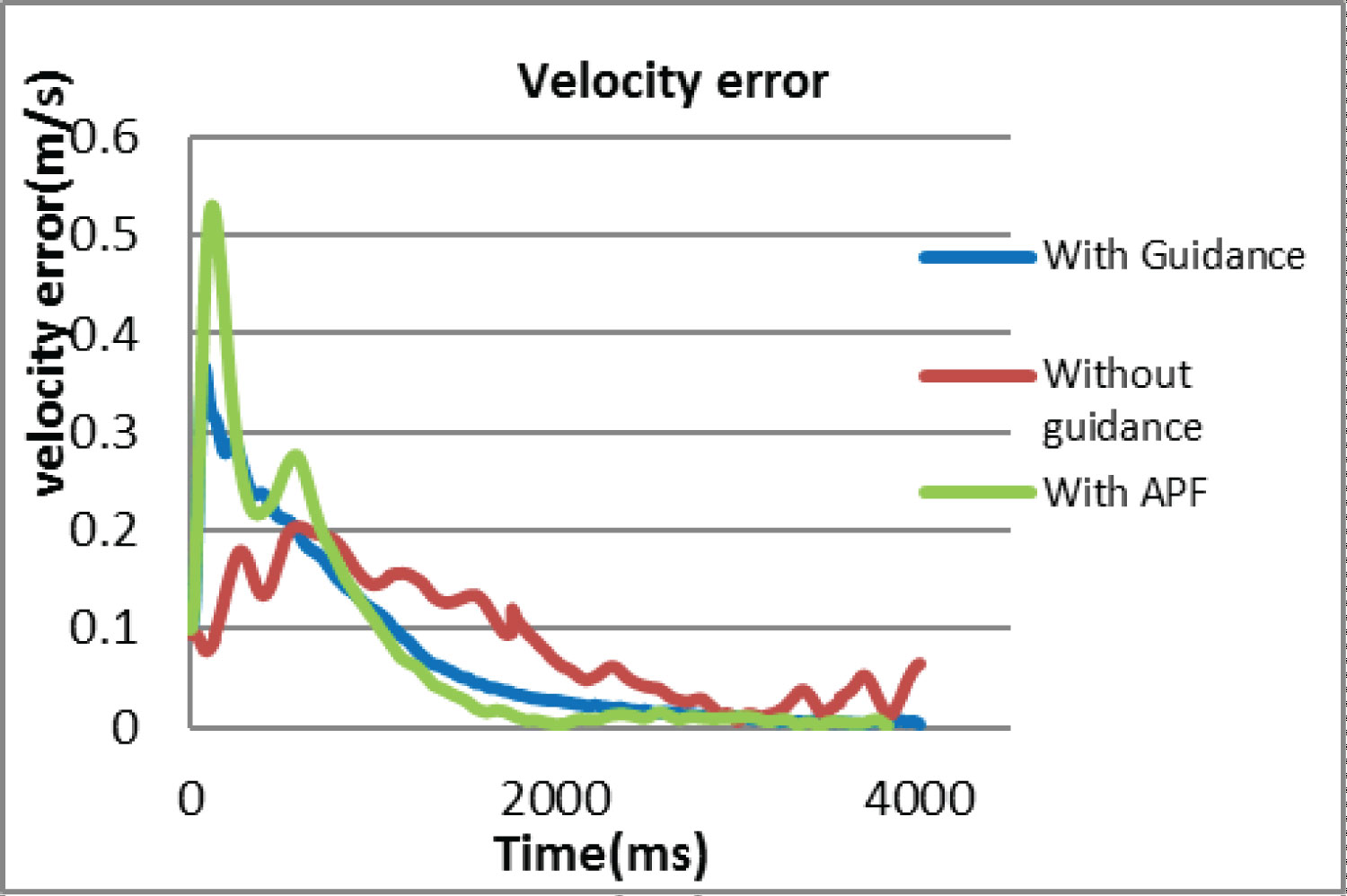
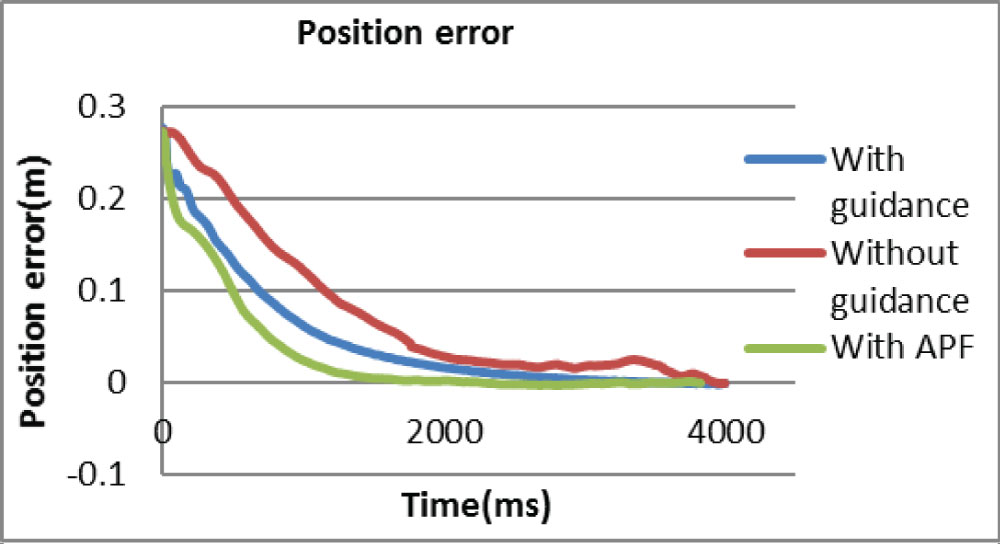
The following two figures show the comparisons of velocity errors and distances between the end effector and the target with (1) Dynamic guidance (2) No guidance (3) Artificial potential field force. In Figure 11 it can be seen that the velocity error with APF methods increase to 0.5 m/s at the beginning and then reduce to zero in 2 seconds. However it rises again and eventually comes to stay at zero after 4 seconds.
In Figure 12 it can be seen that the position error using APF methods reduces to zero constantly in 1.5 second and stays, which is faster than two other methods. In Figure 13 the travel distance of guidance and APF methods are similar, which are higher than the no guidance method until after 4 seconds they reaches the same level.
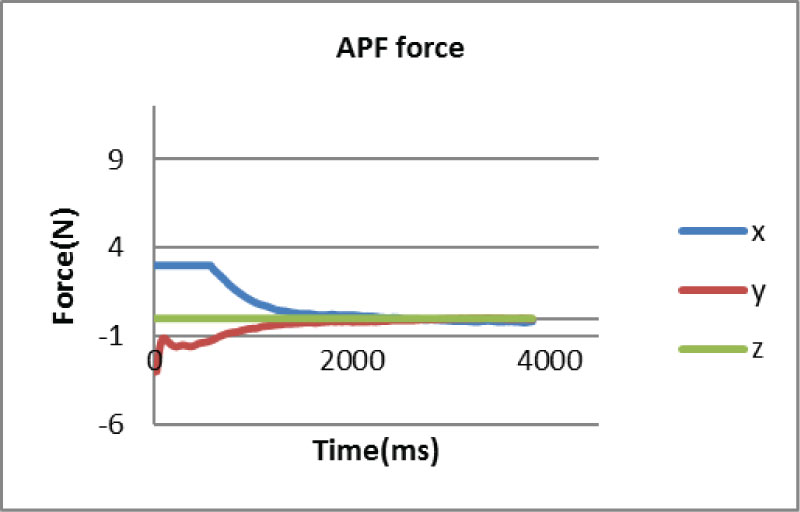
The following figures show the plot of forces provided with APF method during the capture task. In Figure 14 the calculated force on x axis starts from almost 10N, then reduces rapidly and finally stays zero after 2.5 seconds. And the calculated force on y axis starts from -3.8N and reduce to zero in 2.5 seconds. And the plot of actuated guidance force in Figure 15 shows that the maximum actuated forces on x and y axis are constrained at 3N.
Discussion of the Graphic Results
For the capturing task, in Figure 5 and Figure 6 it can be seen that the velocity error increases at the beginning, and then drops while the relative distance keeps decreasing until reaching the target. These show the combined effect of the dynamic guidance method which takes both the position error and the velocity error into account. Figure 9 shows that the guidance force on x axis is relatively large at the beginning; this is due to the large velocity and position error to the target. While the user tries to maintain control of the manipulator prevent it moving too fast, the guidance force on x axis and y axis gradually reduces with decreasing vibrations until reaching the target, which shows the effect of dynamic control of the manipulator. Moreover, Figure 7 shows that reaction torque transferred to the base is always close to null with some negligible numerical noise which meets the requirement for the space robotic manipulation.
Figure 11 and Figure 12 show the differences of performances in positions and velocities between the dynamic guidance, artificial potential field method and no guidance at all. In Figure 12 it can be seen that the potential field method reaches the target earlier than the dynamic guidance and the no guidance methods. However, Figure 11 also shows that the velocity error in potential field method isn't reaches zero at the time end effector reaching the target. It reaches zero at almost the same time as the dynamic guidance methods, while the velocity error without guidance is still unstable.
Discussion of Quantitative Results
To analyse and compare the performance of different approaches, an evaluation with quantitative result needs to be built. These quantitative results include four approaches for a space capture task: Dynamic guidance (DG), No guidance (NG), Artificial potential field (APF) and the Automatic simulation (AS). The automatic simulation takes the result of Free-shape-trajectory reactionless capture method simulated in Matlab in the last section. This is an idealised result automatically calculated by the design algorithm without any human operator's participation in the control loop, used to compare with the performance of other approaches. In each method four factors are taken into account of the analysis: (1) The time taken to reach the target (when the distance = 0), (2) The travel distance before reaching the target, (3) The MSE(mean squared error) of the relative position in 1000 ms after reaching the target, and (4) The MSE (mean squared error) of the relative velocity in 1000 ms after reaching the target. Each factor of DG, APF and no guidance methods is calculated as the mean of data collected from 3 repetitions. The results are shown in following figures.
Figure 16, Figure 17 and Figure 18 show the comparison of times, travelled distance and relative velocities at the moment of reaching the target at first time (when the distance = 0), with shown standard derivation. It can be seen that the DG method travelled the longest time and distance to reach the target, while the velocity error at the moment of reaching target (impact velocity) is lowest among three manipulation methods. The APF method reaches the target first, even faster the simulated result AS. However it has about double of the impact velocity compared to the DG, which will cause higher impact reaction. The NG method reaches the target slightly earlier than the DG, but the impact velocity is significantly higher than both the DG and APF. In addition, as can be seen from figures the NG has largest standard deviation (STDEV) which shows the instability. As a comparison the DG shows much better performance for stability with lower STDEV.
Objective Performance
Figure 19 shows the MSE (mean squared error) of the relative velocity and position in 1000 ms after reaching the target. These results are good indications of the effectiveness and stability of the performance in target capturing tasks. As shown in Figure 20 the NG method has extremely larger MSEs in both position and velocity comparing to other two methods. Therefore, to compare the results of DG and APF another graph needs to be made without NG. Figure 21 shows that the MSE of velocity in 1000 ms after capturing in DG method is significantly lower than in APF method, which indicates a better performance of stability. As for the MSE of position, APF shows a slightly better performance, however looking at the numeric level it can be concluded that both methods shows adequate performance for position following.
In summary, the developed dynamic guidance method for haptic target capturing shows adequate performance and advantages for the task. Compared to other guidance methods, the dynamic guidance shows higher effectiveness by resulting a significantly lower impact velocity at the moment of capturing and keeping a stably low MSE of velocity after the capturing. These are important factors defined by the task requirements. The efficiency of the dynamic guidance is lower than other guidance methods. It takes longer time and distance to reach target, but not significantly. Also, the impact velocity and MSE of velocity in dynamic guidance is lower than other guidance methods but still above zero. This is due to the nature of human operating comparing to automatic machine. The haptic guidance can improve stability and precision, while the manipulation is still fully controlled by the human operator.
Limitation and Future work
In this study, evaluation of the usability of the haptic guidance in space capturing tasks, a task scenario is built with an approaching target. The position and velocity of the debris target is predefined as same as in the Matlab simulation. However, the Matlab simulation is two dimensional with x and y axis. In the haptic interface and in the real working scenario, the movement of target is most likely three dimensional. Therefore in the future both the inverse kinematics solution for minimum reaction torque and haptic guidance methods need to be developed and tested in three dimensional environments. Also, validating the system with more test cases and more participants can help prove the integrity of the design and make the result more convincible. For example, the target can be set approaching from more direction at different velocities to test the usability of the proposed haptic guidance methods.
Conclusion
In this paper, a novel method for capturing a target in space using a robot with redundant degrees of freedom enabled with the assistance of haptic guidance is proposed. The proposed method is then demonstrated by means of dynamic and graphic simulations using a haptic interface to drive the robot. The developed dynamic guidance method for haptic target capturing shows adequate performance and advantages for the task. Compared to other guidance methods, the dynamic guidance shows better performance by resulting in a significantly lower impact velocity at the moment of capturing and keeping a low MSE of velocity after the capturing. The haptic guidance can improve stability and precision, while the manipulation is still fully controlled by the human operator. On the other hand this is also the most important advantage of the haptic guidance methods over automatic control, as the human operator is able to deal with emergencies and complicated situations at any time during the operation.