International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 2, Issue 1
Review Article
DOI: 10.35840/2631-5009/7507
Interstellar Travel by Hyper-Space Navigation System
Yoshinari Minami*
Figures
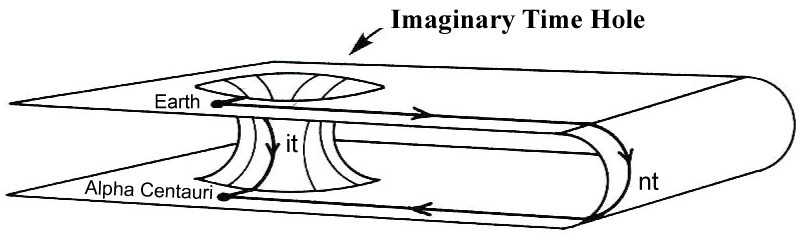
Figure 4: An Imaginary Time Hole creates....
An Imaginary Time Hole creates a shortcut from Earth to Alpha Centauri.
References
- Y Minami (1993) Hyper-Space Navigation Hypothesis for Interstellar Exploration. 44th Congress of the International Astronautical Federation (IAF), Australia.
- Minami Y (2003) Travelling to the Stars: Possibilities Given by a Spacetime Featuring Imaginary Time. JBIS 56: 205-211.
- Minami Y (2005) A Perspective of Practical Interstellar Exploration: Using Field Propulsion and Hyper-Space Navigation Theory. In: Mohamed S El-Genk, Space Technology and Applications International Forum. AIP Conference Proceedings, Melville, New York, 746: 1419-1429.
- Minami Y (2014) A Journey to the Stars: By Means of Space Drive Propulsion and Time-Hole Navigation. LAMBERT Academic Publishing.
- Minami Y (2014) Interstellar travel through the Imaginary Time Hole. Journal of Space Exploration 3: 206-212.
- Minami Y (2015) Space propulsion physics toward galaxy exploration. J Aeronaut Aerospace Eng 4: 2.
- Forward RL (1989) Space Warps : A Review of One Form of Propulsionless Transport. JBIS 42: 533-542.
- Froning Jr, H.D (1983) Requirements for Rapid Transport to the Further Stars. JBIS 36: 227-230.
- Froning Jr, H.D (2016) The Halcyon Years of Air and Space Flight: And the Continuing Quest. LAMBERT Academic Publishing.
- Hawking S (1988) A Brief History of Times. Bantam Publishing Company, New York.
- Hawking S (1993) Hawking on the Big Bang and Black Holes. World Scientific 8.
- Williams C, Cardoso JG, Whitney CK, Minami Y, Mabkhout SA, et al. (2015) Advances in general relativity research. Nova Science Publishers.
Author Details
Yoshinari Minami*
Advanced Science Technology Research Organization, Formerly NEC Space Development Division, Japan
Corresponding author
Yoshinari Minami, Advanced Science-Technology Research Organization, Formerly NEC Space Development Division, 35-13, Higashikubo-Cho, Nishi-Ku, Yokohama, 220-0062, Japan, E-mail: [email protected]
Accepted: May 27, 2017 | Published Online: May 29, 2017
Citation: Minami Y (2017) Interstellar Travel by Hyper-Space Navigation System. Int J Astronaut Aeronautical Eng 2:007.
Copyright: © 2017 Minami Y. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
An interstellar travel within a human lifetime is considered as utterly impossible. The interstellar travel used Special Relativity is well known. However, there exists the problem of the twin or time paradox. In addition, although space warp using wormhole is also well known, the size of the wormhole is smaller than the atom, and moreover, the wormhole is predicted to fluctuate theoretically due to instabilities. Assuming Hyper-Space as being characterized by imaginary time, it is shown that the limitations due to the extremely long time required for interstellar travel are removed. The Hyper-Space navigation theory discussed here would allow a starship to start at any time and from any place for an interstellar travel to the farthest star systems, the whole mission time being within human lifetime.
This newly added paper introduces a realistic method of the interstellar travel (i.e., Hyper-Space navigation) based on the concept published so far by author [1-6].
Keywords
Interstellar travel, Space-time, Imaginary time, Hyper-Space, Wormhole, Special Relativity, Time-hole
Introduction
As is well known in astronomy, sixty-three stellar systems and other eight hundred fourteen stellar systems exist respectively within the range of 18 and 50 light years from our Solar System. For instance, Alpha Centauri is the nearest star from Earth, and the star Sirius, which is the seventh nearest star, is 8.7 light years from Earth, while the Pleiades star cluster is 410 light years from us. According to Einstein's Special Relativity, sending a starship to a stellar system at a distance longer than several hundred light years would ask for an extremely long time even if the starship would travel at the speed of light. For instance, assuming that the starship is traveling to the Pleiades star cluster at a speed of 0.99999c, it will arrive at the Pleiades 1.8 years later and, in the case of immediately starting of the return travel, it would be back to Earth 3.6 years after leaving for the Pleiades. But this would be just for the clocks of the astronauts onboard the starship for that mission. For people on Earth, the whole time period would be 820 years, with paradoxical consequences as to the feasibility of a mission such as this. The first solution of the above-stated problem is to obtain a breakthrough in propulsion science. However, from the standpoint of propulsion theory using not only momentum thrust but also pressure thrust, there is no propulsion theory which exceeds the speed of light, even if we use the field propulsion theory. Accordingly, the propulsion theory alone is not enough to establish the reality of interstellar travel, thereby requiring a navigation theory as a secondary solution.
Concerning interstellar travel, the method using a wormhole is well known; relying on space warps, such as for instance Wheeler-Planck Wormholes, Kerr metric, Schwartzschild metric, Morris-Thorne Field-Supported Wormhole based on the solutions of equations of General Relativity [7]. However, since the size of wormhole is smaller than the atom , i.e., ~ m and moreover the size is predicted to fluctuate theoretically due to instabilities, space flight through the wormhole is difficult technically and it is unknown where to go and how to return. Additionally, since the solution of wormhole includes a singularity, this navigation method theoretically includes fundamental problems. The search for a consistent quantum theory of gravity and the quest for a unification of gravity with other forces (strong, weak, and electromagnetic interactions) have both led to a renewed interest in theories with extra spatial dimensions. Theories that have been formulated with extra dimensions include Kaluza-Klein theory, supergravity theory, superstring theory, and M theory, D-brane theory related superstring. For instance, superstring theory is formulated in 10 or 26 dimensions (6 or 22 extra spatial dimensions). These extra spatial dimensions must be hidden, and are assumed to be unseen because they are compact and small, presumably with typical dimensions of the order of the Planck length (~10-35 m). The navigation method of utilizing extra dimensions (even if they are compactified) has also a theoretical problem as well as using a wormhole.
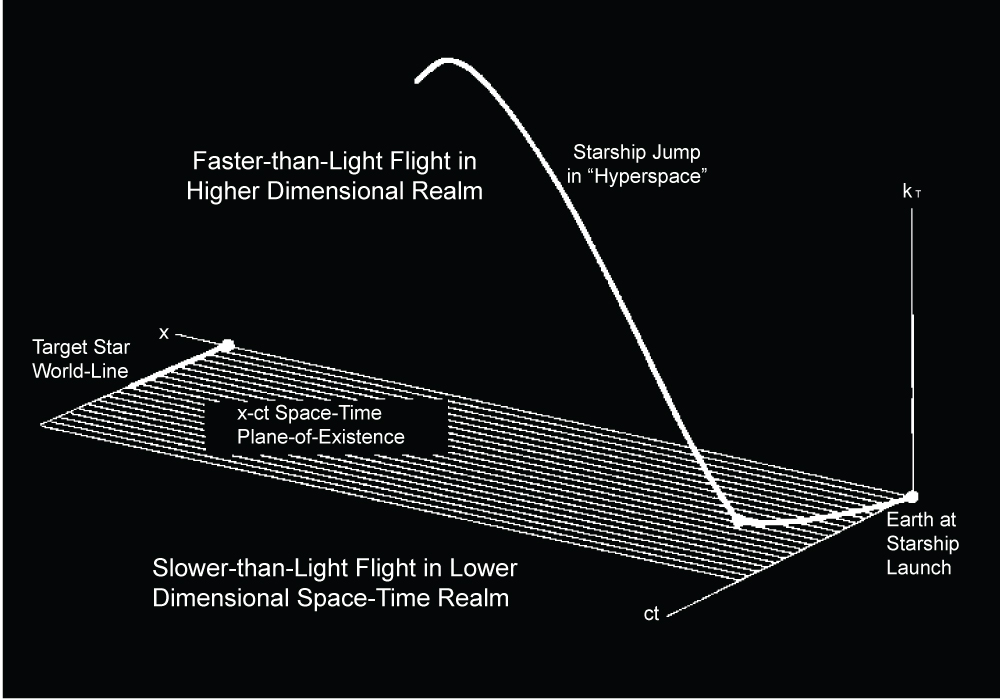
On the one hand, there exists another interstellar navigation theory. Froning showed the rapid starship transit to a distant star (i.e. Instantaneous Travel) using the method of "jumping" over so-called time and space [8,9] (Figure 1).
This idea is based on "tachyons" which could go Faster Than Light (FTL). And some viewed tachyons as faster-than-light solutions of Einstein's Special Relativity (SR). For, SR's Lorentz contraction factor [(1-(V/c)2]1/2 has real values only for speed V Slower Than Light (STL). But, if multiplied by i = [-1]1/2 (imaginary unit), this factor becomes [(V/c)2-1]1/2 which has real values only for FTL speed. Figure 1 shows the plane of existence of ordinary x-ct space-time. This was with a vertical coordinate ikτ, which is orthogonal to those which describe space travel (x) and time travel (ct) of slower-than-light tachyons on an x-ct space-time plane of existence. And this x-ct plane is seen to be embedded in the volume of the higher-dimensional x-ct-ikτ realm rising above it.
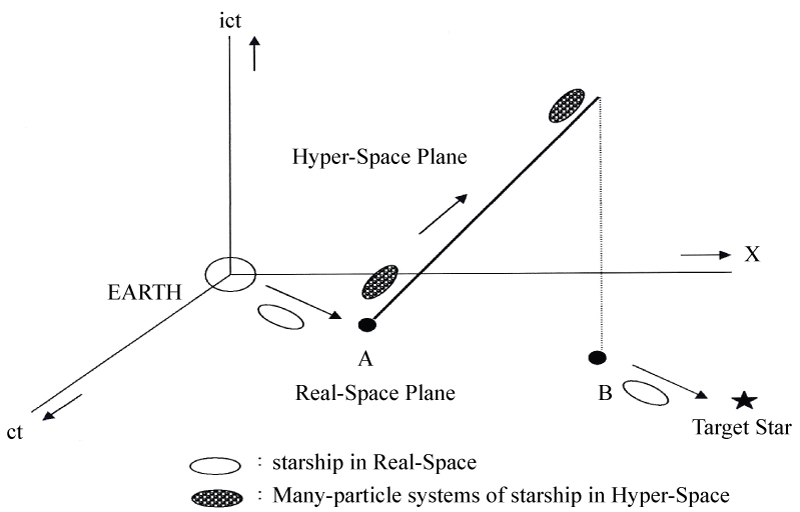
In addition to this invaluable concept, Minami studied its own navigation theory independently and proposed the Hyper-Space navigation theory using a space-time featuring an imaginary time [1-6] (Figure 2). Hyper-Space navigation theory using a space-time featuring an imaginary time offers a great promise to develop practical interstellar exploration. Although it seems to be similar in using imaginary time, it is based on a totally different theory from Tachyon. This proposed navigation theory is based on Special Relativity (not on General Relativity), that allows interstellar travel to the farthest star systems to be realized; and removes the present theoretical limitations to interstellar travel that arises from the extremely long time needed (the time paradox) according to Special Relativity.
By the way, imaginary time is a difficult concept to grasp, and it is probably much difficulty that has caused most problems. How can imaginary time have anything to do with the real universe? Stephen Hawking has been working at developing equations that would tell us just what did happen when time began. The concept of imaginary time is related to the origin and fate of the universe. His theories use such concepts as imaginary time and singularities to unite relativity and quantum physics [10,11].
As to Feynman's sum over histories, to avoid some technical difficulties, one must use imaginary time. In real time, the universe has a beginning and an end at singularities that form a boundary to space-time at which the laws of science break down. But in imaginary time, there are no singularities and boundaries. This might suggest that the so-called imaginary time is really more basic.
The practical interstellar travel combines propulsion theory with navigation theory. In the following chapters, Hyper-Space navigation theory is described in detail.
Three ways to the interstellar travel
Three methods are considered to reach the star rapidly. The basic principle is the following equation which is known to every one:
Where, Lstar is the distance to star, Vstarship is the speed of starship, t is the time.
The distance to a stellar system "Lstar" is enormous. An extremely long time is required, even if the starship would travel at the speed of light "c". To reach the star rapidly, three parameters, such as "speed", "distance" and "time", shall be controlled.
Change speed
Where, "nc" is n-fold increase in speed of light "c". Here, n is real number greater than 1.
There is no propulsion theory exceeds the speed of light, moreover, Special Relativity restricts the maximum speed to the speed of light; therefore this method is impossible.
Change distance
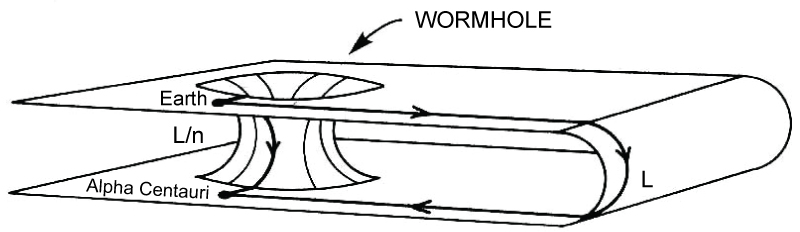
The so-called "wormhole" is utilized. By using wormhole, shorten the distance as a few meters, as shown in Figure 3. For example, one meter in a wormhole corresponds to a few light years in actual space.
Change time
The time "t" in an imaginary time hole is equivalent time of n-fold time in actual space, as shown in Figure 4. For example, one second in an imaginary time hole corresponds to one million seconds in actual space. Subsequently, interstellar travel through the imaginary time hole is described as the following.
Properties of flat space
In general, the property of space is characterized by a metric tensor that defines the distance between two points. Here space is divided into two types. Actual physical space that we live in is a Minkowski space, and the world is limited by Special Relativity. It is defined as "Real-Space". Here as a hypothesis, an invariant distance for the time component of Minkowski metric reversal is demanded. This is not a mere time reversal. It is defined as "Hyper-Space". The invariance is identical with the symmetries. Symmetries in nature play many important roles in physics. From this hypothesis, the following arises: the properties of the imaginary time (x0 = ict; i2 = -1) are required as a necessary result in Hyper-Space. Here, "i" denotes the imaginary unit and "c" denotes the speed of light. The time "t" in Real-Space is changed to imaginary time "it" in Hyper-Space. However, the components of space coordinates (x, y, z) are the same real numbers as the Real-Space. From the above, it is seen that the real time (x0 = ct) in Real-Space corresponds to the imaginary time (x0 = ict) in Hyper-Space. That is, the following is obtained:
Real-Space: t (real number), x, y, z (real number); Hyper-Space: it (imaginary number; i2 = -1), x, y, z (real number).
The imaginary time direction is at right angles to real time. This arises from the symmetry principle on the time component of Minkowski metric reversal (Appendix).
Lorentz transformation of Hyper-Space
Next, the Lorentz transformation of Hyper-Space corresponding to that of Real-Space is found.
Since the components of space coordinates (x, y, z) do not change between Real-Space and Hyper-Space, the velocity in Hyper-Space can be obtained by changing t → it:
The velocity becomes the imaginary velocity in Hyper-Space. Substituting "t → it, V → -iV" into the Lorentz transformation equations of Minkowski space formally gives:
Hyper-Space lorentz transformation
This result agrees with the results of detailed calculation. As a reference, the Lorentz transformation equations of Minkowski space, i.e. of Special Relativity, are shown below:
Real-Space lorentz transformation
Special Relativity
The main difference is that the Lorentz-Fitz Gerald contraction factor is changed to .
Now, consider navigation with the help of both Lorentz transformations, especially the Lorentz contraction of time.
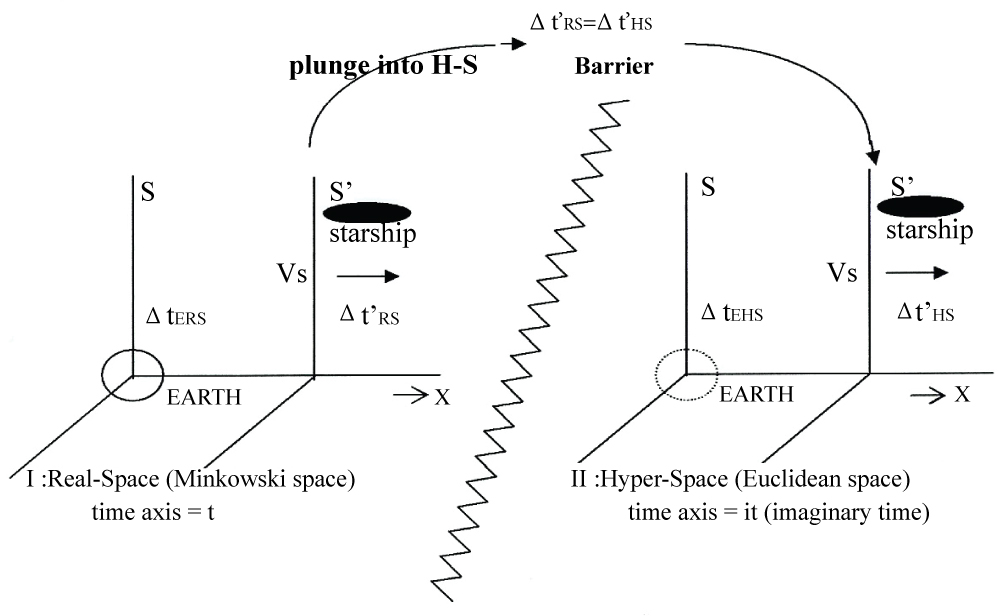
Figure 5 shows a transition of starship from Real-Space to Hyper-Space. In Figure 5, region I stands for Real-Space (Minkowski space). Consider two inertial coordinate systems, S and S'. S' moves relatively to S at the constant velocity of starship (VS) along the x-axis. S' stands for the coordinate system of the starship and S stands for the rest coordinate system (VS = 0) on the earth. ΔtERS is the time of an observer on the earth, i.e. earth time, and Δt'RS is the time shown by a clock in the starship, i.e. starship time. Region II stands for Hyper-Space (Euclidean space). S' moves relatively to S at the constant velocity of starship (VS) along the x-axis. S' stands for the coordinate system of the starship in Hyper-Space and S stands for the rest coordinate system (VS = 0) in Hyper-Space. ΔtEHS is the time of an observer on the earth in Hyper-Space, i.e. the equivalent earth time, and Δt'HS is the time shown by a clock in the starship in Hyper-Space, i.e. the starship time. Now, the suffix."HS" denotes Hyper-Space and the suffix."RS" denotes Real-Space. Figure 5 also shows a linear mapping f:RS (Real-Space)→HS (Hyper-Space), that is, from a flat Minkowski space-time manifold to a flat imaginary space-time manifold. It is assumed that space is an infinite continuum [12]. There exists a 1-1 map f:RS→HS, xi|→f(xi) and a 1-1 inverse map f-1:HS→RS, f(xi)|→xi. The mapping is a bijection. These transformations will be local and smooth.
Now suppose that a starship accelerates in Real-Space and achieves a quasi-light velocity (VS ~ c) and plunges into Hyper-Space by some new technical methods. Here, "plunges into Hyper-Space" means "transition from Real-Space to Hyper-Space", or is often said to be "Jump" or "pass through the barrier separating Real-Space from Hyper-Space". In Real-Space, from Eq.(3),
Eq.(4) is the so-called Lorentz contraction of time derived from Special Relativity. In Hyper-Space, the starship keeps the same velocity as the quasi-light velocity (VS ~ c) just before plunging into Hyper-Space, i.e. VS(HS) = VS(RS). Therefore, from Eq.(2),
From Figure 5, after plunging into Hyper-Space, the starship keeps the quasi-light velocity and takes the S' coordinates. The elapsed time in the starship will be continuous. Considering the continuity of starship time between Real-Space and Hyper-Space, we get
Now Eq.(6) gives, from Eqs.(4) and (5),
Eq.(7) is the time transformation equation of earth time between Real-Space and Hyper-Space. From Eq.(7), when VS = 0, we get
Namely, in the reference frame at rest, the elapsed time on the earth coincides with both Real-Space and Hyper-Space. However, as the velocity of starship approaches the velocity of light, the earth time between Real-Space and Hyper-Space becomes dissociated on a large scale.
Since an observer on the earth looks at the starship going at VS ~ c and loses sight of it as it plunges into Hyper-Space, it is observed that the starship keeps the same velocity and moves during the elapsed time ΔtERS (at VS ~ c) observed from the earth. Therefore, the range of starship of an observer on the earth is given by
From Figure 5, after plunging into Hyper-Space, the starship keeps the quasi-light velocity and takes the S' coordinates. The elapsed time in the starship will be continuous. Considering the continuity of starship time between Real-Space and Hyper-Space, we get
For instance, in the case of VS = 0.999999999c, from Eqs. (7) and (5), we get
One second in Hyper-Space corresponds to 31,622 seconds in Real-Space. Similarly, one hour in Hyper-Space corresponds to 31,622 hours (3.6 years) in Real-Space.
While the starship takes a flight for 100 hours (Δt'HS = 100 hr; VS = 0.999999999c) shown by a clock in the starship in Hyper-Space, 70 hours (ΔtEHS = 70 hr; VS = 0) have elapsed on the earth in Hyper-Space. Since this elapsed time on the earth in Hyper-Space is in the reference frame at rest, the time elapsed in it is the same as the time elapsed on the earth in Real-Space ( [ΔtEHS; VS = 0] = [ΔtERS;VS = 0] = 70 hr). Therefore, there is not much difference between the elapsed time (70 hours) of an observer on the earth in Real-Space and the elapsed time (100 hours) of starship during Hyper-Space navigation. However, this elapsed time of 70 hours (ΔtEHS = 70 hr; VS = 0) on the earth in Hyper-Space becomes the elapsed time of 253 years (ΔtERS = 70 × 31,622 = 2,213,540 hr; VS = 0.999999999c) on the earth in Real-Space, because the starship flies at the velocity of 0.999999999c. These 253 years represents the flight time of starship observed from the earth in Real-Space. Therefore, by plunging into Hyper-Space having the properties of imaginary time, from Eq.(9), the starship at a quasi-light velocity can substantially move a distance of approximately 253 light years. In this way, the starship at a quasi-light velocity can travel to the stars 253 light years away from us in just 100 hours.
The above numerical estimation depends on the velocity of starship. For instance, in the case of VS = 0.99999c, we get
On the contrary, in the case of VS = 0.999……999c, a gap between ΔtERS and ΔtEHS rapidly increases. That depends on how the starship can be accelerated to nearly the velocity of light.
Star flight for stellar system
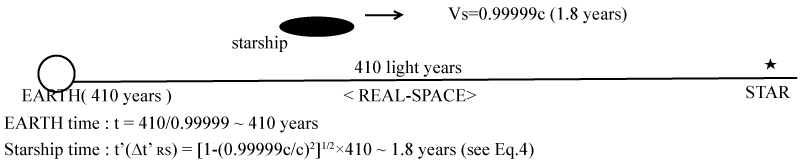
Next, a comparison is made between interstellar travel by Special Relativity and Hyper-Space Navigation. The condition is the same for both cases of navigation, that is, the distance between the earth and the star is 410 light years (i.e. Pleiades star cluster) and the velocity of starship is 0.99999c.
Special relativity allows the following (Figure 6)
A starship can travel to stars 410 light years distant from us in 1.8 years. However, there exists a large problem as is well known, i.e., the twin, or time, paradox. If the starship travels at a velocity of 0.99999c, it will arrive at the Pleiades star cluster 1.8 years later. It will seem to the crews in the starship that only 1.8 years have elapsed. But to the people on earth it will have been 410 years. Namely, since the time gap between starship time and earth time is so large, the crew coming back to the earth will find the earth in a different period. This phenomenon is true in our Real-Space. Interstellar travel by this method is non-realistic, i.e., it would just be a one-way trip to the stars.
Hyper-Space navigation allows the following (Figure 7)
A starship can travel to the stars 410 light years distant in 1.8 years. During Hyper-Space navigation of 1.8 years, just 1.3 years have passed on the earth. Therefore, the time gap between starship time and earth time is suppressed. After all, the range and travel time of starship is the same for both kinds of navigation, and travel to the stars 410 light years away can occur in just 1.8 years in both cases. However, by plunging into Hyper-Space featuring an imaginary time, i.e. a Euclidean space property, just 1.3 years, not 410 years, have passed on the earth. There is no time gap and no twin or time paradox such as in Special Relativity. Additionally, a starship can travel to the star Sirius 8.7 light years distant us in 0.039 years (14 days). During Hyper-Space navigation of 14 days, just 0.028 years (9 days) have passed on the earth.
Figure 8 shows such a realistic method for the interstellar travel using Hyper-Space navigation system (i.e., Time Hole; Figure 4). In order to reach the target star, the starship which left the earth at a velocity of approximately 0.1c to 0.2c moves and escapes completely from the Solar System (with Figure 8). After that, the starship is accelerated to nearly the speed of light in Real-Space and plunges into Hyper-Space at point A. In Hyper-Space, the time direction is changed to the imaginary time direction and the imaginary time direction is at right angles to real time. The course of starship is in the same direction, i.e. x-axis. With the help of Eqs. (5), (7) and (9), the crew can calculate the range by the measurement of starship time. After the calculated time has just elapsed, the starship returns back to Real-Space from Hyper-Space at a point B nearby the stars. Afterward, the starship is decelerated in Real-Space and reaches the target stars. It is immediately seen that the causality principle holds. Indeed, the starship arrives at the destination ahead of ordinary navigation by passing through the tunnel of Hyper-Space (Time Hole). The ratio of tunnel passing time to earth time is 1.4:1 and both times elapse. Hyper-Space navigation method can be used at all times and everywhere in Real-Space without any restrictions to the navigation course.
This implies that Real-Space always coexists with Hyper-Space as a parallel space. The factor that isolates Real-Space from Hyper-Space consists in the usual-experience "real time" of the former as opposed to the "imaginary time" characterizing the latter. And each space is isolated by the potential barrier (Figure 5).
In general, in case that a diverse two kinds of phase space coexist or adjoin, a potential barrier shall exist to isolate these two kinds of phase space. Starship shall overcome the potential barrier by some methods. One and only difference is either real time or imaginary time. The Real-Space (3 space axes and 1 time axis) and Hyper-Space (3 space axes and 1 imaginary time axis) coexist; the parallel space-time exists as a five dimensional space-time (3 space axes and 2 time axes). Concerning a concept on technical method of plunging into Hyper-Space and returning back to Real-Space, the following study is necessary: 1) Many-Particle Systems for Starship, 2) Wave function of Starship by Path Integrals, 3) Quantum Tunneling Effect, 4) Reduction of Wave function, 5) Starship Information Content Restoring.
While the conceptual framework discussed above is highly speculative, it is in the wake of most of the current international trends on the subject of "Interstellar Travel". Indeed, the problem of interstellar travel consists much more in a navigation theory than in propulsion, as there is no propulsion theory, capable of causing a starship to travel at a velocity faster than the speed of light.
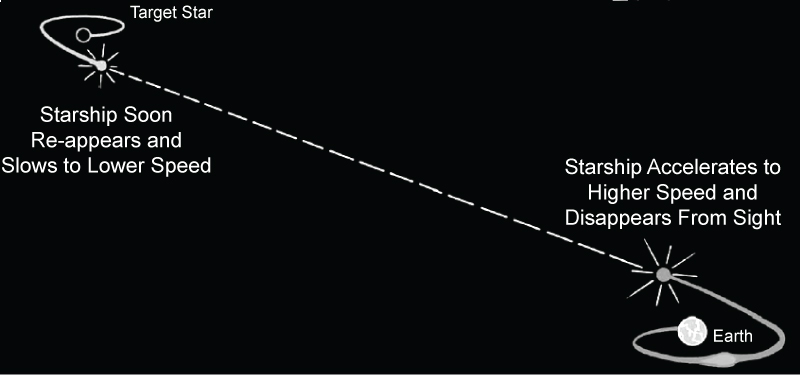
Also, Figure 9 schematically shows the navigation of Figure 8.
Starship accelerates away from Earth, disappears and re-appears after Hyper-Space navigation. But during these Hyper-Space navigation of disappearance, the starship, in effect, leaps high above space-time and over stupendous distances to reach speeds that are substantively billions of times light-speed.
Starship flight can also be viewed from the perspective of an Earth observer who is watching a starship fly away - accelerating in the direction of its target (a planet in another solar system) and then vanishing from sight as its initial acceleration ends. The starship then re-appears after Hyper-Space navigation - at the speed it disappeared at. But the starship is now suddenly 400 light-years away - very near to its destination. By plunging into Hyper-Space featuring an imaginary time (i.e., Imaginary Time Hole), the starship detours the imaginary time tunnel (Figure 4), apparently exceeds the speed of light.
Comparison of Wormhole and Time-Hole
Finally we compare the navigation features of the wormhole and the time-hole as shown in Table 1.
Both navigation methods allow interstellar travel in a short period of time, but the features of the navigation, theoretical and technical issues are different.
Conclusions
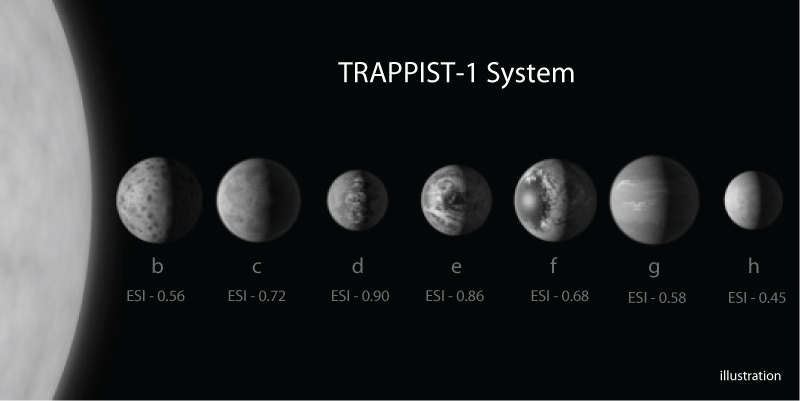
Just recently (Feb. 23, 2017), NASA announced that seven planets resembling the Earth were discovered at 40 light years distant from us. Three of these planets are firmly located in the habitable zone, the area around the parent star where a rocky planet is most likely to have liquid water.
Seven Earth-sized planets have been observed by NASA's Spitzer Space Telescope around a tiny, nearby, ultra-cool dwarf star called TRAPPIST-1 (Figure 10).
The depth of the transits provides a measurement of the radius of the planets, which are similar to Earth (b, c, e, f, g) or Mars (d, h) so they range from 75% to 110% the size of Earth.
This exoplanet system at 40 light-years from Earth seems to be relatively close to us, but we cannot go to there due to lack of advanced propulsion system and navigation system. We need the practical space travel means which combines both space propulsion theory with space navigation theory.
As described above, a plunging into Hyper-Space characterized by imaginary time would make the interstellar travel possible in a short time. We may say that the present theoretical limitation of interstellar travel by Special Relativity is removed. The Hyper-Space navigation theory discussed above would allow a starship to start at any time and from any place for an interstellar travel to the farthest star systems, the whole mission time being within human lifetime (Figure 11).