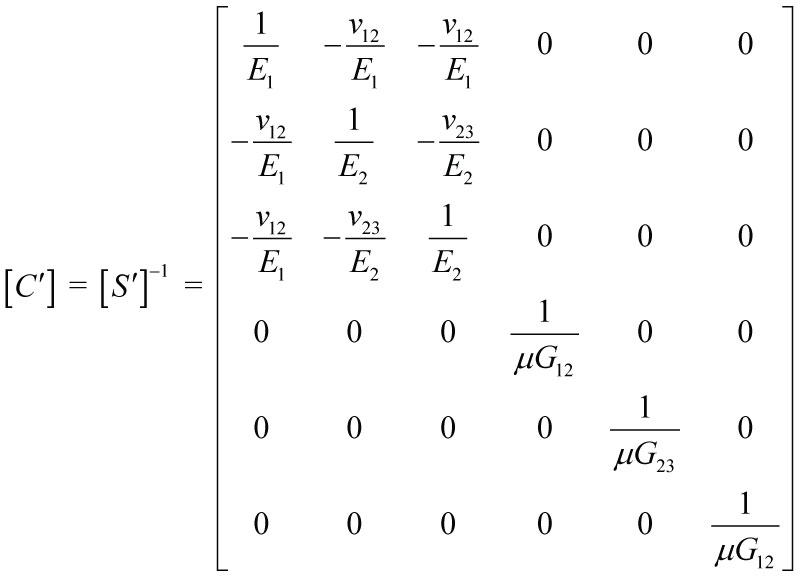International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 2, Issue 1
Review Article
DOI: 10.35840/2631-5009/7506
Blast Reinforcing of Unit Load Device Using High Modulus Polypropylene Plain Weave Fabrics
S Kilimtzidis, A Kotzakolios and V Kostopoulos*
Table of Content
Figures

Figure 8: Numerical model of the tested...
Numerical model of the tested fabric and the experimental device.

Figure 16: Von mises stresses (Pa)...
Von mises stresses (Pa) at the ULD after 1 ms of m0blast loading.
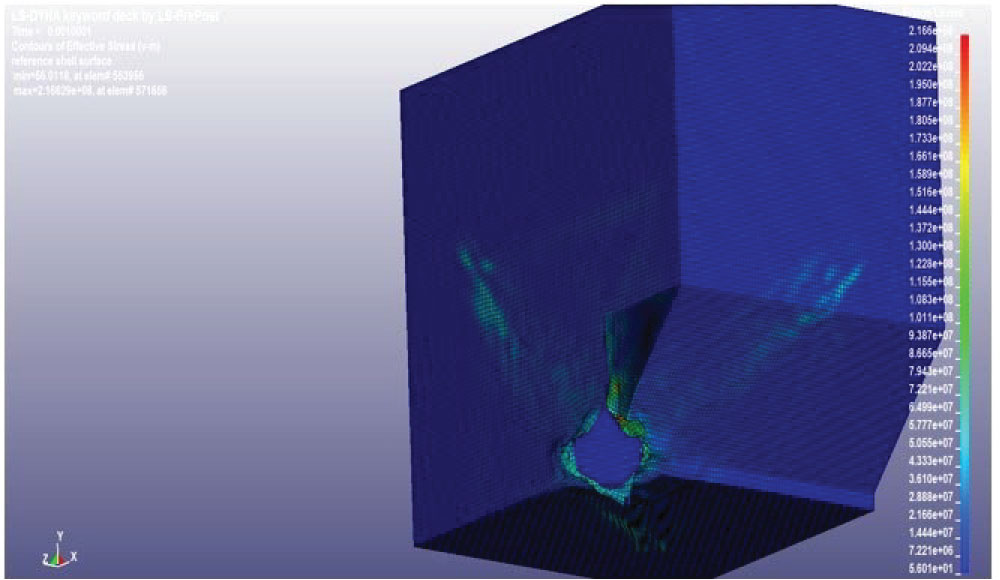
Figure 17: Von mises stresses...
Von mises stresses (Pa) at the Innegra layer after 1 ms of blast loading, one fabric layer modeled.

Figure 18: Von Mises stresses (Pa)...
Von Mises stresses (Pa) at the Innegra layers after 1 ms, two fabric layers modeled.
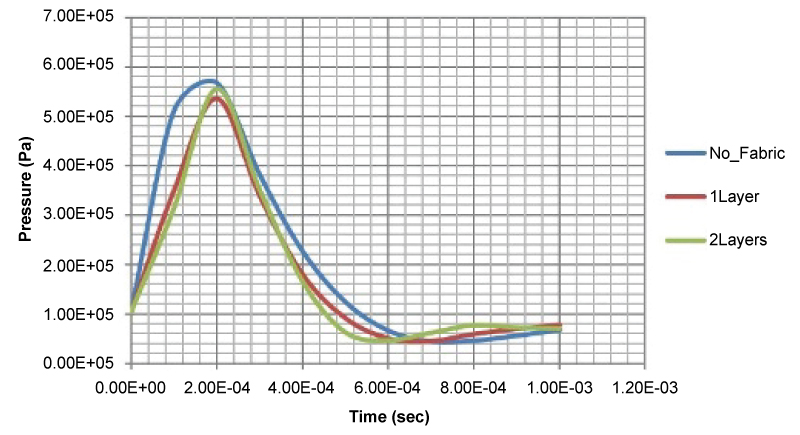
Figure 19: Pressure (Pa) versus time...
Pressure (Pa) versus time (s) diagrams in the case of explosive mass of m0.
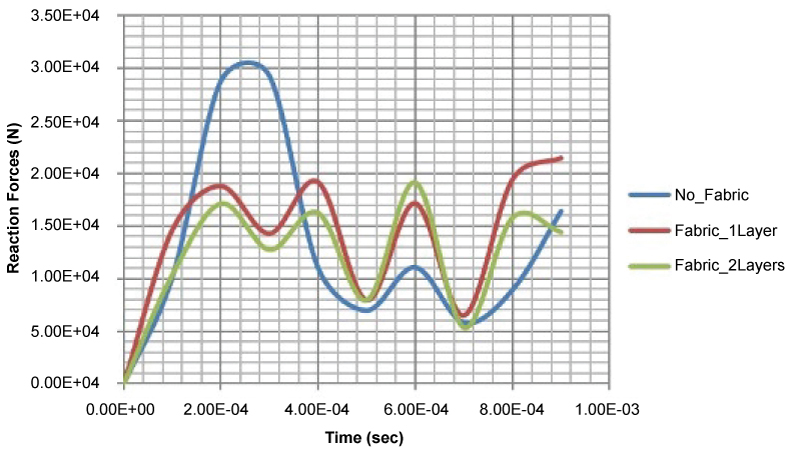
Figure 20: Reaction forces (N) versus...
Reaction forces (N) versus time (s) diagrams for the m0 blast loading.
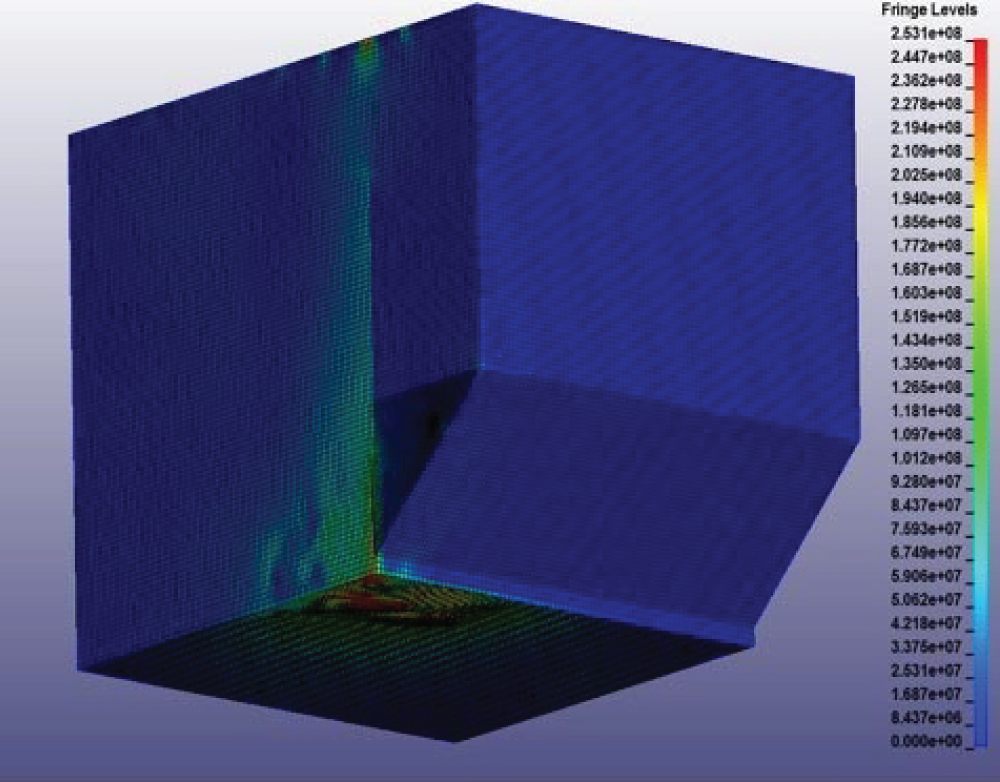
Figure 21: Von mises stresses (Pa)...
Von mises stresses (Pa) at the ULD after 1 ms of 2m0 blast loading.

Figure 22: Von mises stresses...
Von mises stresses (Pa) at the innegra layer after 1 ms of 2m0 blast loading.

Figure 23: Von mises stresses (Pa)...
Von mises stresses (Pa) at the innegra layers after 1 ms of 2m0 blast loading.
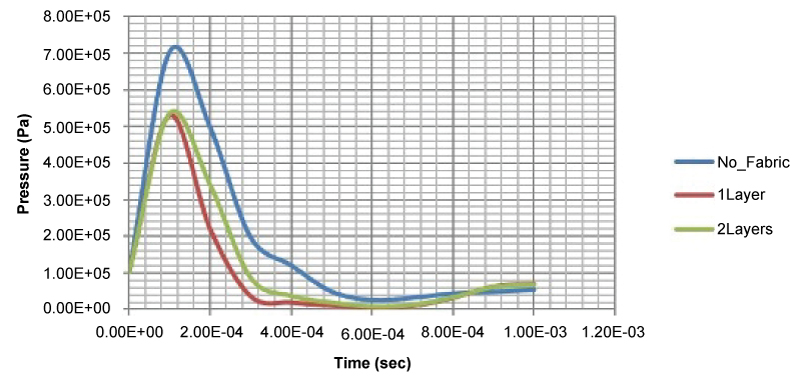
Figure 24: Pressure (Pa) versus...
Pressure (Pa) versus time (s) diagrams for the 2m0 blast loading.
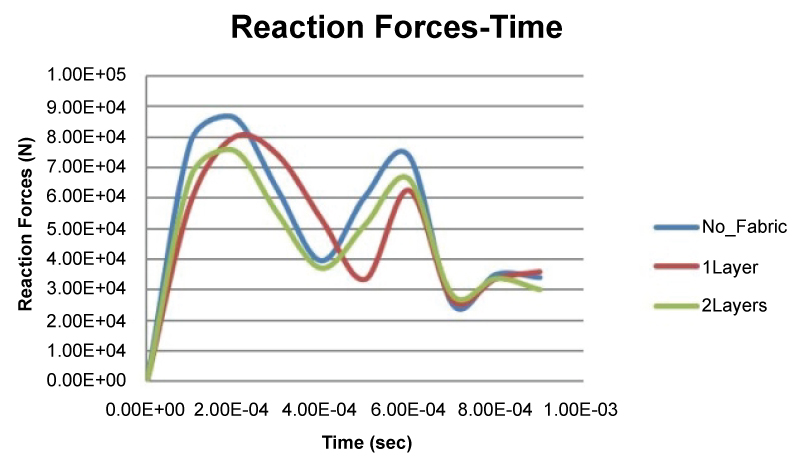
Figure 25: Reaction forces (N)...
Reaction forces (N) versus time (s) diagrams in the case of explosive mass of 2m0.

Figure 26: Von mises stresses (Pa) at...
Von mises stresses (Pa) at the ULD after 1 ms of 3m0 blast loading.
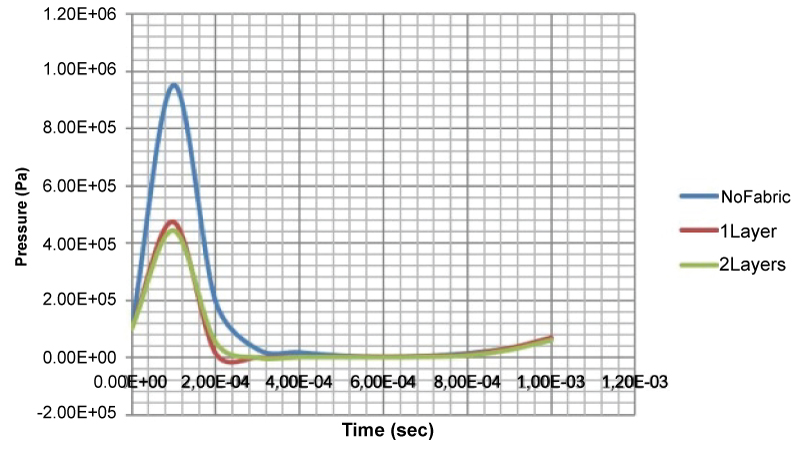
Figure 27: Pressure versus time diagrams...
Pressure versus time diagrams in the case of explosive mass of 3m0.
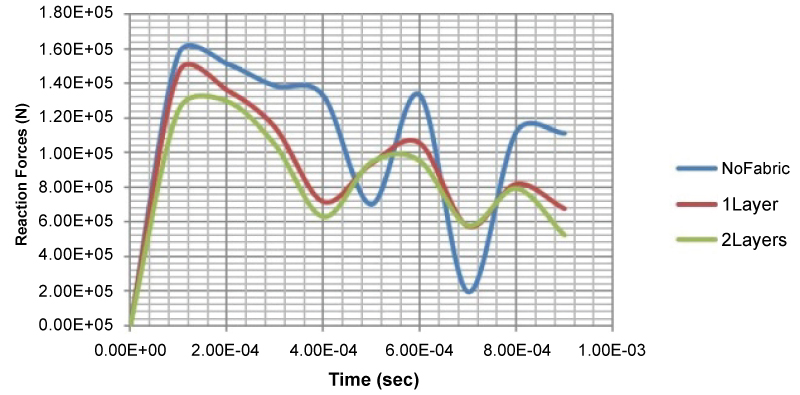
Figure 28: Reaction forces versus time...
Reaction forces versus time diagrams in the case of explosive mass of 3m0.

Figure 29: Von mises stresses (Pa) at the...
Von mises stresses (Pa) at the innegra layers after 1 ms of 3m0 blast loading.
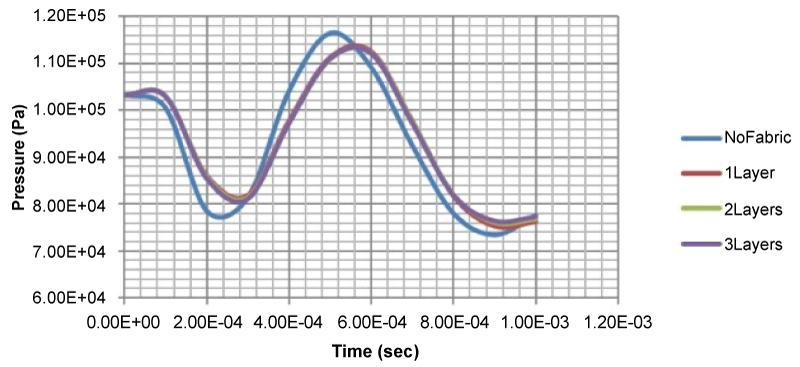
Figure 30: Ambient pressure (Pa)...
Ambient pressure (Pa) versus time (s) diagrams in the case of explosive mass of m0.
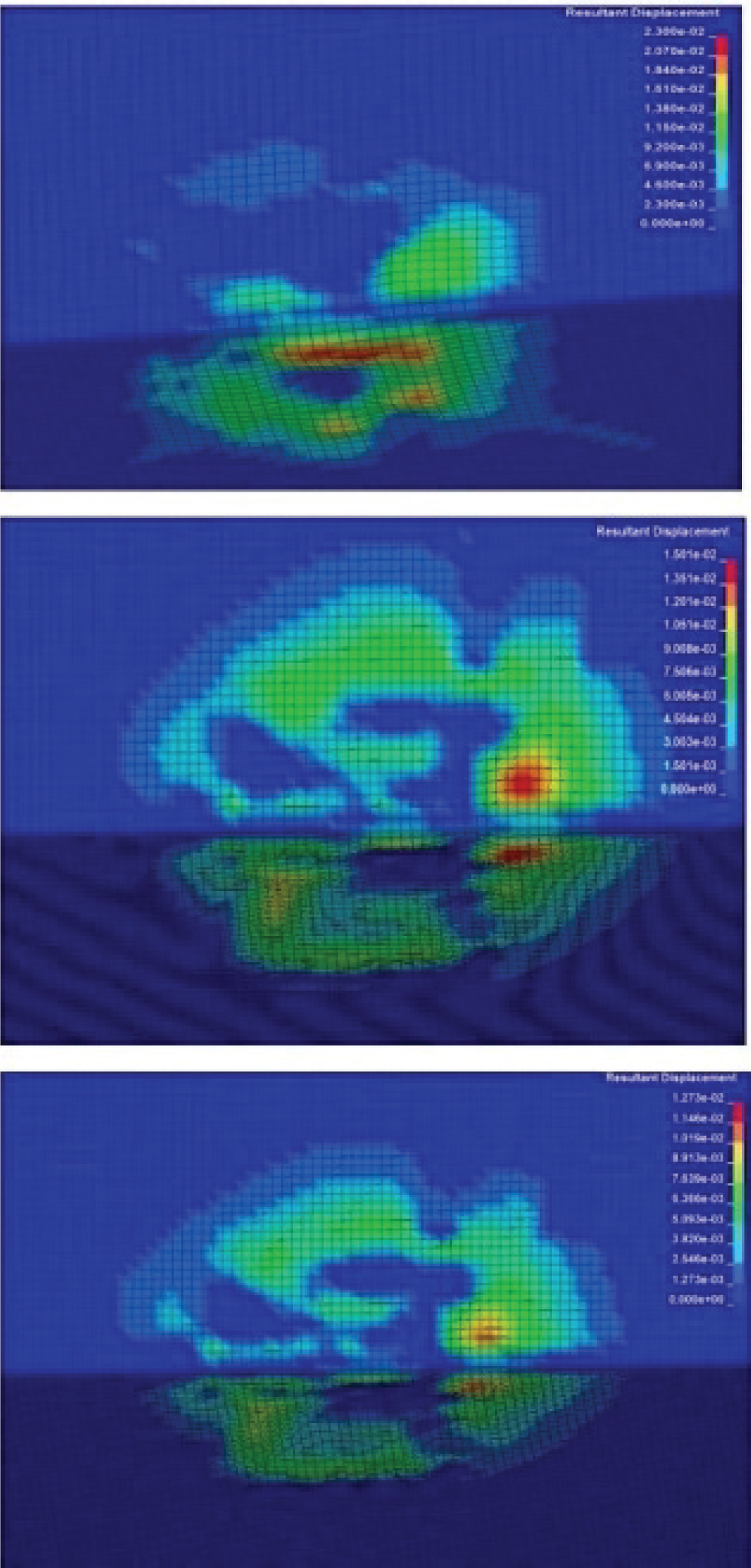
Figure 31: Resultant displacements (m)...
Resultant displacements (m) in the case of the use of 1,2 and 3 layers of innegra fabric outside the ULD for m0 blast loading.
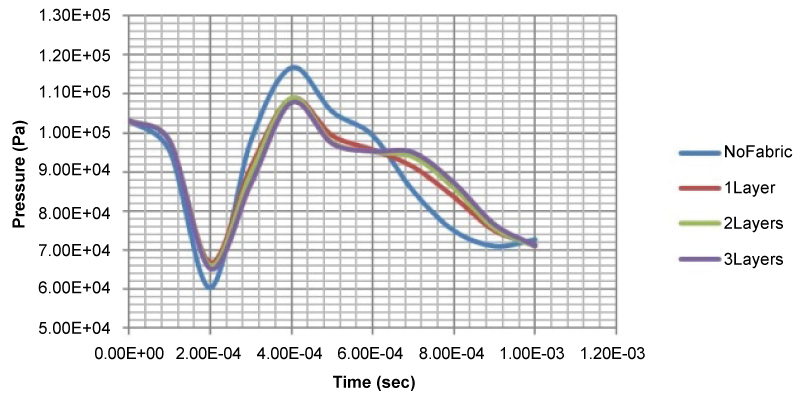
Figure 32: Ambient pressure (Pa) versus...
Ambient pressure (Pa) versus time (s) diagrams in the case of explosive mass of 2m0.
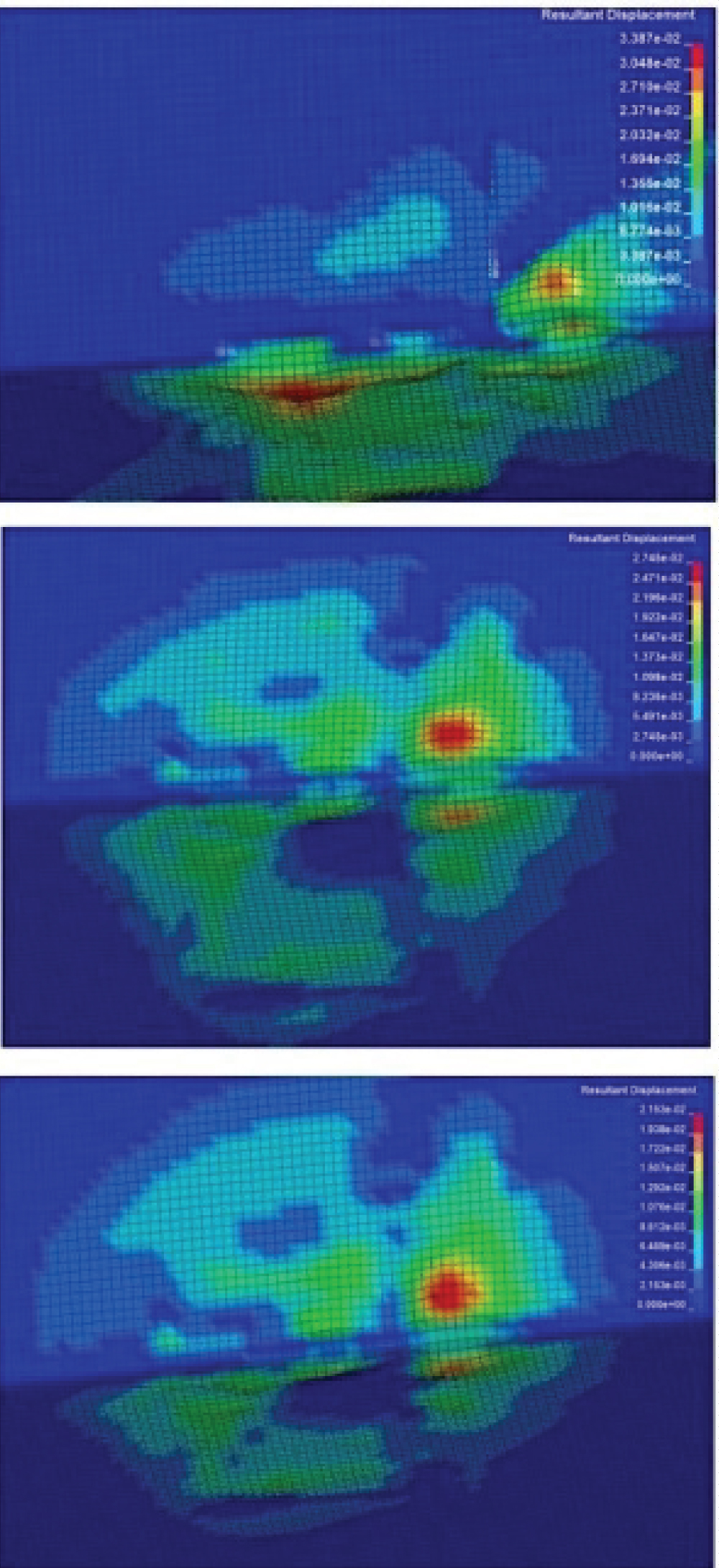
Figure 33: Resultant displacements (m) in...
Resultant displacements (m) in the case of the use of 1,2 and 3 layers of innegra fabric outside the ULD for 2m0 blast loading.
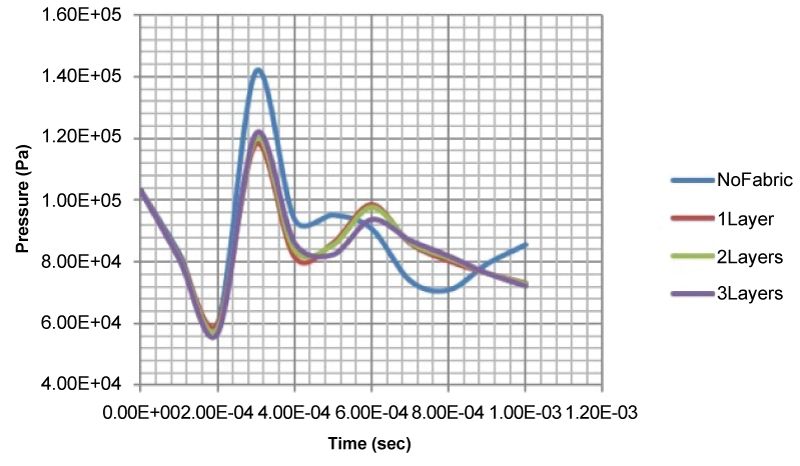
Figure 34: Ambient pressure (Pa) versus...
Ambient pressure (Pa) versus time (s) diagrams in the case of explosive mass of 3m0.
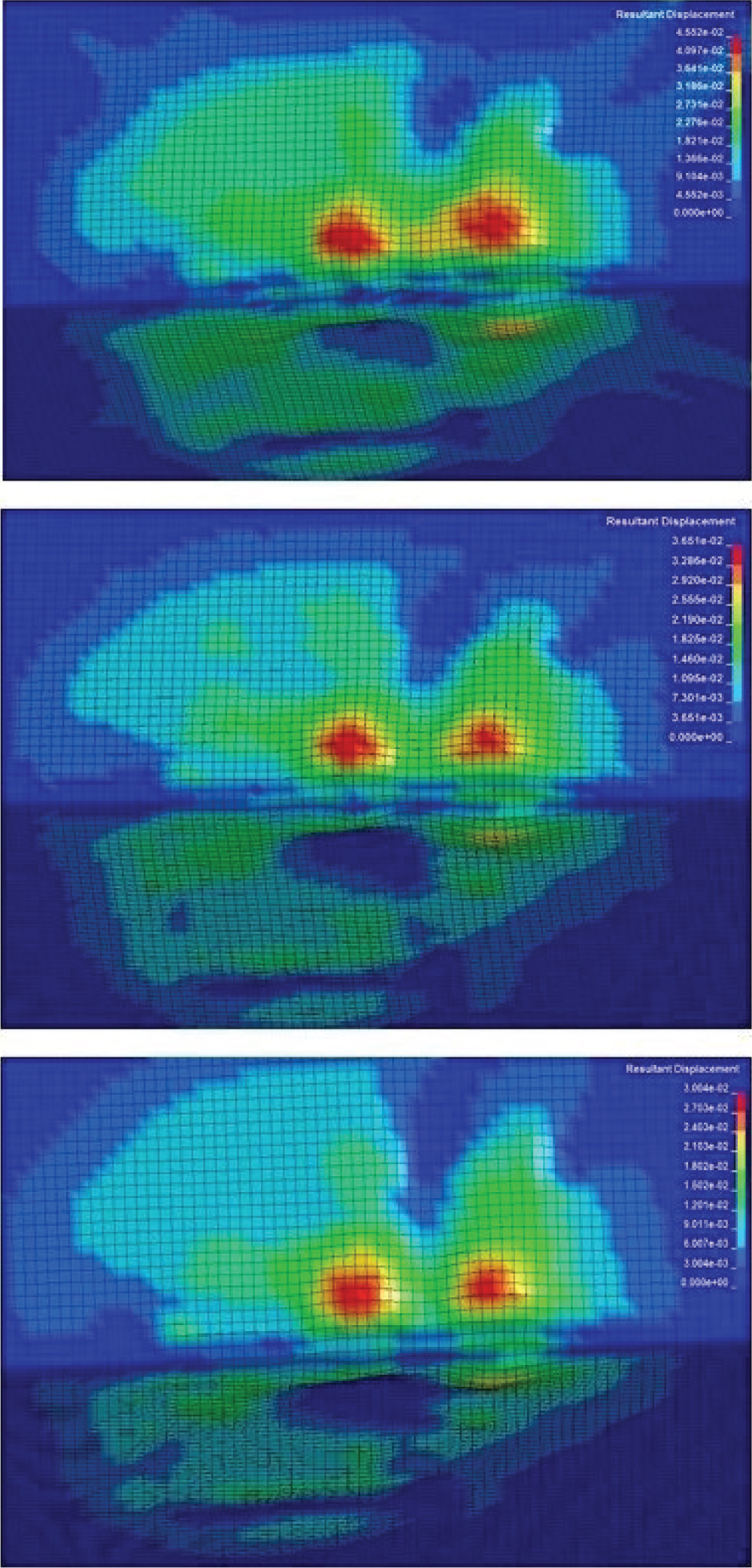
Figure 35: Resultant displacements (m)...
Resultant displacements (m) for 1,2 and 3 layers of innegra.
Tables
Table 1: Material properties of the innegra.
Table 2: Aluminum sheets properties.
Table 3: Frame and luggage material properties.
Table 4: TNT parameters.
Table 5: Air parameters.
Table 6: Maximum pressure values for the blast loading for the internal placement of the fabric.
Table 7: Reaction forces values for the m0 blast loading for the internal placement of the fabric.
Table 8: Pressure values for the m0 blast loading.
References
- www.aerospaceweb.org/question/planes/ q0283.shtml.
- www.fly-bag2.eu.
- Moon YI, Bharatram G, Chimmels Capt SA, Venkayya Dr VB (1996) A vulnerability map of a commercial aircraft, MSC 1996 world user's conference proceedings.
- Moon YI, Bharatram G, Chimmels Capt SA, Venkayya Dr VB (1995) Vulnerability and survivability analysis of aircraft fuselage subjected to internal detonations MSC 1995 world user's conference proceedings.
- T Kotzakolios, DE Vlachos, V Kostopoulos (2011) Blast response of metal composite laminate fuselage structures using finite element modellin. Composite Structures 93: 665-681.
- Xinglai Dang, Philemon C Chan (2006) Design and test of a blast shield for Boeing 737 overhead compartment. Shock and Vibration 13: 629-650.
- Joseph Gatto (1993) Hardened Luggage Container Design Survey.
- Ala Tabiei, Ivelin Ivanov (2001) Computational micro-mechanical model of flexible woven fabric for finite element impact simulation. International Journal for Numerical Methods in Engineering 53: 1259-1276.
- (2013) Livermore Software Technology Corporation (LSTC). Ls-Dyna Keyword User's Manual version R7.0.
- (2011) Federal Aviation Administration, Explicit Finite Element Modeling of Multilayer Composite Fabric for Gas Turbine Engine Containment Systems, Phase III, Part 1: Arizona State University Material Model and numerical Simulations.
- R Santiago, W Cantwell, Marcilio Alves (2013) Impact on thermoplastic fibre-metal laminates: preliminary results and observations. International Symposium on Solid Mechanics.
- Zahra S Tabatabei, Jeffery S Volz A comparison between three different blast methods in LS-Dyna: LBE, MM-ALE, Coupling of LBE and MM-ALE. 12th International LS-Dyna Users Conference.
- Kotzakolios A Blast response of aircraft structures, PhD Thesis.
- N Aquelet, C Seddon, M Souli, M Moatamedi (2010) Initialisation of volume fraction in fluid/structure interaction problem. International Journal of Crashworthiness 237-247.
- Martin Larcher (2007) Simulation of the Effects of an Air Blast Wave.
- A Alia, M Souli (2005) High Explosive simulation using multi-material formulations. Applied Thermal Engineering 26: 1032-1042.
Author Details
S Kilimtzidis, A Kotzakolios and V Kostopoulos*
Department of Mechanical Engineering & Aeronautics, University of Patras, Greece
Corresponding author
V Kostopoulos, Department of Mechanical Engineering & Aeronautics, University of Patras, Greece, Tel: +302610969443, +302610969441, E-mail: [email protected]
Accepted: April 15, 2017 | Published Online: April 17, 2017
Citation: Kilimtzidis S, Kotzakolios A, Kostopoulos V (2017) Blast Reinforcing of Unit Load Device Using High Modulus Polypropylene Plain Weave Fabrics. Int J Astronaut Aeronautical Eng 2:006.
Copyright: © 2017 Kilimtzidis S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The present study investigates whether lightweight fabrics can be used for reinforcing the Unit Load Device (ULD) of a commercial aircraft, protecting them from potential bomb threats or explosives. As a first step, a numerical model of the fabric was developed and introduced to LS-Dyna for modeling a low-velocity impact event and the results were compared against conducted corresponding experiments, in order to validate the fabric properties concluded by the analysis. Having validated the fabric properties, a ULD model is developed and shielded using the considered fabric. The shield is placed initially inside the ULD and was followed by an alternative outside placement. The fabric material was chosen to be Innegra which is a high modulus polypropylene fiber plain weave fabric that offers low weight, excellent levels of impact resistance and damage tolerance. Two scenarios were investigated in the model. The pressure over time curves is the main characteristic used to compare the blast shield's ability. Several other characteristics are compared in order to investigate whether the blast shield is feasible and efficient. The results derived from the numerical simulations indicate that the blast shield becomes significant in higher blast loadings, reducing drastically the induced pressure in the ULD sheets, the ambient pressure outside the structure as well as the magnitude of the reaction forces calculated at the ULD base, mainly via the introduction of energy absorbing mechanisms.
Keywords
Blast hardening, Plain weave fabrics, ULD, Finite element analysis, Fluid structure interaction
Introduction
Over the past decades there have been nearly 86 cases of commercial airliners related to bombings, 53 of them resulting in deaths [1]. There are two main countermeasures to such acts, detection and structural hardening, with detection being the primary one. However, detection of explosives could be rather time consuming and has no guaranteed effects resulting to small yet lethal levels of explosives to escape detection.
The main research studies typically focus on protecting aircraft structures against detonations by either hardening the Unit Load Device (ULD) (Figure 1), a container used to load luggage, freight and mail on aircrafts or the over-head bins, where small quantities of explosives could be stored. The hardening of the ULD has been primarily investigated by the Federal Aviation Administration (FAA) and can provide an onboard countermeasure against bomb threats from the checked luggage. Additionally, within the framework of the EU FP 7 research project under the acronym of FLY-BAG2, the response of the ULD due to blast loading has been investigated making use of high performance, lightweight textile based materials as a passive security measure for the mitigation and containment of onboard blast and for the cost-effective retrofitting of aircraft travelling on critical routes [2].
The Finite Element Analysis regarding the response of aircraft structures to blast loads has been widely investigated over the past years. Moon, et al. [3,4] have developed finite element models of a large section of a commercial aircraft fuselage subjected to internal detonations. However, recent research on the subject focuses on the response of smaller structural elements such as stiffened panels and pressurized skin. The blast response of metal composite laminate fuselage structures using finite element modelling has been investigated by Kotzakolios, et al. [5]. Finite element models of a typical commercial fuselage were generated for two material configurations, aluminum and GLARE. Simulations were performed for different charge locations for both material configurations. The extent and location of damage allowed the generation of a vulnerability index. However, within the framework of the aforementioned study, the ULD structure, typically including the explosive device, has not been taken into consideration during the simulation. X. Dang, et al. [6] demonstrated the feasibility of using a composite blast shield for hardening an overhead bin compartment of a commercial aircraft. Three designs, the basic, thick and thin shields were tested and provided useful data that could lead to the implementation of the blast shield design for hardening overhead compartments against the threat of small explosives. The feasibility of using a Hardened Unit Load Device (HULD) has been investigated by the FAA [7]. Several configurations of the Unit Load Device were tested, making use of various materials such as Fiberglass, Polycarbonates, KEVLAR®, etc. and varying charge weights and locations. However, the financial aspect as well as the manufacture ability of the hardened ULD structure needs to be addressed. The potential use of a blast shield could provide a lighter and more cost-effective solution to the reinforcing of the Unit Load Device and should therefore be investigated.
Previous work indicates that the use of lightweight textiles and light weight fibrous material systems made from tough high strength fibers can provide adequate protection and hence are commonly used in flexible protection systems, such as body armor for military or law enforcement personnel and blast resistant structures. In the last decades, there has been a vast development of new polymeric fibrous materials that exhibit great characteristics such as impact and blast resistance. Some of the most widely used fibrous materials are aramid based (Twaron, Kevlar), ultra-high molecular weight polyethylene based (Spectra, Dyneema) and poly (p-phenylene-2,6-benzobisoxazole) based fibers (Zylon). In the present study, the material used in order to investigate the blast protection offered to a ULD structure is a light weight, high modulus polypropylene plain weave fabric, available under the commercial name of Innegra.
Of particular interest in the present study is the response of a common ULD to blast loading with the addition of a specific lightweight Innegra fabric, in order to reinforce the structure exposed to blast loading and create a blast shield able to protect the ULD as well as the surrounding critical structural aircraft components, such as the frames, the stringers and the fuselage in general. Although it would be ideal to analyze the full-scale coupled aircraft/ULD system under explosive loading, the computational resources needed for such an endeavor are not available, thus we restrict ourselves to the study of the ULD behavior.
Validation of the Fabric Behavior under Impact Loading Experiments
Prior to the main application, it is important to validate the material properties of the Innegraplane weave fabric, which was chosen as the blast shield for the ULD blast loading. A drop testing device was developed in order to experimentally characterize the specific fabric, as shown in (Figure 2). A numerical model was also developed in order to calibrate and validate the material properties. The present study focuses on modeling the drop testing experiment conducted under a low velocity impact, aiming at the validation of the given properties of the fabric under investigation.
For the present analysis, LS-Dyna has been chosen for carrying out transient dynamic simulations of high velocity impacts and blast phenomena.
LS-Dyna material model for fabrics
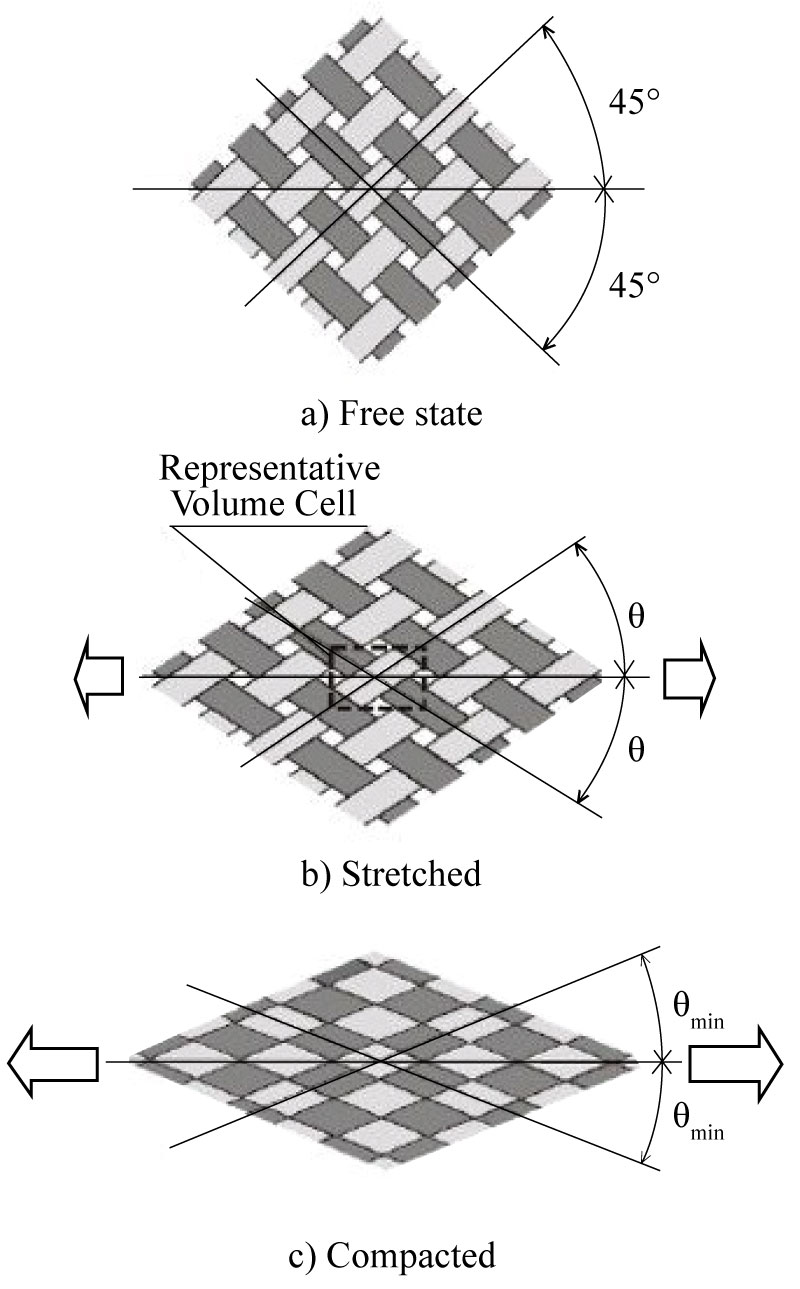
The LS-Dyna material model selected for the simulation of the fabrics behavior is the *MAT_235_Micromechanics_Dry_Fabric. The model developed by Tabiei and Ivanov [8] utilizes the micromechanical approach taking into account of the yarns interaction. The model is based on the Representative Volume Cell (RVC) as it is shown in Figure 3, which represents the periodic structure of the fabric. The RVC is divided into four sub cells taking advantage of the symmetry.
The Representative Volume Cell (RVC) approach is utilized in the micro-mechanical model development. The direction of the yarn in each sub-cell is determined by two angles-the braid angle, θ (the initial braid angle is 45 degrees), and the undulation angle of the yarn, which is different for the fill and warp yarns, βf and βw (the initial undulations are normal few degrees), respectively (Figure 4). The starting point for the homogenization of the material properties is the determination of the yarn stiffness matrices. The elasticity tensor is given in (Figure 5).
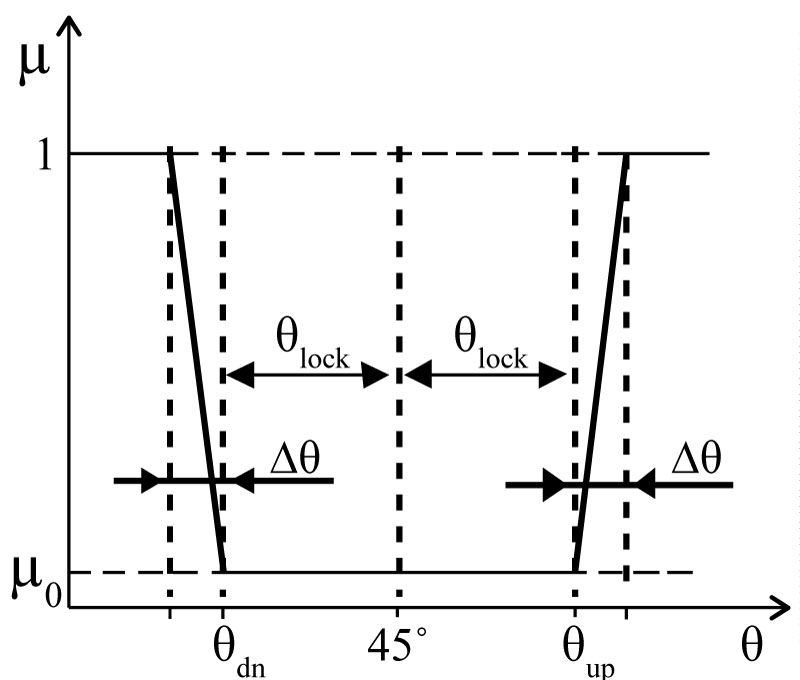
Where E1, E2, ?12, ?23, G12 and G23 are Young's moduli, Poisson's ratio, and the shear moduli of the yarn material, respectively. μ is a discount factor, which is a function of the braid angle, θ, and has a value between μ0 and 1 as shown in (Figure 6). Initially, in free stress state, the discount factor is a small value (DSCF = μ0 << 1) and the material has very small resistance to shear deformation if any.
When the locking occurs, the fabric yarns are packed and they behave like an elastic media as seen in (Figure 7). The micro-mechanical model is developed to account for the reorientation of the yarns up to the locking angle. The locking angle, θlock, can be obtained from the yarn width and the spacing parameter of the fabric using simple geometrical relationship. The transition range, Δθ (angle tolerance for locking), can be chosen as small as possible, but big enough to prevent high frequency oscillations in transition to compacted state and depends on the range to the locking angle and the dynamics of the simulated problem.
Stress calculation and failure
In case of plane stress for shell element applications in the explicit finite element codes, the transverse strain increment component, Δε3, has to be calculated first. This transverse strain is used in calculating the thickness change of the shell elements. The transverse strain is obtained from the condition Δσ3 = 0 as follows:
Where Cij are the RVC stiffness matrix components.
Note that components Ci5 and Ci6 for i-1,2,3,4 are always 0 because of (30) and the stiffness matrix is symmetric.
The stress at the integration point of the shell element is calculated for n+1 time step as follows:
The calculated stress is used for the calculation of the element internal forces. The calculation is simplified in the case for membrane shell element application, because Δε5 = Δε6 = 0. To find the stress in yarns, the stress and strain increment vectors of RVC have to be split in iso-strain and iso-stress components and the unknown part of stress increment components, {Δσn}k , is calculated for each sub-cell in RVC co-ordinate system. Then the stress increment vector of each sub-cell is transformed to the material co-ordinate system by the partitioned transformation matrix of the sub-cell:
Where the stress is increment of k-sub-cell on the xyz-co-ordinate system and is the stress increment of the k-yarn in its material co-ordinate system. The accumulated yarn stress is calculated fir the n+1 time step as follows:
The maximum stress failure criterion for the yarn is then applied, σ1 > ?t , where Xt is the ultimate strength at failure.
The initial mechanical properties of the Innegrafabric, which also act as an input for the material model used in LS-Dyna, are listed in (Table 1):
Numerical modeling of the low-velocity impact
The numerical model of the impact test has been realized taking into account all relevant parts of the experimental test according to (Figure 2). The dart and the flanges have been modeled as rigid materials due to the stiffness mismatch between the parts (i.e. the dart and the flanges with the fabric). The flanges are constrained in the zy plane and in the x-direction with an additional clamping device. Both were modeled using solid elements. The fabric was modeled using shell (QUAD4) elements, with a thickness of 0.5 mm, fully integrated in order to eliminate hourglass modes.
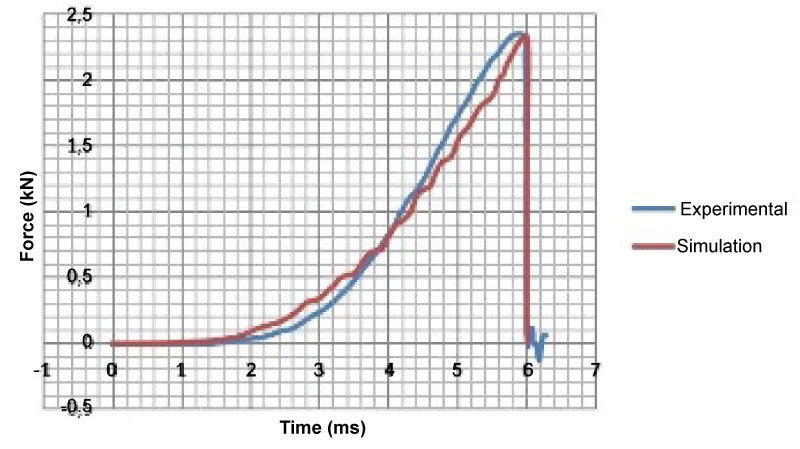
The initial velocity is assigned to the dart, taking into account the energy of the test to be simulated, which in our case was 15 J, resulting to a velocity of 3.83 m/s. The constraints applied to the dart allow only displacements in the x-direction. The mass of the dart was modeled as a concentrated mass on top of the dart equal to 2.045 kg via the Element Mass element. The numerical model created can be seen at (Figure 8). The calibration of the material model will be focused on the Force (F) over time (s) curve of the impact, acquired by the piezoelectric dart and compared with the numerical results.
As far as the other parameters needed for the implementation of the model, the following assumptions have been made [9,10]: an automatic penalty contact algorithm (*Contact_Automatic_Surface_to_Surface) was chosen due to its capability to handle different size of elements that come into contact and its relatively fast completion times. There was also a dynamic and static friction coefficient considered between the dart and the fabric equal to 0.1, in order to avoid noise problems. To avoid unstable vibrations due to the contact between materials of fairly low stiffness, the viscous damping coefficient was considered into the model, so as to annihilate such vibrations. Finally, due to the stiffness mismatch issue as stated earlier, the way the contact stiffness was calculated also changed by picking the SOFT option and hence removing the stiffnesses of the members in contact terms from the calculations.
Results
In Figure 9 the evolution of the failure of the fabric during the impact with the dart is reported.
The force versus time curve can be obtained by either using LS-Dyna history of variables, thus plotting the force upon the contact interface for the duration of the impact, or by plotting the recorded acceleration of the nodes of the dart and multiplying them with its mass, resulting to the applied force. Both ways resulted to the same force versus time curve. The force (N) versus time (s) curve of the 15 J drop is reported in (Figure 10). The comparison of the results of experimental test against the simulation ones shows the level of confidence and reliability of the material model developed. In order to match the experimental force-time curve of the low-velocity impact the material properties of Innegra fabric were calibrated. The initial values of the transverse shear modulus of the Innegra and the strain to failure were changed in order to obtain a close approximation between the numerical model and the experimental data. In particular, the transverse shear modulus of the fabric layer (TRS) was changed from an initial value of 0.1 GPa to 1GPa and the strain to failure, Xt, from an initial value of 6.5% to 11.8%.
Blast Loading of a ULD
Having validated the Innegrafabric numerical model, we proceed to the aim of this study, which involves the blast loading response of a specific ULD structure and the application of Innegra fabrics, either internally or externally, in order to investigate their effect in the direction of a blast shield of the structure. The ULD chosen for this application is one widely used in modern aircrafts, and specifically the ULD-LD3, shown in (Figure11).Within the frame of the present study, the blast shielding concept based on Innegra fabrics was used for the investigation of the response of the ULD structure to blast loading. The load transfer from the ULD to the aircraft structure was not investigated in this paper. The explosive used for this application is TNT of mass m0, placed inside a luggage and the charge weight varies up to 3m0 quantities, which will be denoted as m0, 2m0, 3m0 and correspond to two and three times the initial charge weight m0, respectively. The two primary response quantities used for comparing the simulation results is the pressure over time outside and inside the structure as well as the resultant force of the reaction forces of the fixed base.
The nodes of the base are supposed to be fixed as seen in Figure 12 and the resultant reaction force of these nodes are printed for each scenario in the SPC_FORC file available in LS-Dyna.
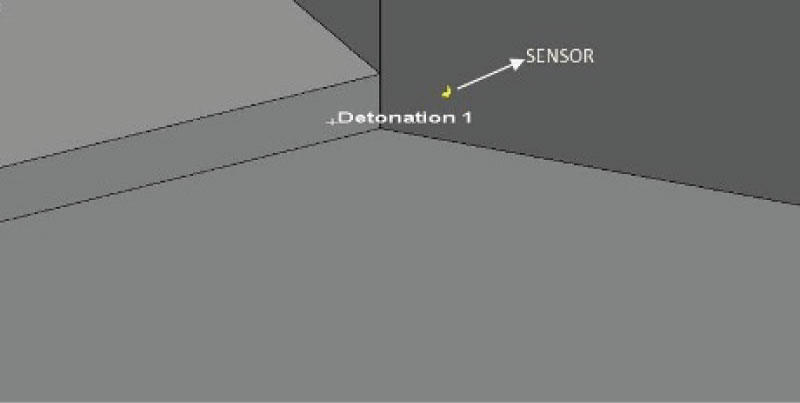
As far as the pressure measurements concerned, a sensor is attached to the structure in the vicinity of the explosive, able to measure the induced pressure, as seen in Figure 13, where the detonation point is also visible.
Modeling parameters of the ULD
The ULD was modeled using beam elements for the frame and shell elements for the aluminum faces, as seen in Figure 11, in order to have compatible degrees of freedom for the elements in contact. The ULD faces were assumed to be made of Aluminum 2024-T3 with a wall thickness of 2.5 mm. The material model used for the aluminum faces is the ???098_Simplified_Johnson _Cook of LS-Dyna, which is widely used in cases where the strain rates vary over a large range. The input properties are shown in (Table 2) [11]. The frame was assumed to be made of Aluminum 2024-T6, a common aluminum used in aircraft applications. The frame was modeled using the MAT 024_Piecewise_Linear_Plasticity material model of LS-Dyna, an elastic-plastic material. Its properties are reported in (Table 3). As far as the luggage concerned, an ABS (Acrylonitrile butadiene styrene) material was chosen and it was modeled with shell elements making use again of the MAT024_Piecewise_Linear_Plasticity material model with its input properties shown in (Table 3 and Figure 14).
Explosion modeling
In order to simulate the explosion detonation and its interaction with the ULD structure, numerical methods that can handle problems including interaction between solid and fluid domain are needed. These problems are treated using special tools referred to as Hydrocodes. Hydrocodes are computational continuum mechanics tools able to simulate the response of both solid and fluid materials under highly dynamic conditions, such as explosion and impact, where shock wave propagation is a dominant phenomenon. The most common method used for these applications is the ALE (Arbitrary Lagrangian Eulerian) approach, where the fluid-structure interaction is handled by a coupling algorithm. The background air mesh configuration consists of two materials, the air and the explosive (TNT). The *ALE_MULTI_MATERIAL_GROUP card defines the two materials in LS-Dyna. The explosive is defined using *Mat_High_Explosive_Burn, which controls the explosive's detonation characteristics. For the TNT, a Jones_Wilkins_Lee(JWL) equation of state (EOS) is used. The JWL EOS defines the pressure as a function of the relative volume, V, and initial energy per initial volume, Eint, such that
The parameters A, B, R1, R2 are constants pertaining to the explosive and reported in (Table 4) [12,13]. The *Initial_Volume_Fraction_Geometry card defines the initial distribution of air and TNT [14]. It also defines its initial shape and place. The card *Initial_Detonation defines where and when the detonation starts.
The material model corresponding to the air domain is Mat_Null, where the pressure used is given by:
Where C0,C1, C2, C3, C4, C5 and C6 are constants and with the ratio of current density to initial density. Eint is the internal energy per unit initial volume. For gases, which the gamma law equation of states applies such as air, the above equation reduces to with the ratio of specific heats. All the used parameters for this method are given in (Table 5) [15,16]. A monotonic, second order accurate Van-Leer advection scheme is used. In order to couple the air domain to the structure we use the *Constrained_Lagrange_to_solid card.
Rivets modeling
As seen in Figure 11, where a typical ULD is shown, rivets are used to hold the frame and Aluminum faces together. The number of rivets used is approximately 13 per sheet side. In order to model the rivets we use a tiebreak contact in LS-Dyna and particularly *Tie break_Nodes_to_Surface, a contact algorithm that ties the nearby nodes. This contact remains until the failure criterion implemented by the algorithm is fulfilled. The criterion states that failure occurs whenever:
Here fn, fs are the normal and shear interface force, NFLF and SFLF are the normal failure force and shear failure force respectively and NEN, MES are the exponents for normal and shear forces, both equal to 2. The tensile strength, NFLF is calculated via the following equation:
Where Fbr is the ultimate allowable stress, d the rivet diameter and t the sheet thickness. Fbr = 427 MPa, d = 3 mm and t = 2.5 mm, which results to NFLF = 3.2 kN
The shear strength, SFLF is calculated as:
Where Fsu is the ultimate allowable stress, d the rivet diameter and t the sheet thickness. Fsu = 283 MPa, d = 3 mm and t = 2.5 mm, which results to SFLF = 2.4 kN
The above values are multiplied by a safety factor for the number of rivets, equal to the number of rivets per sheet (assumed to be 13), divided by the number of nodes tied via the contact algorithm per sheet (7 per sheet), therefore the safety factor is 1.86. Hence, the final tensile and shear force values at failure for the rivets are:
NFLF = 6 kN and SFLF = 4.5 kN
Blast loading of the ULD
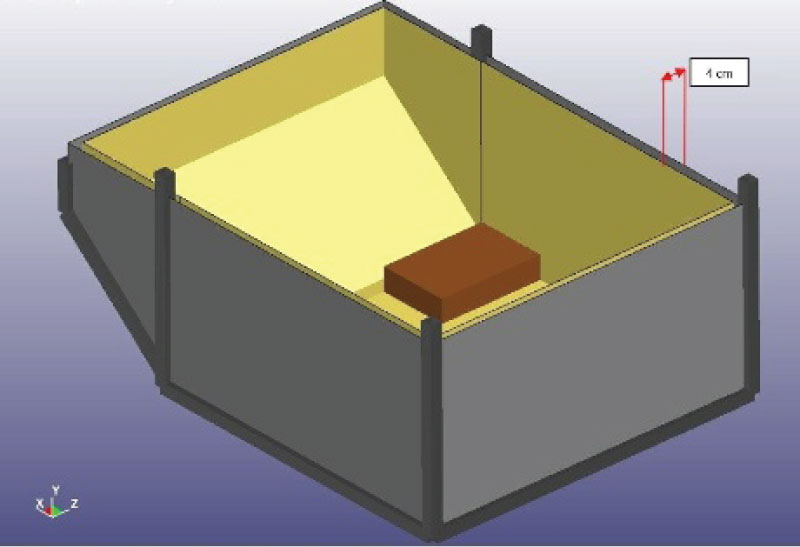
As stated earlier, the ULD will be initially loaded without applying any blast shield. This is the reference blast loading scenario, and pressure versus time and reaction forces versus time plots are calculated. This loading scenario involves blast loading with the minimum quantity of the explosive, denoted as m0. The concluded results will be compared against the results concluded in the case of using Innegrafabric layers, which are placed inside the structure. The fabric layers are connected closely to the ULD structure via the *Tied_Surface_to_Surface_Offset contact algorithm provided in LS-Dyna, as seen in (Figure15).The distance between the fabric and the ULD sheets is 4 cm, as seen also in Figure 15. One and two Innegra fabric layers have been used to that direction. The fabrics are modelled using shell (QUAD4) elements, with a thickness of 0.5 mm, fully integrated in order to eliminate hourglass modes, as described in Section 2.2.
Reference m0 mass of explosive used for blast loading
The lowest amount of TNT for this study induced small plastic deformations closed to the blast region, as seen in Figure 16, where the Von Mises stresses in units of Pa of the ULD, at the time of 0.1 msec after the blast, are shown. The rivets in the vicinity of the detonation have also failed, since satisfying the failure criterion as stated in section 3.3.
The modelling for the addition of the Innegra layers is completed by the addition of a contact algorithm between the layers and particularly the contact *Tiebreak_nodes_to_Surface.
With the addition of one layer of Innegra fabric inside the structure, the Von Mises stresses at the aluminum faces are lower; however, the small plastic deformation of the aluminum faces close to the explosive region remain. The Innegra layer undergoes also plastic deformation and local failure, as seen in (Figure17).
Adding internally a second Innegrafabric layer, Innegra layers appear the same failure mode and plastic deformations, as seen in (Figure 18). However, increased Von Misses stresses on aluminum faces are also recorded in this case, which might occur due to the increased stiffness of the fabric resulting in higher frequency vibrations, which for the particular blast loading induce a higher stress field of the ULD structure.
The pressure on the aluminum faces, near the explosive source versus time is reported in (Figure 19). The addition of one Innegra layer reduces the experienced pressure of the aluminum face by 6%, while the addition of a second layer has a negative effect, resulted to a pressure increase, which can be explained by the increased stiffness of the fabric which induces higher frequency vibrations for this scenario. Additionally, the introduced damage absorbing mechanisms by the fabric reduce the kinetic energy of the incident pressure wave and delay the arrival time of the peak pressure as seen below.
The maximum pressure values induced at the aluminum faces of the ULD, obtained by the sensor as depicted in Figure 13 versus the number of Innegra layers for the case of m0 blast loading are reported in (Table 6).
The reaction forces over time, calculated at the point where the sensor has been placed as shown in Figure 12, are also reported in (Figure 20). The addition of the Innegra layer decreases the reaction forces by nearly 36%. However, the second layer has no significant effect, decreasing the reaction forces by an additional 0.5%.
The addition of the Innegra fabric has an overall positive impact on the reduction of the resultant reaction force. Specifically, as seen above the amplitude of the induced vibration of the structure in drastically decreased. Furthermore, the Innegra fabric induces a more stable almost sinusoidal vibration with lower amplitude, due to the ability of the fabric to transform the incident kinetic energy of the pressure wave into strain energy of the yarns, thus introducing energy absorbing mechanisms. The reaction forces with the presence of Innegra layers are reported in (Table 7).
2m0 mass of explosive used for blast loading
The 2m0 TNT mass of explosive used for blast loading induces greater plastic deformations at the ULD aluminum faces, as seen in (Figure 21). The side panel is slightly detached from the ULD structure.
With the addition of one layer of the Innegra fabric inside the structure, the Von Mises stresses are decreased; however, the plastic deformations remain. The Innegra layer undergoes plastic deformation and final failure, which appears to be at a larger area compared with the former case of m0 used mass of explosive, as it was expected and can be seen in (Figure 17 and Figure 22).
The introduction of the second Innegra layer lowers further the Von Mises stresses on the ULD faces. Also in this case, as it was expected, both Innegra layers failed as seen in (Figure 23). In contrast to what reported in the case of TNT mass of m0 blast loading, where the Von Mises were greater with the addition of the second layer, this phenomenon is not observed for this case.
The pressure versus time diagrams is also given in (Figure 24). In this case, the introduction of an Innegra layer has a significant effect on the monitored pressure values, which drops considerably. However, the introduction of the second Innegra layer still has no considerable effect on the monitored pressure. The delay at the time of arrival of the peak pressure is not observed in the present case due to the fact that the fabric layers are close to the detonation point, which results in almost instantaneous failure of the fabric.
The maximum pressure values versus innegra layers for the case of 2m0 blast loading are reported in (Table 6).
The reaction forces versus time are also reported (Figure 25). In the case of 2m0 mass of explosive used for blast loading, the curves are very similar to each other, smoother and their amplitude is higher (more than 3 times the relative amplitude calculated when m0 explosive mass were used) as it was expected. The reaction forces lower slightly their values with the addition of the Innegra layers.
The reaction force values over Innegra layers are reported in (Table 7).
3m0 mass of explosive used for blast loading
The highest amount of explosive charge concludes to the highest plastic deformations of the aluminum faces of ULD, as it was expected and can be seen in (Figure 26). The rivets in the vicinity of the detonation have also failed as in the case of 2m0 blast loading, but at a higher extent. The introduction of the Innegra layers to the ULD, although reduce the pressure experienced by the aluminum faces (Figure 27), do not reduce significantly the reaction forces (Figure 28). The Innegra layers also in this case undergo plastic deformation and a more extensive failure area, compared to the other blast loading cases, studied earlier, as it is shown in (Figure 26).
More specifically, the introduction of the second Innegra layer lowers even further the Von Mises stresses in the ULD due to the increased stiffness and reduced permeability of the fabric (Figure 29).
The pressure experienced by the sensor placed over the aluminum face shows a considerable increase compared to the monitored values in the case of lower mass of explosive. The addition of the first Innegra layer decreases drastically the peak pressure, nearly to 52%. The introduction of the second layer has an additional positive effect on the pressure decrease, although this decrease is limited.
The maximum pressure (Pa) values versus Innegra layers for the case of 3m0 blast loading are reported in (Table 6).
The reaction forces versus time plots in the case of explosive mass of 3m0 are shown in (Figure 28). The maximum values of the reaction forces versus the number of Innegra layers are given in (Table 7).
External placement of the innegra hardening layers
In this case, the Innegra fabric are placed outside the ULD, in a way to envelop the ULD in order to minimize the ambient pressure wave that could have fatal consequences and/or to be used as a fragment shield that prevents the blast resulted fragments from spreading. At these scenarios, the analysis focused on the external pressure versus time as well as the resultant displacements of the Innegra fabrics. The number of layers varies this time from 1 to 3. The resultant reaction force of the fixed base is not presented due to the fact that the fabric was placed far from the base and so no particular effects on the reaction forces are expected. In all the cases discussed below, the resulted ambient pressure outside the shielded ULD, closed to the side of explosive detonation, and the integrity of the Innegra 'envelop' are discussed.
Reference m0 mass of explosive used for blast loading
In this case the 'ambient pressure 'versus time plots are given in (Figure 30). It is important to mention here that an initial pressure drop is followed by an increase pressure field. The addition of the first Innegra layer reduces the amplitude of both under-pressure and pressure wave outside the ULD close to 5% and delays the arrival of the pressure wave. The increase of the number of Innegra layers does not provide any further positive effect as clearly showed in (Figure 30).
The maximum pressure values versus the number of the used Innegra layers are reported in (Table 8).
The resultant displacements in units of m of the Innegra fabric, at the time the maximum pressure value appears, are presented in (Figure 31). The maximum displacement values indicate the position of the luggage area where the explosive detonation took place. There is no failure reported for the Innegra 'envelop' used.
2m0 mass of explosive used for blast loading
The use of 2m0 mass of explosive for the blast loading of the ULD structure as it was expected leads to higher values of both under-pressure and pressure outside the ULD at the point of measurement. The addition of the first Innegra fabric layer in the way to envelop the ULD structure reduces the amplitude of both under-pressure and pressure wave outside the ULD close to close to 7% and slightly delays the arrival of the pressure wave. The increase of the number of Innegra layers does not provide any further positive effect as clearly showed in (Figure 32).
The maximum pressure values versus the number of the used Innegra layers in this particular case are reported in (Table 8).
The resultant displacements of the Innegra fabric, at the time the maximum pressure value appears, are presented in (Figure 33). The maximum displacement values indicate again the position of the luggage area where the explosive detonation took place. There is no failure reported for the Innegra 'envelop' used.
3m0 mass of explosive used for blast loading
The use of 3m0 mass of explosive for the blast loading of the ULD structure as it was expected leads to higher values of both under-pressure and pressure outside the ULD at the point of measurement. The addition of the first Innegra fabric layer in the way to envelop the ULD structure reduces the amplitude of the pressure wave close to 16%, while leaves almost unaffected the amplitude of the under-pressure wave. The time of arrival of the pressure wave is almost the same for all the studied cases. The increase of the number of Innegra layers slightly variate the positive effect of the Innegra fabric envelop of the ULD structure as clearly showed in (Figure 34). The mitigation of the pressure for the 3m0 blast loading is greater than the 2m0 and m0 blast loading scenarios.
The maximum pressure values versus the number of the used Innegra layers in the case of 3m0 blast loading are reported in (Table 8).
The resultant displacements of the Innegra fabric, at the time the maximum pressure value appears, are presented in (Figure 35). There is no failure reported for the Innegra 'envelop' used.
Conclusions
The possibility of using lightweight fabrics for blast protection of the Unit Load Device (ULD) used in aircrafts has been considered. The material properties of the lightweight fabric used as a blast shield were validated and altered according to a low-velocity impact experiment. The blast shield, initially placed inside the structure, showed insignificant pressure reduction for the m0 TNT loading and even an increase of the internal pressure for the two-layered fabric. Moving onto higher blast loads, i.e. 2m0 and 3m0, the importance of the blast shield becomes even more considerable. The one-layered shield was able to reduce the peak pressure up to 50% for the 3m0 case and 24.5% for the 2m0 loading. The addition of a second layer to the fabric had marginal impact on the pressure reduction for the m0 and 2m0cases. As far as the reaction forces are concerned, a drastic decrease of the reaction forces is observed. The amplitude of the curves reduces and the resulting motion is almost of a sinusoidal type. For all the cases, the fabrics inside the structure failed. The introduction of the energy absorbing mechanisms due to the fabric enable the transformation of the kinetic energy of the blast wave into strain energy of the yarns, decreasing this way the damage induced to the structure. The addition of Innegra layers increased the stiffness and reduced the permeability of the fabric thus decreasing the induced stresses on the ULD. For the scenario of the external placement of the fabrics, the fabric layers do not fail. Similarly, to the first scenario, there are no differences between the external pressures for the m0 case. However, the addition of one layer of fabric is capable of decreasing the external pressure drastically. The further addition of Innegra layers do not further contribute to a decrease in pressure. As far as the usage of the blast shield in a real aircraft concerned, a plethora of experiments for varying blast loadings and fabric configurations need to be conducted in order to determine whether the blast can be safely contained, making sure also that the numerical models developed are valid. Additionally, coupled fuselage/ULD models should be developed in order to predict the response of the system under a blast scenario.
Acknowledgements
The authors acknowledge the support of the present work by the EU FP7 Transport (including Aeronautics) L1 project 'Advanced technologies for bomb-proof cargo containers and blast containment units for the retrofitting of passenger airplanes' (FLY BAG2).