
International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 2, Issue 1
Research Article
DOI: 10.35840/2631-5009/7503
Preliminary Design of a Generalized Vestibular Sensory System
Hooshang Hemami1 and Kamran Barin2*
Table of Content
Figures
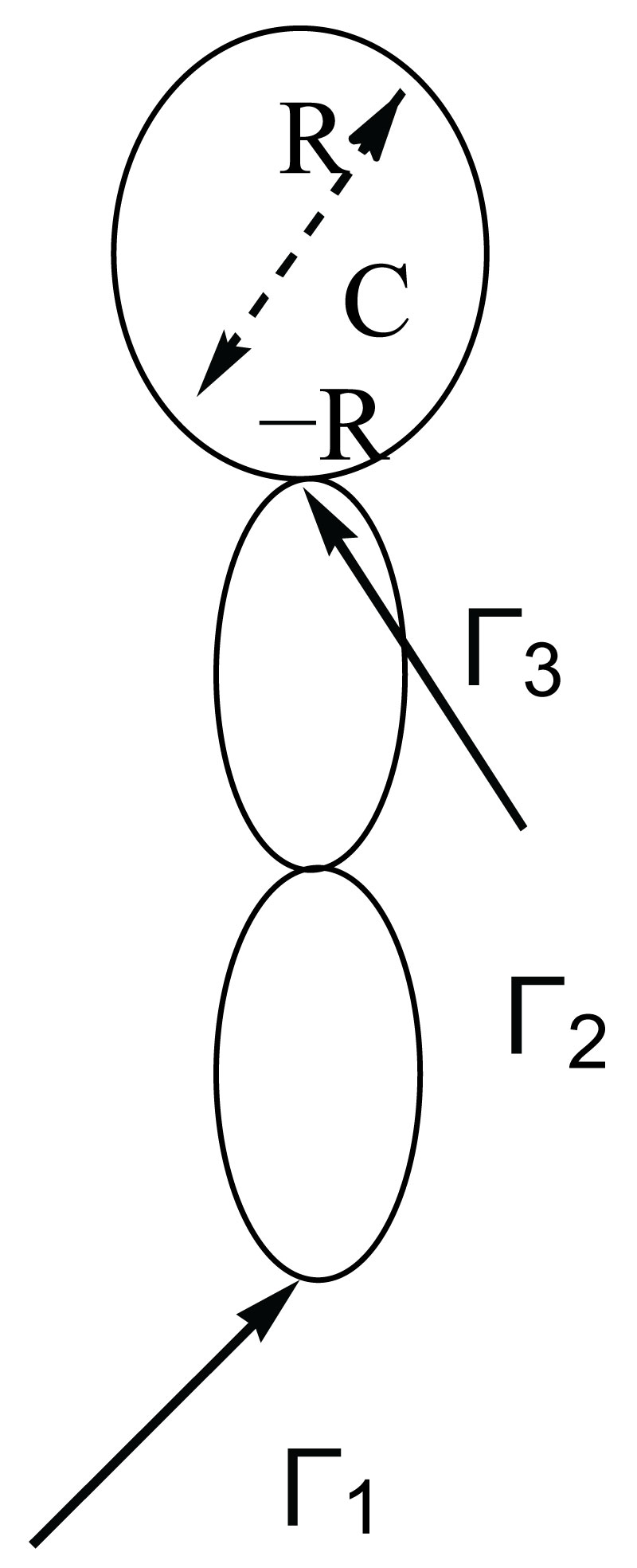
Figure 1: The three-segment head and neck with three-dimensional accelerometers...
The three-segment head and neck with three-dimensional accelerometers at Ql and Qr corresponding to approximate locations of the semi-circular canals in the head (at vectors R and -R in BCS). Γi for i = 1,2,3 is the joint force, expressed here in the ICS, but measured by the proprioceptive sensory system.
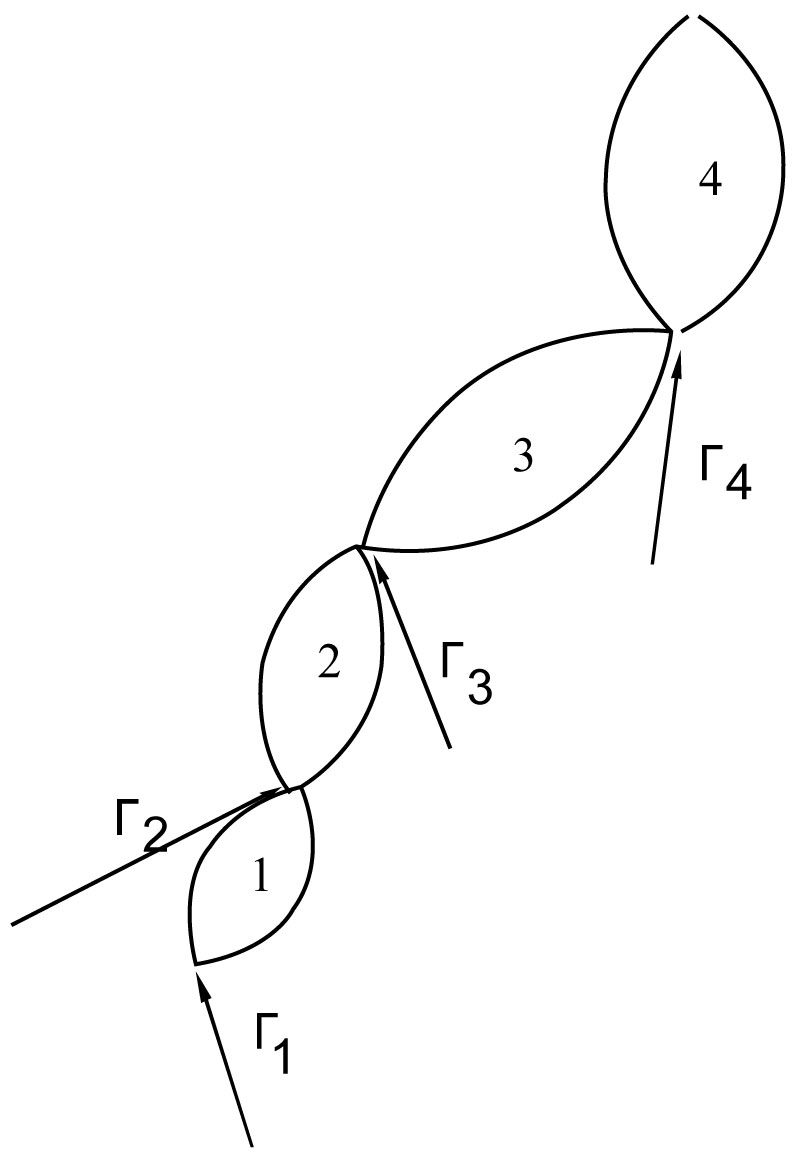
Figure 2: The four-rigid-body system with joint forces Γ1, Γ2, Γ3 and Γ4...
The four-rigid-body system with joint forces Γ1, Γ2, Γ3 and Γ4. The toes support the biped and are at the origin of the inertial coordinate system: the x axis is to the front, the y axis is to the left, and the z axis is vertically upward.

Figure 3: The four sagittal Bryant angles (in rad.) and angular velocities...
The four sagittal Bryant angles (in rad.) and angular velocities (in rad./s) as functions of time. The system is driven to the vertical stance.
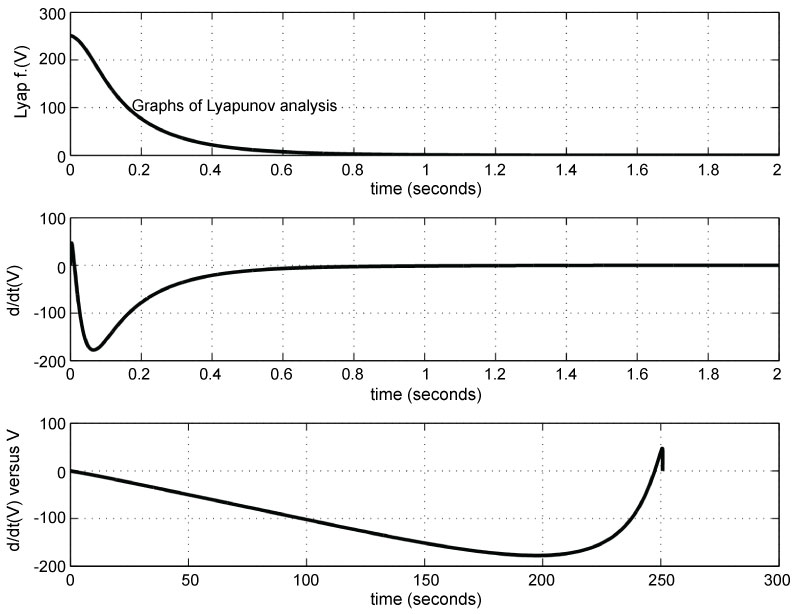
Figure 4: The Lyapunov function V, ∂V/∂(t) and the phase plane...
The Lyapunov function V, ∂V/∂(t) and the phase plane trajectory of V are shown for the transient postural stability. The vertical units are joules and joules/s.
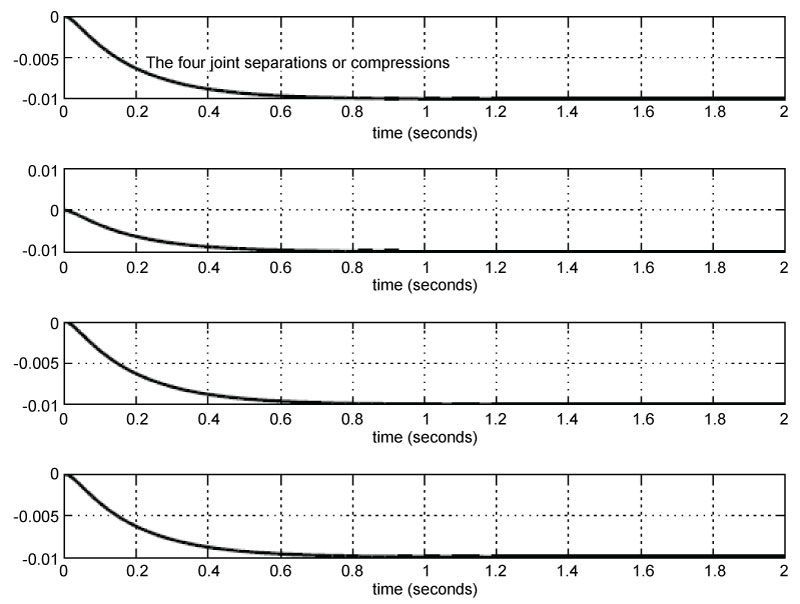
Figure 5: The vertical cartilage compression (in m) at the four joints as ...
The vertical cartilage compression (in m) at the four joints as the weight of the body is gradually borne by the passive structure.

Figure 6: The four velocities of the compression at the four joints (in m/sec)...
The four velocities of the compression at the four joints (in m/sec) as functions of time.
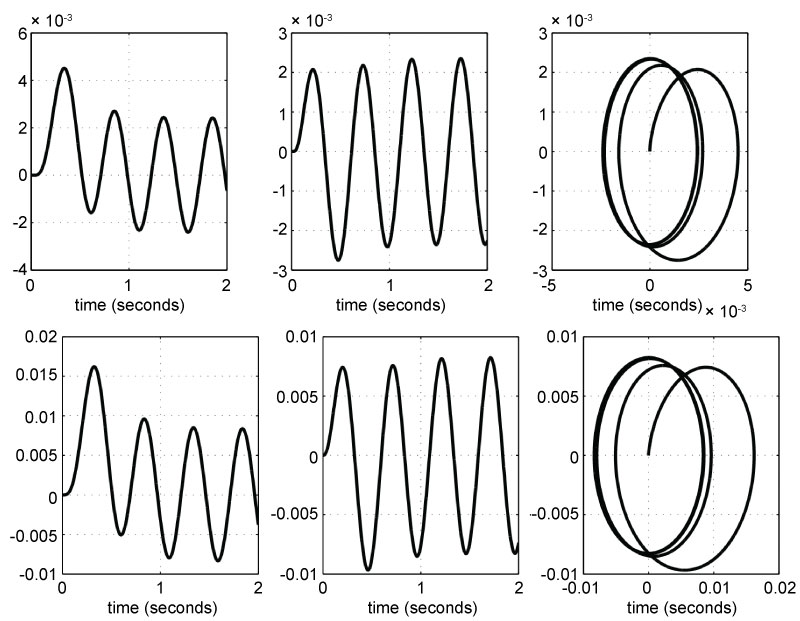
Figure 7: The trajectories of the centers of gravity of the foot (top row)...
The trajectories of the centers of gravity of the foot (top row) and the leg (bottom row). The motion of the centers of gravity in the inertial x-y planes are also shown. All quantities are in meters.
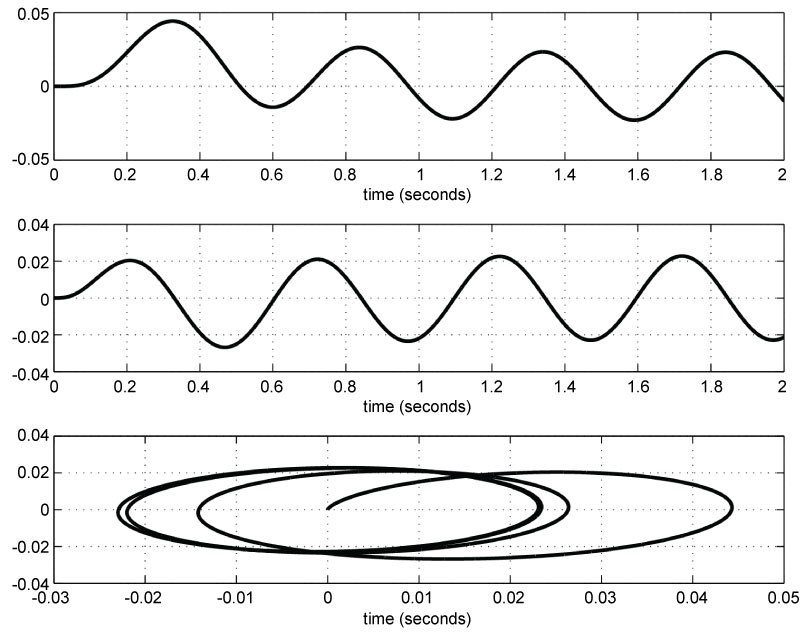
Figure 8: The trajectories of the centers of gravity of the torso and the...
The trajectories of the centers of gravity of the torso and the spatial motion in the x-y plane, all in meters.
References
- S Ramat, D Pre, G Magenes (2006) An inertial model of self-motion based on inertial signals. Conf Proc IEEE Eng Med Biol Soc 28: 4961-4964.
- NS Valentin, KN Hagerman, C Dai, C Della Santina, GY Fridman (2013) Development of a multichannel vestibular prosthesis prototype by modification of a commercially available cochlear implant. IEEE Trans Neural Syst Rehabil Eng 21: 830-839.
- F Bagala, J Klenk, A Capello, L Chiari, C Becker, et al. (2013) Quantitative description of a lie-to-sit-to-stand-to-walk transfer by a single body fixed sensor. IEEE Trans Neural Syst Rehabil Eng 21: 624-633.
- T Anastasio (1995) Vestibuo-ocular reflex. In: M Arbib, The Handbook of Brain Theory and Neural Networks. The MIT Press,1003-1005.
- K Barin, J Durrant (2000) Applied physiology of the vestibular system. In: R Canalis, P Lambert, The Ear: Comprehensive Otology. Lippincott Williams and Wilkins, 113-140.
- RW Baloh, V Honrubia (1990) Clinical Neurophysiology of the Vestibular System. In: FA Davis Company, (2nd edn), Philadelphia.
- V Dietz, M Trippel, G Horstmann (1991) Significance of proprioceptive and vestibulo-spinal reflexes in the control of stance and gait. In: AE Patla, Adaptability of Human Gait, Implications for the Control of Locomotion. North Holland, 37-52.
- D Wang (1991) Parallel Implementation of Multibody Dynamics for Real-Time Simulation. University of British Columbia.
- MG Pandy, F Anderson, D Hull (1992) A parameter optimization approach for the optimal control of large scale musculoskeletal systems. J Biomech Eng 4: 450-460.
- F Anderson, MG Pandy (2001) Dynamic optimization of human walking. J Biomech Eng 123: 381-390.
- K Iqbal, YC Pai (2000) Predicted region of stability for balance recovery motion at the knee joint can improve termination of forward movement. J Biomech 33: 1619-1627.
- LR Humphrey (2009) Modeling of the Foot, Toes and Vestibular System in Human Balance. The Ohio State University.
- LR Humphrey, H Hemami (2010) A computational human model for exploring the role of the feet in balance. J Biomech 43: 3199-3206.
- FJ Richmond, PP Vidal (1988) The motor system: Joints and muscles of the neck. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 1-21.
- J Baker, C Wickland (1988) Kinematic properties of the vestibulocollic reflex. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 167-177.
- J Winter (1988) Biomechanical modeling of the human neck and head. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 22-36.
- RD Rabbitt, ER Damiano, JW Grant (2004) Biomechanics of the semicircular canals and otolith organs. In: SM Highstein, RR Fay, AN Popper, The Vestibular System. Springer Verlag, 153-201.
- BW Peterson (1988) Cervicocollic and cervico-ocular reflexes. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 90-99.
- VJ Wilson, BW Peterson (1988) Vestibular and reticular projections to the neck. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 129-140.
- N Hirai (1988) Cerebellar pathways contributing to head movement. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 187-195.
- L Stark, WH Zangemeister, B Hannaford (1988) Head movement models, optimal control theory, and clinical application. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 245-260.
- VJ Wilson (1988) The tonic neck reflex: Spinal circuitry. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 100-107.
- O Pompeiano (1988) The tonic neck reflex: Supraspinal control. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 108-119.
- A Roucoux, M Crommerlinck (1988) Control of head movement during visual orientation. In: BW Peterson, FJ Richmond, Control of Head Movement. Oxford University Press, 208-223.
- AM Green, Y Hirata, HL Galiana, SM Highstein (2004) Motor learning in the VOR. In: SM Highstein, RR Fay, AN Popper, The Vestibular System. Springer Verlag, 423-495.
- GM Halmagyi, IS Curthoys, ST Aw, J Jen (2004) Clinical applications of basic vestibular research. In: SM Highstein, RR Fay, AN Popper, The Vestibular System. Springer Verlag, 496-546.
- JK Aggarwal (1972) Notes on Nonlinear Systems. In: D Van Nostrand co, (1st edn), New York.
- G Leitmann (1994) Lyapunov stability theory based control of uncertain dynamic systems. In: A Miele, A Salvatti, Applied Mathematics in Aerospace and Engineering. Plenum Press, New York, 281-292.
- RA Freeman, P Kokotovic (1996) Approches to robust nonlinear control. In: F Garofalo, L Glielmo, Robust Control via Variable Structure and Lyapunov techniques. Springer, 1-14.
- H Khalil (1996) Nonlinear Systems. Prentice Hall, New Jersey.
- H Hemami, V Utkin (2002) On the dynamics and Lyapunov stability of constrained and imbedded rigid bodies. International Journal of Control 75: 408-420.
- H Hemami, BF Wyman (2012) A simple strategy for jumping straight up. Math Biosci 237: 28-37.
- H Hemami, VI Utkin (2015) Postural stability on minimal support. In: F Miranda, Control Theory: Perspectives, Applications and Developments. Nova Science Publishers, 2015.
- J Wittenberg (1977) Dynamics of Systems of Rigid Bodies. BG Teubner.
- H Hemami, M Hemami (2014) Modeling and monitoring of passive control structures in human movement. International Journal of Control 87: 1861-1876.
- BW Bader, TG Kolda (2007) Efficient matlab computations with sparse and factored tensors. SIAM Journal on Scientific Computing 30: 205-231.
- H Hemami, B Dariush (2012) Central mechanisms for force and motion towards computational synthesis of human movement. Neural Netw 36: 167-178.
- A Pellionisz, R Llinas (1979) Brain modeling by tensor network theory and computer simulation. the cerebellum: distributed processor for predictive coordination. Neuroscience 4: 323-348.
- A Pellionisz, R Llinas (1980) Tensorial approach to the geometry of brain function: cerebellar coordination via a metric tensor. Neuroscience 5: 1125-1138.
- B Peterson (1995) Head movement: Multidimensional modeling. In: M Arbib, The Handbook of Brain Theory and Neural Networks. Mass: The MIT Press, Cambridge, 450-454.
- H Hemami, K Barin, YC Pai (2006) Quantitative analysis of a sagittal biped under platform disturbance. IEEE Trans Neural Syst Rehabil Eng 14: 470-480.
- J Dinneen, H Hemami (1993) Stability and movement of a one-link neuromusculo-skeletal sagittal arm. IEEE Trans Biomed Eng 40: 541-548.
- F Bullo, A Lewis (2005) Geometrical Control of Mechanical Systems. Springer.
- N Hogan (1984) Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Transactions on Automatic Control 29: 681-690.
- AI Mees (1981) Dynamics of Feedback Systems. In: John Wiley and Sons, (1st edn), Chichester.
- A Nambu (2004) A new dynamic model of the cortico-basal ganglia loop. In: S Mori, DG Stuart, M Wiesendanger, Brain Mechanisms for the Integration of Posture and Movement. Elsevier, 143: 461-466.
- H Hemami, ZM Moussavi (2014) A model of the basal ganglia in voluntary movement and postural reactions. Comput Methods Biomech Biomed Engin 17: 1432-1446.
- LB Rapoport (1996) Asymptotic stability and periodic motions of selector linear differential inclusions. In: F Garofalo, L Glielmo, Robust Control via Variable Structure and Lyapunov techniques. Springer, New York, 269-285.
- H Hemami, B KhosraviSichani, K Barin (2016) Airborne and landing phases of a simplified back somersault movement. Journal of Computers and Electrical Engineering 53: 1-12.
- F Anderson, M Pandy (1999) A dynamic optimization solution for vertical jumping in three dimensions. Comput Methods Biomech Biomed Engin 2: 201-231.
- JE Desmedt, E Godaux (1997) Ballistic contractions in man: characteristic recruitment pattern of single motor units of the tibialis anterior muscle. J Physiol 264: 673-693.
Author Details
Hooshang Hemami1 and Kamran Barin2*
1Department of Electrical and Computer Engineering, The Ohio State University, USA
2Department of Otolaryngology, The Ohio State University, USA
Corresponding author
Kamran Barin, Department of Otolaryngology, The Ohio State University, Columbus, Ohio, 43210, USA, E-mail: [email protected]
Accepted: April 04, 2017 | Published Online: April 07, 2017
Citation: Hemami H, Barin K (2017) Preliminary Design of a Generalized Vestibular Sensory System. Int J Astronaut Aeronautical Eng 2:003.
Copyright: © 2017 Hemami H, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A rudimentary vestibular system as a single sensory system for a multi-rigid body system is proposed. The semi-circular canals represent the main sensors for the state of the physical system, and are modeled as accelerometers. Their outputs are used to estimate the angular velocities and positions of the multi-rigid body system. The states and the accelerations are utilized in feedback and feed forward control paths for movements on the ground and in the air. The sensory system is implemented in a three-dimensional system that corresponds roughly to a human foot, leg, thigh and torso. Computer simulations are carried out to assess the feasibility and performance of this vestibular sensory system.
Keywords
Sensory system, Vestibular sensors, Semi-circular canals, Vestibular signal processing, Estimating angular acceleration, Velocity and position
Introduction
Recent artificial vestibular sensors [1-3] mandate the need for more comprehensive study of the vestibular machinery in humans and animals [4-7].
The anatomical and muscular structures [8-10] must eventually be integrated in such sensory systems for robotic and rehabilitation purposes, including better models of support as provided by the feet [11-13]. The vestibular apparatus [14-17], the machinery for [18,19] and processing [20,21] as well as all the different functions of the vestibular system, (e.g, tonic reflexes [15,22,23], visual orientation [15,24], motor learning [25], other reflexes [18], etc.) are all challenging scientific, medical [26], rehabilitation oriented and physiological issues. For simplicity, we develop a basic sensory system and use it primarily in stability studies. This effort should lead to more anatomically realistic studies [4-7]. We add a redundant Lyapunov function [27] for monitoring stability. The construction of an energy Lyapunov function (analogous to the construction of such functions for linear stable time-invariant systems [28-30] is adopted here. The energy function is relatively easy to construct for the unconnected rigid bodies. The Lyapunov function for the connected multi rigid body system is the projection of the Lyapunov function for the corresponding free-rigid-body system [31]. A comprehensive Lyapunov function allows integration of all reflexes of the head and neck movement and a calibrated analysis of all these reflexes.
The states of the system that are used for stability, control and feedback play a crucial role and have to be available at all times. Therefore, the availability of the states dictates the choice of the sensory system and the needed processing. The human vestibular system estimates the head's states of position and velocity. The process is to measure angular accelerations and derive the velocities and positions by a double integration process in time. The individual rigid bodies of the multi-link system must be equipped with vestibular apparatus for estimation of their states. The states become important parts of the development. The dynamics proposed here are the Newton-Euler formulation [32,33]. When Lagrangian dynamics or other generalized coordinate systems are preferred, additional processing is needed to estimate positions, velocities and accelerations for the dynamics of choice.
For the sensory system developed here, one needs three coordinate systems: the inertial coordinate system (ICS), the body coordinate system (BCS) and the vestibular coordinate system (VCS). Bryant angles [34] define the position state variables. The angular velocity of every rigid body in its own principal axes coordinate system (BCS) is the velocity state variable [33,35]. Tangential accelerations are used for inertial control purposes. A simple four-link biped is considered here with the two feet as one rigid body, the two legs and the two thighs as two rigid bodies, and the torso as the fourth rigid body.
In the present formulation, the accelerations are integrated twice to arrive at the velocity and position states. The integrators need initial conditions and values to perform accurately. In the human system, the needed information comes from the otolith organs, and the vision and proprioceptive systems [5,24]. The inclusion of otolith function, proprioceptive sensing and role of vision in the present formulation merits further research and is not further addressed here.
Two versions of the accelerometer-based sensory system and their required processing are presented in Section Two. The dynamics of the four-rigid-body system with 12 pairs of muscle-like actuators are briefly presented in Section Three. Computer simulations of the system with and without passive connecting ligaments and cartilages are presented in Section Four. Discussions and conclusions are presented in Section Five. Appendices and References follow.
Sensory System Models
The two sensory systems presented below are based on the Newton-Euler formulation of the multi-link system and a generalized version of the vestibular system. All rigid bodies of the system are equipped with the same system of sensors that measure rotational and linear accelerations from which angular velocities and positions are induced by processing the accelerometer signals.
There is redundancy in the sensors. Three pairs of sensors are available for each rigid body in the first sensory system. Consequently, there is an economy in computation and processing. The second sensory system is based on one pair of sensors as in the human head. As a result, it requires more elaborate computation and processing.
Redundant sensory system
First, the coordinate systems are introduced. The ICS system's three orthogonal axes are to the front, left and vertically upward-a right-hand coordinate system. The BCS system of the head has the coordinate system: forward, right to left, and upwards. It is assumed that the principal axes of the head are along the same three-axes of the coordinate system of the head: front, left to right, and vertical. This assumption positions the semicircular canals on the second principal axis. The third coordinate system is defined by the semicircular canals [36].
A position in or on the head is specified by its three fixed coordinates in the BCS system. The same point, as the head moves, is specified by -the three Bryant angles [34] relative to the ICS system). A linear three-by-three matrix A transforms vectors in the BCS to vectors in the ICS.
Suppose a rigid body's center of gravity (COG) is fixed at the origin of ICS and the rigid body rotates about its COG with angular velocity . Let a point i have coordinate vectors Xi and Qi, respectively, in ICS and BCS. In the following equation, i refers to point 1, 2 or 3. The position variables in the ICS and BCS are related by
The transformation A(¬) and ¬ can be derived from
The velocity of point i (in ICS) is given by [34]
where is the anti-symmetric three-by-three matrix of . The acceleration sensed at a point i, is given by:
Assume a three-dimensional accelerometer is installed at point i and its axes are parallel to the principal axes of the rigid body in BCS. The accelerometer measures the three components . This equation provide information about and . The vector output of? the accelerometer, i.e., the sensed three values, provide information about and . The measured acceleration vector has to be integrated with respect to time in order to derive the vector velocity . Consequently, becomes available for inertial feedback purposes' and for velocity feedback.
More accelerometer sensors simplify and speed up the processing and estimation efforts. Consider for now only a one-segment rigid-body system. The equations equally apply to multi-rigid-body systems.
Suppose all segments of a human body, a humanoid, or robots are equipped with multi-sensors, as follows. Consider six three-dimensional accelerometers, installed symmetrically on the principal axes of the rigid body, respectively, at positions Q1, Q-1, Q2, Q-2, Q3 and Q-3. Let the same vectors be, respectively, designated by Xi and X(-i) with i = 1,2,3 in the ICS system (Figure 1). These accelerometers can be installed at other locations as long as they are not installed in the same plane, but the processing and computations may become more substantial.
Let Xh be the coordinates of the rigid body COG in ICS. The positions, velocities and accelerations of the pair of accelerometers expressed, in the ICS, are
It is shown below how the signals in Equation 5 are processed to estimate the state of the rigid body and the derivative of the state with respect to time. The estimates are adequate to supply feed-forward and feedback paths with states and acceleration information.
Signal processing
Addition and subtraction of symmetric pairs of accelerometer outputs, velocities and positions provide complete separate information about the translation and rotation of the rigid body (or the head).
For the translational motion:
Let
qq = [q1,q2,q3]
and
pp = [p1.p2,p3].
From the sensed accelerometer measurements, matrix A can be derived:
From the computed matrix A , the angles can be derived [34]. The angular velocities can be similarly derived.
From the measured acceleration terms in Equation 6, the angular acceleration terms can be inferred from as in Equation 8.
Finally, if the dynamics are formulated by the Lagrangian method is arrived at from
The tangential component of at vector position R is arrived by the inner product of Equation 9 with vector
One Pair of Accelerometers
Based on the definitions of the VCS, we consider two geometrical arrangements for the three canals. Consider the right ear with its location specified by vector Qr. The anterior SCC is such that the vertical plane xz is rotated clockwise by 45 degrees. The posterior SCC is such that the vertical yz plane is rotated counterclockwise by 45 degrees. Finally the horizontal SCC is situated by a clockwise rotation of 30 degrees about the y axis from the horizontal xz position. This coordinate system is more precisely formulated as a transformation of Bryant angles of the head (in BCS) by
The transformation from BCS to the above VCS is given by the matrix ABV 1
Consider a second transformation ABV 2 with
These two transformations allow accelerations, sensed in the VCS by the right and left canals, to be converted to tangential accelerations in the BCS. The inversion can be carried out by neural populations as described in [37] which amounted to inversion of a three-by-three matrix H3 with four non-zero elements. If the matrices to be inverted are larger, computationally oriented tensor strategies may be needed [38-40]. We will not consider such cases in this paper.
When the outputs of the accelerometers are added together, the resulting transformation matrix is the sum of the above two transformations, where three of the non-diagonal elements become zero. Consequently, the inversion of the resulting matrix is easier [37,41]. Suppose there are only two three-dimensional accelerometers located at +Q and -Q on the head as shown in Figure 1. Let the accelerometers be located along the y-axis (the right and left direction as on the human head.) It is assumed that the three accelerometers measure the acceleration, just as the semi-circular canals do in VCS.
The objective is to estimate translational and rotational position and velocity states from the output of these two accelerometers. More linear transformations of the signals could be undertaken to include transfer functions for the behavior of individual canals [17]. The translation velocity estimator is just the integrator of the acceleration of the COG in the ICS system. The position is the result of the integration of the velocity of the COG in the ICS system. The acceleration of the head COG is derived by addition of the equations in Equation 6.
For the rotational acceleration, one subtracts acceleration terms in Equation 5.
The resulting transformation amounts to adding the above two matrices together ABV 1 + ABV 2. This matrix can be written as a product of two matrices: a diagonal matrix and an orthonormal matrix. Both are easy to invert. The first requires inversion of three scalers. For the second one, the transpose of the matrix is the inverse. We consider Equation 13 for a simple case: rotation in the sagittal plane as in a back somersault. In this case the vector and Q2 are along the body's y axis and hence their outer product in Equation 13 is equal to zero. Two equations govern the structure of the rotational estimator [32]:
From the above two equations, the structure of the estimator can be inferred.
Four-link System
The four-link biped equations can be derived from the free-body diagrams of four rigid bodies [32]. The inertial axes are front, left and vertical upward. The rotations about these axes are, for easy visualization, roll, pitch and yaw as they apply to an airplane. The system equations can be seen in [32]. The bodies are supposed to be connected together at one point as shown in Figure 2. Each connection is described by three holonomic constraints.
Two cases are considered. If the contact area with the ground is adequate, such as the case of support by the normal human foot, sufficient torque is available at the joint with the ground. If the system is on tiptoe, no torque is available at the ground joint and the system is under-actuated. As shown in [32] the system is reduced to 12 attitudinal degrees of freedom by elimination of the translational degrees of freedom.
At the four joints, we assume three pairs of actuators control the relative movement between the three degrees of freedom. We assume all actuators function similarly and all have the same moment arm that, for simplicity, is assumed to be unity. Every actuator is driven by tension that stretches the tendon linearly [41,42]. As a result, linear feedback of the position and velocity [43] is possible by co-activation. Feeding forward of central signals takes place with the same gains. The central input signals in our case are simple periodic trajectories of the angles (roll and pitch). The velocity feedback, a consequence of actuator dynamics and viscosity, is supposed to be linear and a fraction of the gains for position feedback. The dynamics of the 12-dimensional system are symbolically written as
The inputs to the system are the moment of force vectors Nr of dimension 12 in the above equation. Part of Nr is the linear feedback of position states and velocities due to muscular co-activation [44]. Second components of the input torques are periodic inputs from the central controller or, in the human system, signals that are issued from the CNS that energize the agonist muscles and by which the periodic movement of all the segments (self rotation) is implemented. A third component is the connection and support forces of ligaments and cartilages as the passive component. The vector Nr has three components at every joint. N1 is at the ground joint. N2 is at the ankle joint. N3 is at the knee joint, and N4 is at the hip joint.
The above system does not have acceleration feedback. However, for somersault movements, inertial adjustments require acceleration feedback.
Computer Experiments
In order to test the sensory system proposed here, postural stability of the four-link system when on tiptoe (i.e., when the ground joint torque is zero) is simulated. The strategy is to rotate the segments about the vertical axes [45] by providing reference inputs to the four-link system as follows.
• The central controller produces simple stable reference oscillations with appropriate phases.
• There are direct paths to the spinal cord (or the actuators) for the references.
• The gains of all the actuators are centrally set and controlled in the basal ganglia as discussed in [46,47].
Two cases are considered here.
Case 1. The toe torque N1 is small.
Case 2. The toe torque is zero.
N1 = 0.
In the simulation, the passive structures and the active muscular structure control the behavior of the system in a postural stability experiment [32,33]. There are four rigid bodies held together by ligaments and cartilage. These passive structures keep the connection constraints between the four segments. The masses of the four segments, in kilograms, are [2, 6, 16, 46]. The joint cartilage and ligaments are modeled as linear elements with constant viscosity. The joint stiffness, in Newton's per centimeter, is selected such that every joint has a one centimeter compression due to gravity: K = [70000, 68000, 62000, 46000]. The viscosity is assumed to be about half of the stiffness. The actuators are also linear with gains of [500, 300, 300, 300] for the four joints in the sagittal plane, frontal plane and medial planes. First, stability is verified by testing the system in a transient mode.
Transient postural stability
The first experiment involves simulation of a transient behavior of the four-link system near the vertical stance. The initial pitch angles of the four segments are:
There are no central inputs or external disturbances. The 48 dimensional system remains stable. The behavior of the four Bryant angles in the sagittal plane is shown in Figure 3.
The energy of the system is used as a Lyapunov function [35]. The Lyapunov function, its derivative and the phase plane trajectory of the Lyapunov function are shown in Figure 4.
Cartilage compression
For this case, passive structures are included in the dynamics. The simulated system has all 48 degrees of freedom of the four rigid bodies. In this experiment the behavior of a linear combined cartilage and ligament model is studied.
The loading of the cartilages at the four joints are shown in Figure 5 as functions of time. Figure 6 shows the velocities of the compression as functions of time-every joint has a one-centimeter compression in this simulation.
Combined passive and active structures
In this simulation, the passive structures and the active muscular structure control the behavior of the system in a postural stability experiment [32,35]. The four rigid bodies are held together by ligaments and cartilage. These passive structures keep the connection constraints between the four segments. The system is excited by central inputs issued from stable Van der Pol oscillators [30,48] that excite the actuators at every joint in the frontal and sagittal planes, producing stable limit cycles.
The behavior of the system is shown in three Figure 6, Figure 7 and Figure 8. Figure 6 shows the velocities of the compression as functions of time. Every joint has a one-centimeter compression in this simulation.
The motion of the centers of gravity of the foot and the leg are shown in Figure 7. The centers of gravity follow a roughly circular stable trajectory. The cyclic motion of the center of gravity of the torso as functions of time and space are shown in Figure 8.
The simulations also show that, without the support on the ground (as a ballerina on tiptoe), the same three oscillator inputs maintain the four-link system's postural stability. More relevant computer simulations can be found in reference [49] where the control issues for a simple back somersault maneuver are addressed.
Discussion and Conclusions
Two new sensory systems that expand and generalize the vestibular sensors are introduced and designed here. One system is rich in sensors and does not require much processing. The second system has a minimal number of sensors-adequate for measuring the rotational and linear accelerations from which the states have to be estimated by computations We have formulated the dynamics of a three-dimensional, four-segment skeletal system with a new sensory system that is amenable to computer implementation and robotic applications. It has potential in vestibular and other sensory rehabilitation applications. The system here could be made more anatomically realistic by adding better physiological models [50,51] and by inclusion of higher-level human CNS strategies.
Two models of the sensory system were considered: one with more hardware and one with more computations and processing. In the dynamics here, passive structures that impose joint constraints and a system without passive constraints are simulated.
A three-segment head and neck model can be added to the present four-link model that enables inclusion of the vestibular apparatus, the signal processing, and the neural processing and integration of the vestibular signals in the VOR and spinal processing. The computational model may augment current experimental and clinical protocols in diagnosis, rehabilitation and monitoring of the recovery phases.
The vestibular apparatus formulated here may also find immediate applications in construction of artificial vestibular systems for replacement of the natural components that are damaged, diseased or injured. It also may help in the synthesis of components that must interface the artificial components with the nervous system. The formulation relies mainly on matrices and can be expanded to larger dimensional rigid-body systems with more complex joints. With the above results as motivation, one may wish to explore human brain oscillators and structures that produce the desired periodic inputs with proper phase shifts for the desired limit cycle stability. The same structures may also be involved in dancing and coordinated rhythmic movement.
Such sensory systems also could find applications in the design of artificial muscles where the artificial muscle does not have to contain sensory elements of its own (as in natural systems). Consequently, the designs would be simpler. However, because of the lack of fast muscular reflexes, such a system would only accommodate slow movements.
Acknowledgment
The authors are very grateful to Professor Joel Johnson, Chair of Electrical and Computer Engineering of The Ohio State University, for support of this work. The authors acknowledge the assistance of Edwin Lim of the Computer Facilities of the Department of Electrical and Computer Engineering of The Ohio State University. The authors are grateful to the reviewers for valuable comments and criticism, and to David B. Ball for editorial assistance.
Appendices
Appendix A, lyapunov function
The Lyapunov energy function is constructed here as a sum of four functions. The elastic muscular energy is v1 [31]. The rotational kinetic energy is v2. The kinetic energy of translation is v3, and the potential energy is v4.X_i0 is the initial or equilibrium value of vector X_i.
Appendix B, physical parameters
The physical parameters of the system are given in Table 1.

